目录
一、说明
二、无策略直接匹配法
2.1 简单粗暴的无脑匹配:
2.2 跳过外循环的思路
2.3 跳过内循环的思路
2.4 KMP算法时间分析
三、KMP有限状态机
四、结论
一、说明
KMP算法问题:给定一个(短)模式和一个(长)文本,这两个都是字符串,确定该模式是否出现在文本中的某处。上次我们看到了如何使用有限自动机来做到这一点。这次我们将介绍 Knuth-Morris-Pratt (KMP) 算法,它可以被认为是构建这些自动机的有效方法。
Knuth-Morris-Pratt 字符串匹配:见【NLP】KMP匹配算法_无水先生的博客-CSDN博客
二、无策略直接匹配法
首先让我们看一个没策略的简单的解决方案。
- 假设文本在一个数组中:char T[n]
- 模式在另一个数组中:char P[m]。
一种简单的方法就是尝试该模式可能出现在文本中的每个可能位置。
2.1 简单粗暴的无脑匹配:
for (i=0; T[i] != '\0'; i++)
{
for (j=0; T[i+j] != '\0' && P[j] != '\0' && T[i+j]==P[j]; j++) ;
if (P[j] == '\0') found a match
}
有两个嵌套循环;内部的需要 O(m) 次迭代,外部的需要 O(n) 次迭代,所以总时间是乘积 O(mn)。这很慢;我们想加快速度。
在实践中,这工作得很好——通常不像这个 O(mn) 最坏情况分析那么糟糕。这是因为内层循环通常会很快发现不匹配并移动到下一个位置,而无需经过所有 m 个步骤。但是这种方法对于某些输入仍然可以采用 O(mn)。在一个不好的例子中,T[] 中的所有字符都是“a”,而 P[] 除了末尾的一个“b”之外都是“a”。然后每次都要进行 m 次比较才能发现你没有匹配,所以总的来说是 mn 次。
这是一个更典型的例子。每行代表外循环的一次迭代,行中的每个字符代表比较的结果(如果比较不相等则为 X)。假设我们要在文本“banananobano”中寻找模式“nano”。
0 1 2 3 4 5 6 7 8 9 10 11
T: b a n a n a n o b a n o
i=0: X
i=1: X
i=2: n a n X
i=3: X
i=4: n a n o
i=5: X
i=6: n X
i=7: X
i=8: X
i=9: n X
i=10: X
其中一些比较是无用功!例如,在迭代 i=2 之后,我们从已经完成的比较中得知 T[3]="a",因此在迭代 i=3 中将它与 "n" 进行比较是没有意义的。而且我们也知道 T[4]="n",所以在迭代 i=4 中进行相同的比较是没有意义的。
2.2 跳过外循环的思路
Knuth-Morris-Pratt 的想法是,在这种情况下,在你投入大量工作对代码的内部循环进行比较之后,你就会对文本中的内容了解很多。具体来说,如果您找到了从位置 i 开始的 j 个字符的部分匹配,您就会知道位置 T[i]...T[i+j-1] 中的内容。
您可以使用这些知识以两种方式节省工作。首先,您可以跳过一些无法匹配的迭代。尝试将找到的部分匹配项与要查找的新匹配项重叠:
i=2: n a n
i=3: n a n o
这里模式的两个位置相互冲突——我们从 i=2 迭代中知道 T[3] 和 T[4] 是“a”和“n”,所以它们不可能是“n”和 i=3 迭代正在寻找的“a”。我们可以不断跳过位置,直到找到一个不冲突的位置:
i=2: n a n
i=4: n a n o
这里两个“n”是重合的。将两个字符串 x 和 y 的重叠定义为作为 x 的后缀和 y 的前缀的最长单词。这里“nan”和“nano”的重叠只是“n”。 (我们不允许重叠全部是 x 或 y,所以它不是“nan”)。通常,我们要跳转到的 i 的值是与当前部分匹配的最大重叠对应的值:
具有跳过迭代的字符串匹配:
i=0;
while (i<n)
{
for (j=0; T[i+j] != '\0' && P[j] != '\0' && T[i+j]==P[j]; j++) ;
if (P[j] == '\0') found a match;
i = i + max(1, j-overlap(P[0..j-1],P[0..m]));
}
2.3 跳过内循环的思路
一个可以做的优化是跳过内循环中的一些迭代。让我们看一下同一个例子,其中我们从 i=2 跳到 i=4:
i=2: n a n
i=4: n a n o
在此示例中,重叠的“n”已通过 i=2 迭代进行了测试。无需在 i=4 迭代中再次测试它。一般来说,如果我们与最后的部分匹配有重要的重叠,我们可以避免测试与重叠长度相等的字符数。
此更改会产生(一个新版本的)KMP 算法:
KMP, version 1:
i=0;
o=0;
while (i<n)
{
for (j=o; T[i+j] != '\0' && P[j] != '\0' && T[i+j]==P[j]; j++) ;
if (P[j] == '\0') found a match;
o = overlap(P[0..j-1],P[0..m]);
i = i + max(1, j-o);
}
唯一剩下的细节是如何计算重叠函数。这只是 j 的函数,而不是 T[] 中字符的函数,因此我们可以在进入算法的这一部分之前在预处理阶段计算一次。首先让我们看看这个算法有多快。
2.4 KMP算法时间分析
我们还有一个外循环和一个内循环,所以看起来时间可能仍然是 O(mn)。但是我们可以用不同的方式来计算它,看看它实际上总是小于那个。这个想法是,每次通过内循环,我们都做一次比较 T[i+j]==P[j]。我们可以通过计算我们执行了多少次比较来计算算法的总时间。
我们将比较分为两组:返回 true 的和返回 false 的。如果比较返回真,我们就确定了 T[i+j] 的值。然后在未来的迭代中,只要存在涉及 T[i+j] 的非平凡重叠,我们就会跳过该重叠并且不再与该位置进行比较。所以T[]的每个位置只涉及一次真正的比较,总共可以有n次这样的比较。另一方面,外循环的每次迭代最多有一个错误比较,因此也只能有 n 个。结果我们看到 KMP 算法的这一部分最多进行 2n 次比较并且花费时间 O(n)。
三、KMP有限状态机
如果我们只看上面算法中 j 发生了什么,它有点像有限自动机。在每个步骤中,j 被设置为 j+1(在内部循环中,在匹配之后)或重叠 o(在不匹配之后)。在每一步中,o 的值只是 j 的函数,并不依赖于其他信息,例如 T[] 中的字符。所以我们可以画出类似自动机的东西,用箭头连接 j 的值并用匹配和不匹配标记。
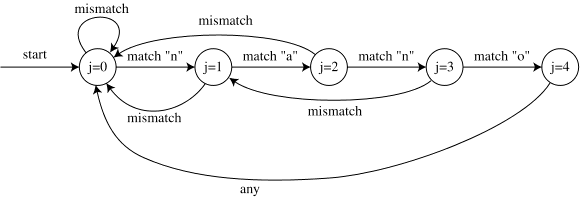
这和我们习惯的自动机之间的区别在于它每个圆圈只有两个箭头,而不是每个字符一个。但是我们仍然可以像任何其他自动机一样模拟它,方法是在开始状态 (j=0) 上放置一个标记并围绕箭头移动它。每当我们在 T[] 中找到一个匹配的字符时,我们就会继续处理文本的下一个字符。但是每当我们遇到不匹配时,我们在下一步中查看相同的字符,除了状态 j = 0 中的不匹配情况。
所以在这个例子中(与上面的例子相同)自动机经历了状态序列:
j=0
mismatch T[0] != "n"
j=0
mismatch T[1] != "n"
j=0
match T[2] == "n"
j=1
match T[3] == "a"
j=2
match T[4] == "n"
j=3
mismatch T[5] != "o"
j=1
match T[5] == "a"
j=2
match T[6] == "n"
j=3
match T[7] == "o"
j=4
found match
j=0
mismatch T[8] != "n"
j=0
mismatch T[9] != "n"
j=0
match T[10] == "n"
j=1
mismatch T[11] != "a"
j=0
mismatch T[11] != "n"
这基本上与上面的 KMP 伪代码完成的比较序列相同。所以这个自动机提供了 KMP 算法的等价定义。
有个疑问点,该自动机中可能不清楚的一个转换是从 j=4 到 j=0 的转换。一般来说,应该有从 j=m 到某个较小的 j 值的转换,这应该发生在任何字符上(在进行此转换之前没有更多的匹配项要测试)。如果我们想找到模式的所有出现,我们应该能够找到一个出现,即使它与另一个重叠。因此,例如,如果模式是“nana”,我们应该在文本“nanana”中找到它的两次出现。因此,从 j=m 的过渡应该转到下一个可以匹配的最长位置,即 j=overlap(pattern,pattern)。在这种情况下,overlap("nano","nano") 为空(“nano”的所有后缀都使用字母“o”,没有前缀)所以我们转到 j=0。
四、结论
基于自动机模型,将模式一次性扫描自动构成自动机模型,这是有意义的。如果给出一个模式,设计一套自动机,这种实用性不足。看来研究一个随生成限状态机是必要的。