Leetcode | 39 组合总和

题目

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates = [2], target = 1
输出: []

提示：

• 1 <= candidates.length <= 30
• 2 <= candidates[i] <= 40
• candidates 的所有元素 互不相同
• 1 <= target <= 40

我的思路

首先，这题肯定得用回溯或者递归，因为每个数都可以重复。

其次，处理当前数的时候，最多可以重复count = target / cur_num 遍，不管能不能整除。因此对count进行遍历，然后对剩余的候选者进行同样的操作，直至剩余的target 为 0。

class Solution {
public:
    void Push2Vector(vector<vector<int>>& targets, vector<int>& vec) {
        for(auto &vec_tar : targets) {
            if(vec_tar.size() == vec.size()){
                bool existed = true;
                for(int i = 0; i < vec_tar.size(); ++i) {
                    if(vec_tar[i] != vec[i]) {
                        existed = false;
                        break;
                    }
                }
                if (existed) {
                    return;
                }
            }
        }
        targets.push_back(vec);
        return;
    }

    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector<vector<int>> ret;
        
        bool same = false;
        int num_size = candidates.size();
        if(num_size == 1 && candidates[0] > target) {
            return {};
        }


        for(int i = 0; i < num_size; ++i) {
            int num = candidates[i];
            vector<int> match;
            if(num > target) {
                continue;
            } else if (num == target && !same) {
                match.push_back(num);
                Push2Vector(ret, match);
                same = true;
            }

            int count = target / num;
            while(count > 0) {
                vector<vector<int>> ret1 = combinationSum(candidates, target - count * num);
                vector<int> ret2;

                for(int j = 0; j < ret1.size(); ++j) {
                    for(int k = 0; k < count; ++k) {
                        ret1[j].push_back(num);
                    }
                    sort(ret1[j].begin(), ret1[j].end());
                    Push2Vector(ret, ret1[j]);
                }
                --count;
            }


        }
        return ret;
    }
};

这种算法最大的问题就是遍历的太多，耗时太大。

官方题解

回到本题，我们定义递归函数 dfs(vector<int>& candidates, int target,vector<vector<int>> &ret, vector<int>& combine, int idx)表示当前在 candidates 数组的第 idx\textit{idx}idx 位，还剩 target 要组合，已经组合的列表为 combine。

递归的终止条件为 $target≤0 $ 或者 candidates数组被全部用完。那么在当前的函数中，每次我们可以选择跳过不用第 idx个数，即执行 $dfs(target,combine,idx+1)$。也可以选择使用第 idx 个数，即执行 dfs(target−candidates[idx],combine,idx)，注意到每个数字可以被无限制重复选取，因此搜索的下标仍为 idx。

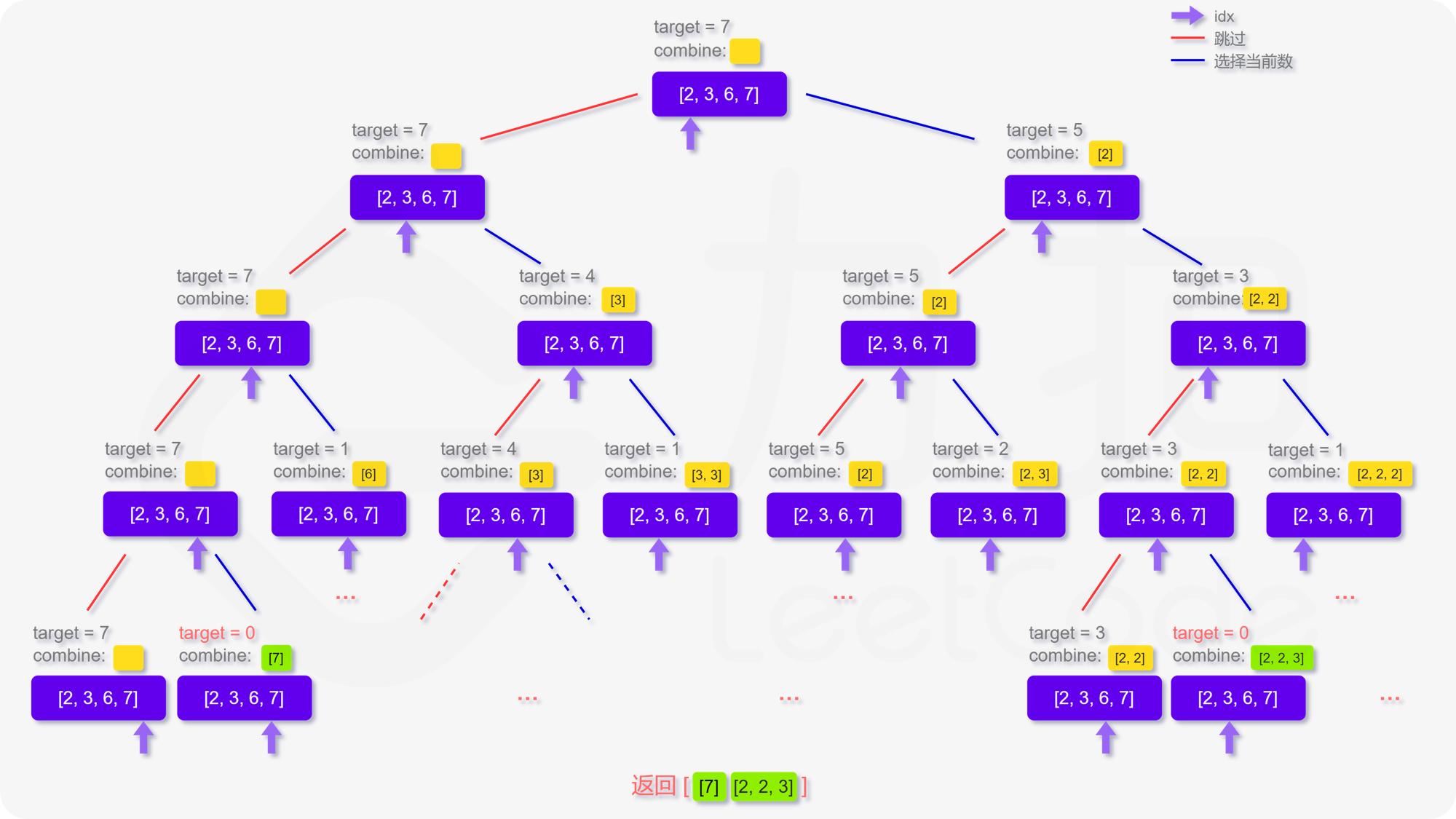
概况起来就是，每个数字都有2种选择，因此每个dfs函数中会再进行2次dfs，每次dfs之前判断终止条件即可。

class Solution {
public:
    void dfs(vector<int>& candidates, int target,vector<vector<int>> &ret, vector<int>& combine, int idx) {
        if(idx == candidates.size()) {
            return;
        }

        if(target == 0) {
            ret.emplace_back(combine);
            return;
        }

        // 直接跳过当前数
        dfs(candidates, target, ret, combine, idx + 1);

        // 当前数不跳过
        if(target - candidates[idx] >= 0) {
            combine.emplace_back(candidates[idx]);
            dfs(candidates, target - candidates[idx], ret, combine, idx);
            combine.pop_back(); // 这里pop_back 为了在dfs各路return的链路上进行清空！
        }
    }


    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector<vector<int>> ret;
        vector<int> combine;
        dfs(candidates, target, ret, combine, 0);
        return ret;
    }
};

作者：力扣官方题解
链接：https://leetcode.cn/problems/combination-sum/solutions/406516/zu-he-zong-he-by-leetcode-solution/

---

欢迎关注公众号【三戒纪元】