图论的概念:图论是数学的一个分支,它是以图为研究对象,图论中的图是由若干个给定的点及连接两点的线所构成的图形,这种图形通常用来描述某些实体之间的某种特定的关系,用点代表实体,用连接两点之间的线表示两个实体之间具有某种关系。
图的分类:
- 无权无向图
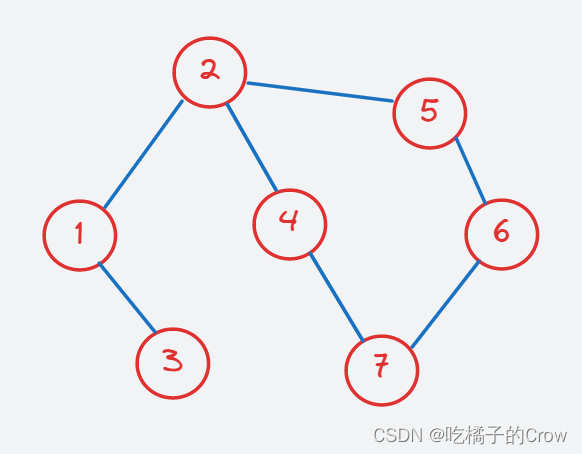
无向就是可以互相通向,没有进行方向的限制,就好比双向指向:

- 无权有向图

无权就是好比每条路线占的权重一致,没有区别,故我们可以把无权图假设为每个权重都是1的有权图:
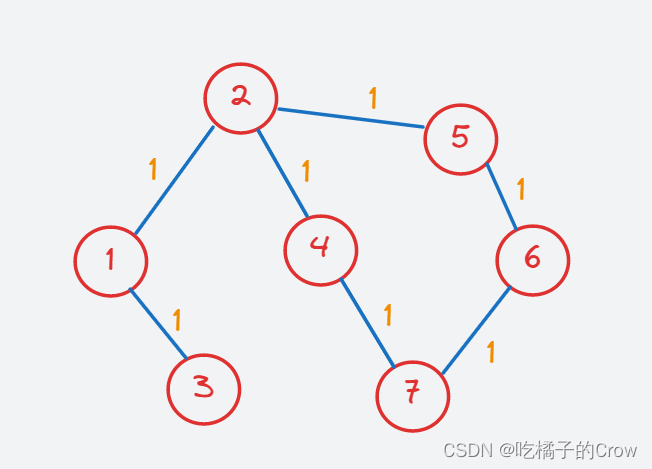
- 有权无向图

- 有权有向图
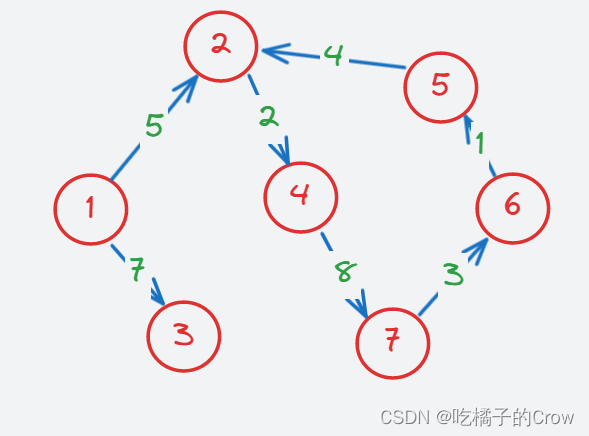
BFS和DFS
我们首先来了解什么是BFS?什么又是DFS?
DFS俗称深度优先算法,有一种不撞南墙不回头的感觉,认准一条路,一致往下走,直到走不通位置,然后再重新返回再重复刚才的操作,直到找到目标节点为止。DFS关键点是递归以及回溯,一般用栈进行操作。在图中我们经常这样:
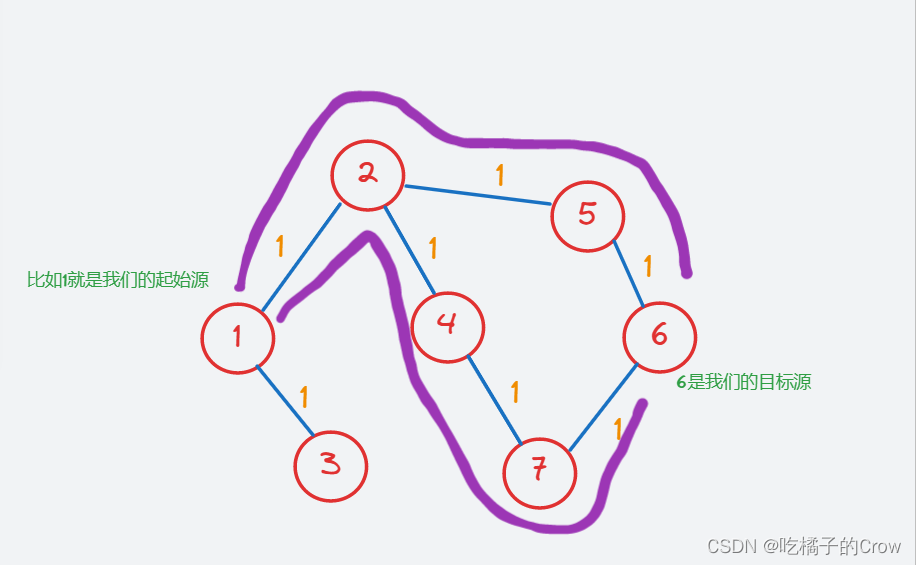

BFS俗称广度优先算法,相对于深度优先算法,如果把深度优先算法当成是一个莽夫的话,广度优先算法像是一个文人墨客,广度优先算法在面临一个路口时,把所有的路口记录下来,然后选择其中一个进入,然后再回退再进入另一个路口,直到找到目标节点为止。BFS关键点是状态的选取和标记,一般用队列去解决问题,在图中我们经常这样:

图的存储结构
- 邻接矩阵
概念:所谓邻接矩阵存储结构就是每个顶点用一个一维数组存储边的信息,这样所有点合起来就是用矩阵表示图中各顶点之间的邻接关系。所谓矩阵其实就是二维数组。对于有n个顶点的图 G=(V,E) 来说,我们可以用一个 n× n 的矩阵A来表示G中各顶点的相邻关系
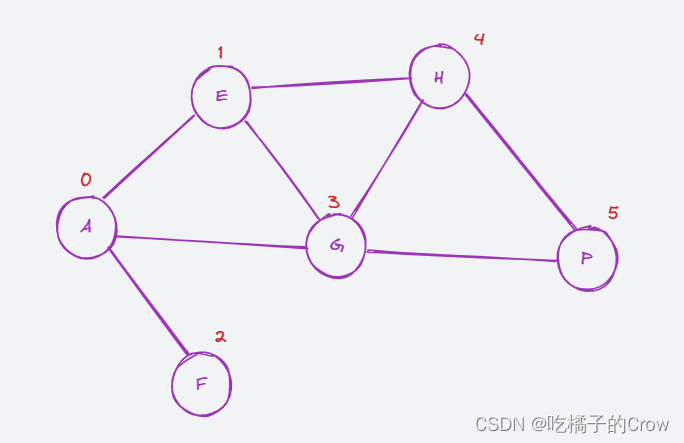
对应的邻接矩阵为:
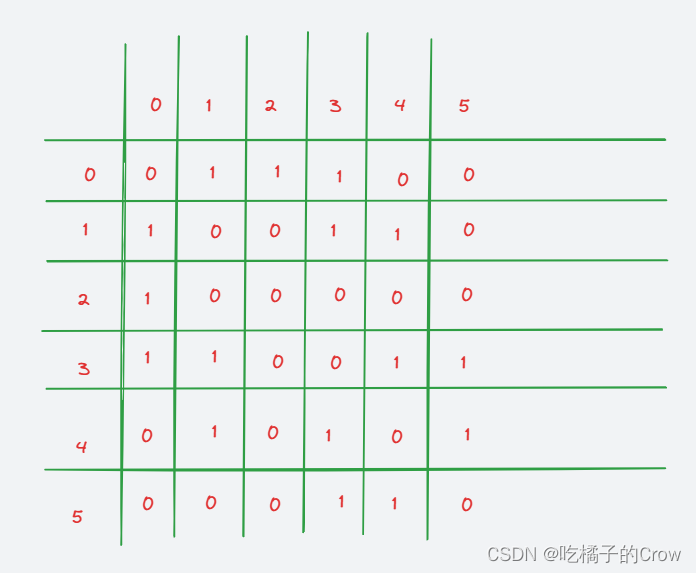
与对应点直接相连为1,不直接相连为0
构建邻接矩阵:
package graphtheory;
import java.util.Arrays;
/**
* 图的表示--使用邻接矩阵
*/
public class Graph01 {
private char[] V;//顶点上的值
private Vertex[] vertexs;//顶点数组
private int N;
//邻接矩阵
private int[][] adj;
//图的构造函数
public Graph01(char[] arr) {//{'A','E','F','G','H','P'}
//拿到数组的长度
int length = arr.length;
this.N = length;
V = new char[length];
//arr元素赋值 到V
this.V = Arrays.copyOf(arr, length);
//构建图中的结点
vertexs = new Vertex[length];
for (int i = 0; i < length; i++) {
vertexs[i] = new Vertex(i,this.V[i]);//
}
this.adj = new int[length][length];
}
//打印邻接矩阵
public void show() {
System.out.print(" ");
for (int i = 0; i < this.N; i++) {
System.out.format("%4c", this.V[i]);
}
System.out.println();
for (int i = 0; i < this.N; i++) {
System.out.format("%4c",this.V[i]);
for (int j = 0; j < this.N; j++) {
System.out.format("%4s", this.adj[i][j] > 0?(this.adj[i][j]):"-");
}
System.out.println();
}
}
/**
* 创建顶点类
*/
private class Vertex {
char v;//值
int index;//索引
public Vertex(int index, char c) {
this.index = index;
this.v = v;
}
}
public static void main(String[] args) {
char arr[] = {'A', 'E', 'F', 'G', 'H', 'P'};
//构建graph01
Graph01 graph01 = new Graph01(arr);
//进行连接
int[][] adjMatrix = graph01.adj;
adjMatrix[0][1]=1;
adjMatrix[0][2]=1;
adjMatrix[0][3]=1;
adjMatrix[1][0]=1;
adjMatrix[1][3]=1;
adjMatrix[1][4]=1;
adjMatrix[2][0]=1;
adjMatrix[3][0]=1;
adjMatrix[3][1]=1;
adjMatrix[3][4]=1;
adjMatrix[3][5]=1;
adjMatrix[4][1]=1;
adjMatrix[4][3]=1;
adjMatrix[4][5]=1;
adjMatrix[5][3]=1;
adjMatrix[5][4]=1;
graph01.show();
}
}

- 邻接表
邻接表的概念:邻接表的思想是,对于图中的每一个顶点,用一个数组来记录这个点和哪些点相连。由于相邻的点会动态的添加,所以对于每个点,我们需要用List来记录。

对应的邻接表为:

package graphtheory;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
/**
* 图的表示--使用邻接矩阵
*/
public class Graph02 {
private char[] V;//顶点上的值
private Vertex[] vertexs;//顶点数组
private int N;
//邻接矩阵
private List<Integer>[] adj;
//图的构造函数
public Graph02(char[] arr) {//{'A','E','F','G','H','P'}
//拿到数组的长度
int length = arr.length;
this.N = length;
V = new char[length];
//arr元素赋值 到V
this.V = Arrays.copyOf(arr, length);
//构建图中的结点
vertexs = new Vertex[length];
for (int i = 0; i < length; i++) {
vertexs[i] = new Vertex(i, this.V[i]);
}
this.adj = new List[length];
for (int i = 0; i < this.N; i++) {
this.adj[i]=new ArrayList<>();
}
}
//打印邻接矩阵
public void show() {
System.out.println(" ");
for (int i = 0; i < this.N; i++) {
System.out.format("%-4c", this.V[i]);
//拿到邻接表相邻结点的集合
List<Integer> linkedList = this.adj[i];
for (int j = 0; j < linkedList.size(); j++) {
System.out.print(this.V[linkedList.get(j)] + "---->");
}
System.out.println();
System.out.format("%-4d",vertexs[i].index);
for (int j = 0; j < linkedList.size(); j++) {
System.out.print(vertexs[linkedList.get(j)].index + "---->");
}
System.out.println();
}
}
/**
* 创建顶点类
*/
private class Vertex {
char v;//值
int index;//索引
int weight;//权值
public Vertex(int index, char c) {
this.index = index;
this.v = v;
this.weight = weight;
}
public Vertex(int index) {
}
}
public static void main(String[] args) {
char arr[] = {'A', 'E', 'F', 'G', 'H', 'P'};
//构建graph01
Graph02 graph02 = new Graph02(arr);
//邻接表
List<Integer>[] adj = graph02.adj;
adj[0].add(1);
adj[0].add(2);
adj[0].add(3);
adj[1].add(0);
adj[1].add(3);
adj[1].add(4);
adj[2].add(0);
adj[3].add(0);
adj[3].add(1);
adj[3].add(4);
adj[3].add(5);
adj[4].add(1);
adj[4].add(3);
adj[4].add(5);
adj[5].add(3);
adj[5].add(4);
graph02.show();
}
}

使用邻接表求出A--P的所有路径:
package graphtheory;
import java.util.*;
// 图的表示-- 使用邻接表
public class Graph03 {
private char[] V;
// 顶点数组
private Vertex[] vertexs;
private int N;
// 邻接表
private List<Integer>[] adj;
public Graph03(char[] arr) { // {'A','E','F','G','H','P'}
int length = arr.length;
this.N = length;
this.V = Arrays.copyOf(arr, length);
// 构建图中的结点
vertexs = new Vertex[length];
for (int i = 0; i < length; i++) {
vertexs[i] = new Vertex(0, this.V[i]);
}
this.adj = new List[length];
for (int i = 0; i < this.N; i++) {
this.adj[i] = new ArrayList<>();
}
}
// 打印邻接矩阵
public void show() {
for (int i = 0; i < this.N; i++) {
System.out.format("%-4c", this.V[i]);
List<Integer> linkedList = this.adj[i];
for (int j = 0; j < linkedList.size(); j++) {
System.out.print(this.V[linkedList.get(j)] + "---->");
}
System.out.println();
System.out.format("%-4c", this.V[i]);
for (int j = 0; j < linkedList.size(); j++) {
System.out.print(linkedList.get(j) + "---->");
}
System.out.println();
}
}
public void bfs(int startIndex){
boolean visited[] = new boolean[this.N];
List<List<Integer>> result = new ArrayList<>();
// 使用队列
Queue<AbstractMap.SimpleEntry<Integer,Integer>> queue = new LinkedList<>();
// 将开始顶点入队
queue.add(new AbstractMap.SimpleEntry<>(startIndex,0));
// 设置startIndex已经被访问
visited[startIndex]=true;
while(!queue.isEmpty()){
AbstractMap.SimpleEntry<Integer,Integer> pair = queue.poll();
int key = pair.getKey(); //顶点的索引
int val = pair.getValue();// 层
if(result.size() == val){
ArrayList list = new ArrayList();
result.add(list);
}
List<Integer> levelList = result.get(val);
levelList.add(key);
// 找和key顶点直接相连的的索引
List<Integer> list = this.adj[key];
for(int i=0;i<list.size();i++){
if(!visited[list.get(i)]){
queue.add(new AbstractMap.SimpleEntry(list.get(i),val+1));
visited[list.get(i)]=true;
}
}
}
for(int i=0;i<result.size();i++){
System.out.println("level:"+(i+1));
for(int j=0;j<result.get(i).size();j++){
System.out.format("%-4d",result.get(i).get(j));
}
System.out.println();
}
}
public void dfs(int startIndex,int endIndex){
//创建一个数组,用来记录是否已经被访问
boolean visited[] = new boolean[this.N];
// 标记开始结点已经被访问过
LinkedList<Character> path = new LinkedList<>();
dfs(startIndex,endIndex,visited,path);
}
// 递归向下去找
private void dfs(int startIndex,int endIndex,boolean[] visited, LinkedList<Character> path){
// 递归终止的条件
if(startIndex == endIndex){
path.offerLast(this.V[startIndex]);
System.out.println(path);
// 从路径的尾部删掉最后的顶点
path.pollLast();
return;
}
// 将当前顶点加到路径中去
path.offer(this.V[startIndex]);
// 标识startIndex已经被访问了
visited[startIndex]=true;
// 递归操作
// 1、先找和startIndex直接连接的顶点有哪些
List<Integer> list = this.adj[startIndex];
// 2、处理每一个直接连接的顶点
for(int i=0;i<list.size();i++){
if(!visited[list.get(i)]){
dfs(list.get(i),endIndex,visited,path);
}
}
visited[startIndex]=false; // 回溯
path.pollLast();
}
private class Vertex {
char v;
int index;
//权值
int weight;
public Vertex(int index, char v, int weight) {
this.index = index;
this.v = v;
this.weight = weight;
}
public Vertex(int index, char v) {
this(index, v, 1);
}
}
public static void main(String[] args) {
char arr[] = {'A', 'E', 'F', 'G', 'H', 'P' };
Graph03 graph03 = new Graph03(arr);
// 邻接表
List<Integer>[] adj = graph03.adj;
adj[0].add(1);
adj[0].add(2);
adj[0].add(3);
adj[1].add(0);
adj[1].add(3);
adj[1].add(4);
adj[2].add(0);
adj[3].add(0);
adj[3].add(1);
adj[3].add(4);
adj[3].add(5);
adj[4].add(1);
adj[4].add(3);
adj[4].add(5);
adj[5].add(3);
adj[5].add(4);
graph03.bfs(5);
}
}
迪杰斯特拉算法
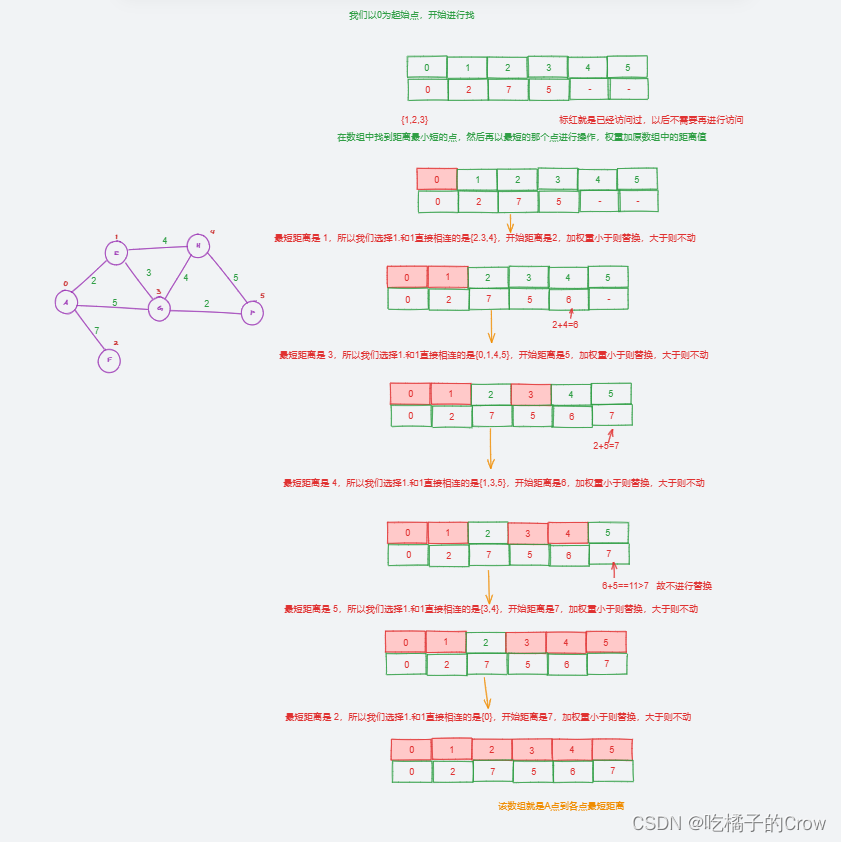
概念:即先求出长度最短的一条最短路径,再参照它求出长度次短的一条最短路径,依次类推,直到从源点v 到其它各顶点的最短路径全部求出为止。

假设我们求A点到各点的最短距离
package graphtheory;
import java.util.*;
// 图的单源最最短路径-迪杰斯特拉算法(从一个顶点到图中各个顶点的最短距离)
public class Graph04 {
private char[] V;
// 顶点数组
private Vertex[] vertexs;
private int N;
// 邻接表
private List<AbstractMap.SimpleEntry<Integer, Integer>>[] adj; // key:顶点索引,val:权值
public Graph04(char[] arr) { // {'A','E','F','G','H','P'}
int length = arr.length;
this.N = length;
this.V = Arrays.copyOf(arr, length);
// 构建图中的结点
vertexs = new Vertex[length];
for (int i = 0; i < length; i++) {
vertexs[i] = new Vertex(i, this.V[i]);
}
this.adj = new List[length];
for (int i = 0; i < this.N; i++) {
this.adj[i] = new ArrayList<>();
}
}
public int[] dijkstra(int sourceIndex) {
// 1、创建距离表
int[] dist = new int[this.N];
Arrays.fill(dist, Integer.MAX_VALUE);
// 2、创建一个标识顶点是否被访问的数组
boolean[] visited = new boolean[this.N];
// 3、初始化距离表
// 3-1
dist[sourceIndex] = 0; // 自身到自身的距离
visited[sourceIndex] = true;
// 3-2、找和sourceIndex直接相连的顶点
List<AbstractMap.SimpleEntry<Integer, Integer>> list = this.adj[sourceIndex];
for (int i = 0; i < list.size(); i++) {
AbstractMap.SimpleEntry<Integer, Integer> vertex = list.get(i);
int key = vertex.getKey();//顶点索引
int val = vertex.getValue();//权值
// 3-3 更新距离表
dist[key] = val;
}
for (int k = 1; k < this.N; k++) {
//4、在上述的最短路径dist[]中,从未被访问的顶点中选一条最短的路径长度
int minDist = Integer.MAX_VALUE;
int minDistIndex = -1;
for (int i = 0; i < this.N; i++) {
if (!visited[i] && dist[i] != Integer.MAX_VALUE && dist[i] < minDist) {
minDist = dist[i];
minDistIndex = i;
}
}
// 最最短的路径长度所在的顶点与其它顶点都没有相连
if (minDistIndex == -1) {
break;
}
//5、更新距离表()
// 5-1 将最最短的路径长度所在的顶点设置成已访问
visited[minDistIndex] = true;
// 5-2 找到和最短路径长度所在顶点直接相连的顶点
List<AbstractMap.SimpleEntry<Integer, Integer>> list2 = this.adj[minDistIndex];
// 5-3 minDist+权值与距离表中的数据进行比较
for (int i = 0; i < list2.size(); i++) {
AbstractMap.SimpleEntry<Integer, Integer> vertex = list2.get(i);
int key = vertex.getKey();//顶点索引
int val = vertex.getValue();//权值
int newVal = minDist + val;
if (!visited[key] && newVal < dist[key]) {
dist[key] = newVal;
}
}
}
return dist;
}
private class Vertex {
char v;
int index;
public Vertex(int index, char v) {
this.index = index;
this.v = v;
}
}
public static void main(String[] args) {
char arr[] = {'A', 'E', 'F', 'G', 'H', 'P'};
Graph04 graph04 = new Graph04(arr);
// 邻接表
List<AbstractMap.SimpleEntry<Integer, Integer>>[] adj = graph04.adj;
adj[0].add(new AbstractMap.SimpleEntry<>(1, 5));
adj[0].add(new AbstractMap.SimpleEntry<>(2, 4));
adj[0].add(new AbstractMap.SimpleEntry<>(5, 2));
adj[1].add(new AbstractMap.SimpleEntry<>(0, 5));
adj[1].add(new AbstractMap.SimpleEntry<>(5, 1));
adj[1].add(new AbstractMap.SimpleEntry<>(4, 3));
adj[2].add(new AbstractMap.SimpleEntry<>(0, 4));
adj[3].add(new AbstractMap.SimpleEntry<>(4, 3));
adj[3].add(new AbstractMap.SimpleEntry<>(5, 4));
adj[4].add(new AbstractMap.SimpleEntry<>(1, 3));
adj[4].add(new AbstractMap.SimpleEntry<>(5, 2));
adj[4].add(new AbstractMap.SimpleEntry<>(3, 3));
adj[5].add(new AbstractMap.SimpleEntry<>(0, 2));
adj[5].add(new AbstractMap.SimpleEntry<>(1, 1));
adj[5].add(new AbstractMap.SimpleEntry<>(4, 2));
adj[5].add(new AbstractMap.SimpleEntry<>(3, 4));
int[] dist = graph04.dijkstra(0);
System.out.println(Arrays.toString(dist));
}
}








![OKHttp_官方文档[译文]](https://img-blog.csdnimg.cn/20200422165028899.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0ZEb3VibGVtYW4=,size_16,color_FFFFFF,t_70#pic_center)