上一篇写到了一致性模型，而因果一致性模型比较复杂，故单独写一篇文章来记录

强一致性模型会在网络分区时变的不可用，而最终一致性模型放弃了safety，但同时也对系统可用性和性能产生明显的损害。上层要做些操作。于是有了一个折中

 

因果一致性单独条件

因果一致性遵守下面三条规则：

1. 单进程写操作有序。

2. “writes follow reads”规则。

3. 因果关系可传递。

writes follow reads”指的是，假设第一个进程先读取到了数据对象x=5，后写入了另一个数据对象y=10，然后第二个进程读到了y=10，那么接下来如果这个进程读取数据对象x的值，那么不能读到一个比x=5更旧的值

跟线性一致性和顺序一致性的定义一样，因果一致性也是表达了系统对于读写操作的某种排序规则。为此我们首先需要定义清楚一个关键概念——因果顺序 (causality order)，它表明了两个不同操作之间的排序是怎样规定的。

因果顺序是一种偏序关系

定义

 

你可能会产生疑问，那么这顺序一致性也是这样啊？

也就是说，因果关系是站在一进程看问题， 而顺序一致性是站在全局一致性

所以下面就有个例子

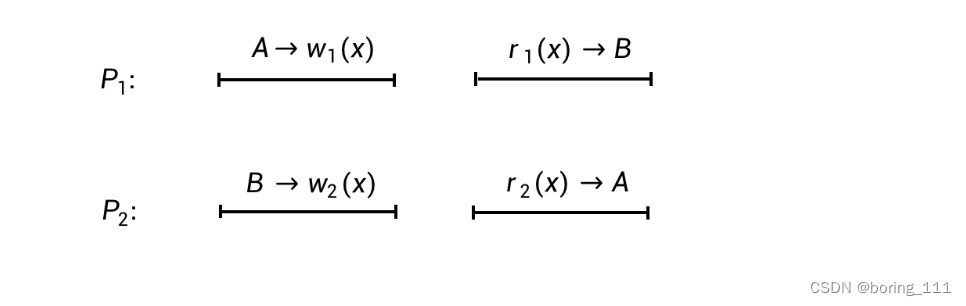
站在P1视角，有：

1. A --> w1(x)

2. B --> w2(x)

3. r1(x) --> B

站在P2视角，有：

1. B --> w2(x)

2. A --> w1(x)

3. r2(x) --> A

不同参照系的观察者对于不同事件的先后顺序，可能产生不同的看法。实际上，分别站在进程P1和P2的视角上，它们看到的都没有什么矛盾。矛盾发生在我们站在全局视角去看的时候。

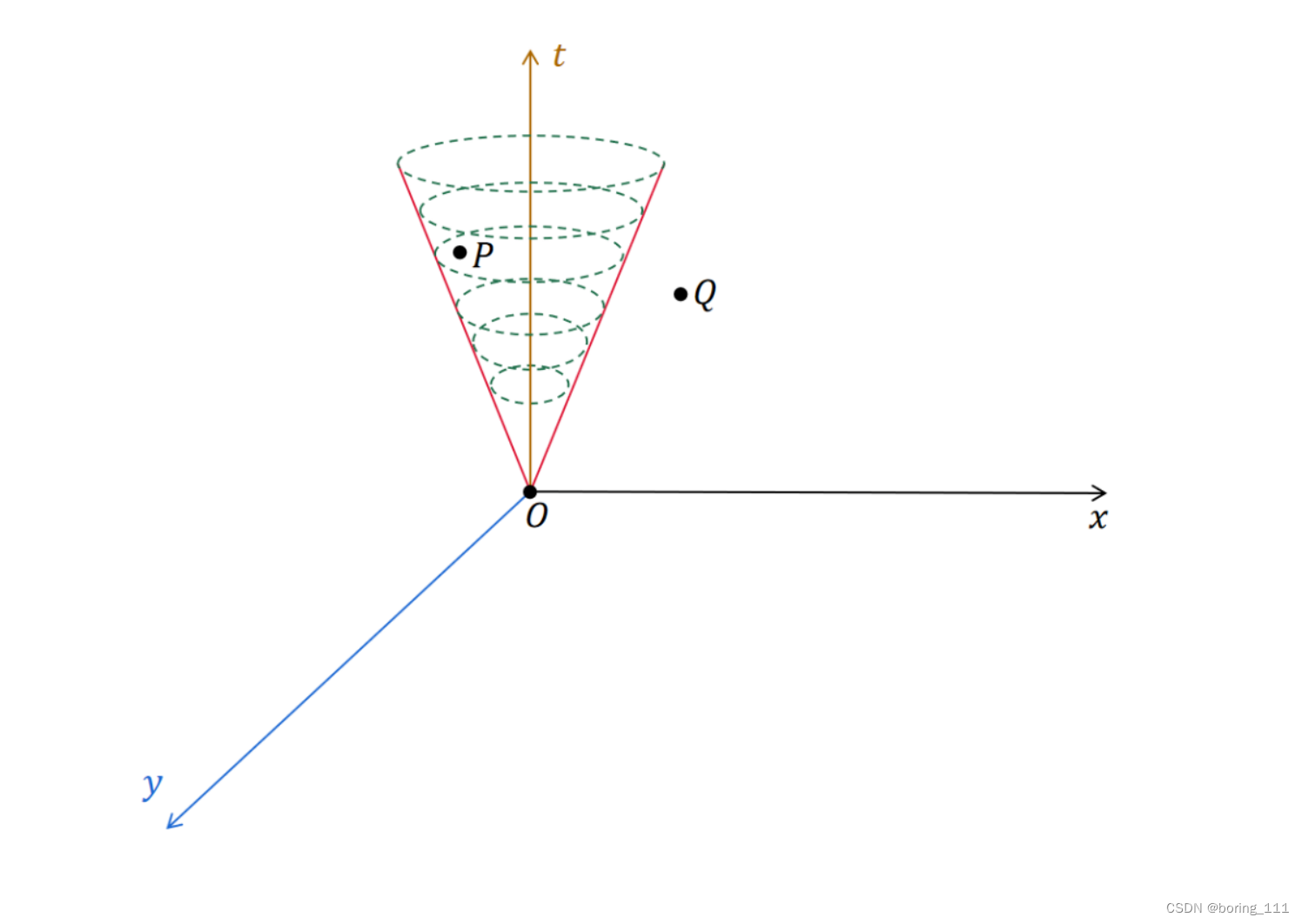
其实就只要满足在Lamport时钟中提到的happen-before关系即可

也就是在这个时间光锥里面，我们满足偏序关系，而站在别的地方，我们可能看到不同的发生序列

比如 三体星系上发生了某个重大事件，按照绝对时空观的观点，它也可能对现在的你产生了影响。你大概会同意，这是不可能的，因为三体星系即使以最快的速度向地球传递信息，也要在4年之后才能到达。

 

 

Reference

条分缕析分布式：因果一致性和相对论时空