2021年国赛高教杯数学建模

A题 FAST主动反射面的形状调节

原题再现

  中国天眼——500 米口径球面射电望远镜（Five-hundred-meter Aperture Spherical radio Telescope，简称 FAST），是我国具有自主知识产权的目前世界上单口径最大、灵敏度最高的射电望远镜。它的落成启用，对我国在科学前沿实现重大原创突破、加快创新驱动发展具有重要意义。
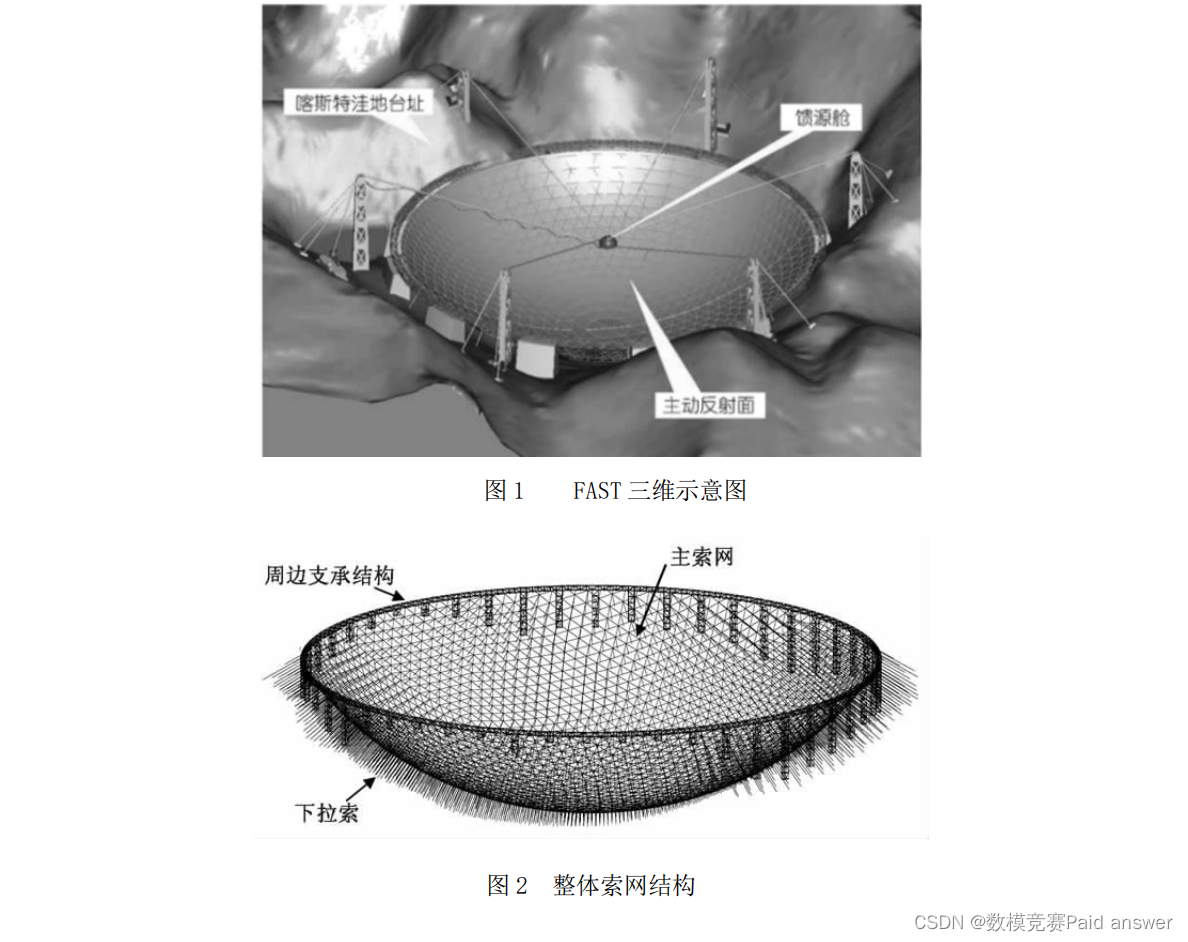
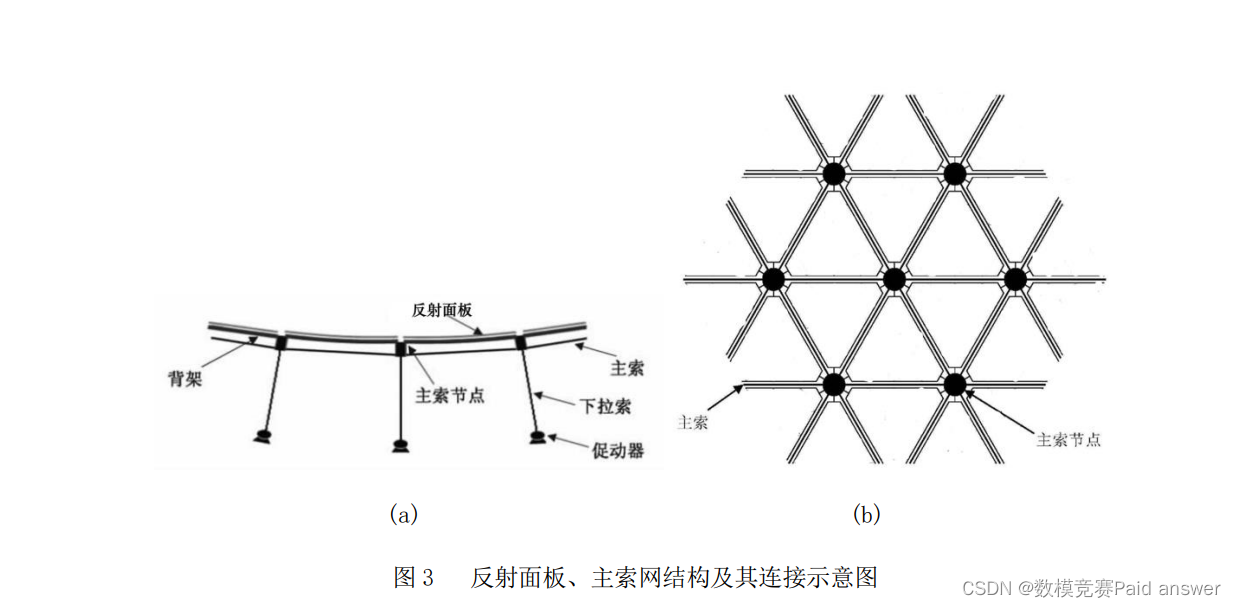
  FAST 由主动反射面、信号接收系统（馈源舱）以及相关的控制、测量和支承系统组成（如图 1 所示），其中主动反射面系统是由主索网、反射面板、下拉索、促动器及支承结构等主要部件构成的一个可调节球面。主索网由柔性主索按照短程线三角网格方式构成，用于支承反射面板（含背架结构），每个三角网格上安装一块反射面板，整个索网固定在周边支承结构上。每个主索节点连接一根下拉索，下拉索下端与固定在地表的促动器连接，实现对主索网的形态控制。反射面板间有一定缝隙，能够确保反射面板在变位时不会被挤压、拉扯而变形。索网整体结构、反射面板及其连接示意图见图2和图3。


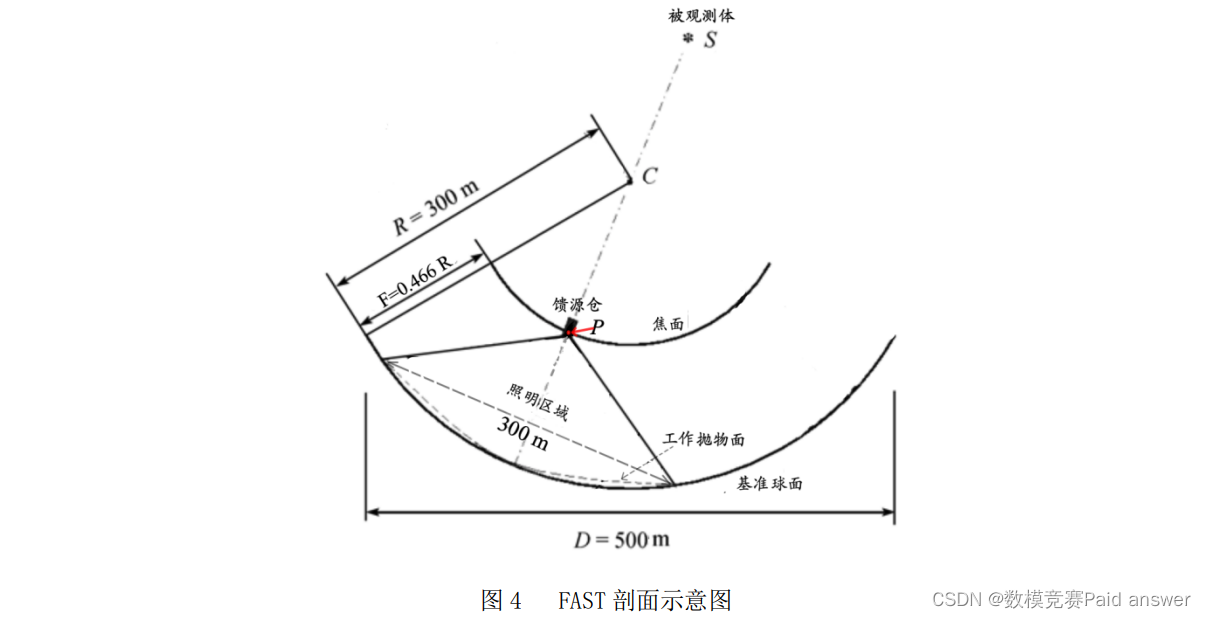
  主动反射面可分为两个状态：基准态和工作态。基准态时反射面为半径约 300 米、口径为500 米的球面（基准球面）；工作态时反射面的形状被调节为一个 300 米口径的近似旋转抛物面（工作抛物面）。图 4 是 FAST 在观测时的剖面示意图，C 点是基准球面的球心，馈源舱接收平面的中心只能在与基准球面同心的一个球面（焦面）上移动，两同心球面的半径差为 F=0.466R（其中 R 为基准球面半径，称 F/R 为焦径比）。馈源舱接收信号的有效区域为直径 1 米的中心圆盘。当 FAST 观测某个方向的天体目标 S 时，馈源舱接收平面的中心被移动到直线 SC 与焦面的交点 P 处，调节基准球面上的部分反射面板形成以直线 SC 为对称轴、以 P 为焦点的近似旋转抛物面，从而将来自目标天体的平行电磁波反射汇聚到馈源舱的有效区域。

  将反射面调节为工作抛物面是主动反射面技术的关键，该过程通过下拉索与促动器配合来完成。下拉索长度固定。促动器沿基准球面径向安装，其底端固定在地面，顶端可沿基准球面径向伸缩来完成下拉索的调节，从而调节反射面板的位置，最终形成工作抛物面。
  本赛题要解决的问题是：在反射面板调节约束下，确定一个理想抛物面，然后通过调节促动器的径向伸缩量，将反射面调节为工作抛物面，使得该工作抛物面尽量贴近理想抛物面，以获得天体电磁波经反射面反射后的最佳接收效果。
  请你们团队根据附录中的要求及相关参数建立模型解决以下问题：
  1、当待观测天体𝑆位于基准球面正上方，即𝛼 = 0°, 𝛽 = 90°时，结合考虑反射面板调节因素，确定理想抛物面。
  2、当待观测天体𝑆位于𝛼 = 36.795°, 𝛽 = 78.169°时，确定理想抛物面。建立反射面板调节模型，调节相关促动器的伸缩量，使反射面尽量贴近该理想抛物面。将理想抛物面的顶点坐标，以及调节后反射面 300 米口径内的主索节点编号、位置坐标、各促动器的伸缩量等结果按照规定的格式（见附件 4）保存在“result.xlsx”文件中。
  3、基于第 2 问的反射面调节方案，计算调节后馈源舱的接收比，即馈源舱有效区域接收到的反射信号与 300 米口径内反射面的反射信号之比，并与基准反射球面的接收比作比较。

整体求解过程概述(摘要)

  本文针对“FAST”主动反射面形状调节的应用问题，基于合适的量化指标，建立理想抛物面分布模型、反射面板调节模型和馈源舱、基准球面接收比计算模型。通过三维坐标变换、空间对称性进行模型简化，采用变步长搜索法、粒子群优化算法等求解模型。最终根据模型的结果得到了对于不同情况下“FAST”获得最佳电磁波接收效果的主动反射面形状调节策略。
  针对问题一，首先建立含有变量 p（焦距二倍）的抛物面方程。由于促动器的工作行程可用抛物面与基准球面之间间隙的体积表示，故进行体积积分得到间隙体积表达式，从而建立以p为自变量、以间隙体积最小为目标、以促动器径向伸缩范围为限制条件的单目标优化模型。利用变步长搜索法求解模型，得到当 p=280.38m时，达到最小间隙体积，即得理想抛物面方程x’2+y’2=2×280.38·(z+160.2+140.19)。
  针对问题二，先进行三维坐标变换，将一般的坐标变换为问题一的特殊情形，再运用问题一的理想抛物面分布模型求解观测一般位置天体S时的理想抛物面方程，得理想抛物面顶点坐标为(-49.376795,-36.931929,-294.36086)。然后基于粒子群优化算法，建立以相关促动器伸缩量△L为自变量、以相关反射面板重心和对应节点到理想抛物面的距离最小为目标的双目标优化模型。施加权重将多目标优化问题化为单目标优化问题。利用变步长搜索法求解模型，得到调节后300m口径内的主索节点编号、位置坐标、各促动器的伸缩量（见正文模型Ⅱ的求解结果中附件4截图、图7）。
  针对问题三，馈源舱的接收比可用主动反射面有效反射面积在xOy面上的投影与300m口径的面积之比来表示。由几何关系可求得任意一块反射面板的有效反射面积。最终求解得到的馈源舱的接收比为1.43%。通过球形凹面反射镜的光学与几何性质推导出接收范围的面积大小，列出入射光线位置与接收范围的关系，从而求出基准反射球面的接收比为1.11×〖10〗^(-5)，最后进行比较。
  为使模型更加合理，本文最后对模型Ⅱ、Ⅲ进行了误差分析，针对模型Ⅲ的有关参数进行了灵敏度分析。通过误差分析发现该模型误差较小并且收敛，故所建立的模型及其结果具有一定的可靠性。通过灵敏度分析发现，馈源舱的直径对馈源舱的接收比影响较大，且灵敏度在该范围内保持不变；而促动器径向伸缩范围则对馈源舱的接收比显示很强的稳定性。故可以通过增加馈源舱直径的方式来增大接收比。

模型假设：

  为了适当地简化模型，本文做出如下假设：
  1. 设抛物面的反射率为 1，且符合镜面反射；
  2. 待观测天体 S 与“FAST”的相对位置保持不变；
  3. 反射面板上的漏水小孔对电磁波的反射无影响，故可认为反射面板无孔；
  4. 目标天体发射的电磁波为平行电磁波且沿直线传播；
  5. 假定“FAST”最低端主索节点对应的促动器也可以径向伸缩；
  6. 馈源舱对电磁波无遮挡；
  7. 构成反射面的三角板视为平面板。

问题分析：

  本题的研究对象是“FAST”主动反射面的形状，目的是根据促动器的径向伸缩范围、理想抛物面的口径大小，在不同的天体方位情况下，确定理想抛物面的方程，通过改变相关促动器的径向伸缩量△L，在已知理想抛物面的情况下，使实际抛物面尽量接近理想抛物面，以获得天体电磁波信号的最佳接收效果。
  问题一是建立理想抛物面的分布模型，问题二是建立反射面板的调节模型，问题三是建立馈源舱、基准球面接收比的计算模型。因此解决问题一是基础。
   问题一：研究当待测天体 S 位于基准球面正上方时理想抛物面的确定
  问题一题目给出了一种最简单的观测情况，本质上是在促动器的径向伸缩范围内计算基准球面变换成理想抛物面的操作复杂度，即促动器的工作行程。建立一种抛物面筛选的判据，寻找一个变换操作复杂度最小的抛物面，确定其方程。
  具体步骤如下：
  (1) 确定促动器的径向伸缩范围；
  (2) 分析以球心为原点的直角坐标系下的符合条件的待筛选抛物面，建立待筛选抛物面的直角坐标方程；
  (3) 确定待筛选抛物面与基准球面之间的间隙体积；
  (4) 比较各个间隙体积的大小，确定理想抛物面方程。
   问题二：研究一般情况下理想抛物面的确定及反射面板的调节策略
  问题二需在问题一模型的基础上进行改进以适应天体在一般位置的情况下理想抛物面方程的确定。在理想抛物面已知的情况下，通过建立一种反射面与理想抛物面贴近程度的量化指标，来筛选最佳反射面板的调节策略。并记录此时的相关信息。
  附件 1 给出了所有主索节点的坐标和编号信息，附件 2 给出了促动器下端点坐标、基准态时上端点的坐标和对应主索节点的编号，附件 3 给出了每块反射面板对应主索节点的编号。根据题给附件和最佳反射面的直角坐标方程，可以确定调节后反射面相关主索节点的编号、位置坐标、各促动器的伸缩量等结果。
   问题三：研究馈源舱的接收比并与基准反射球面的接收比作比较
  馈源舱的接收比可等效为主动反射面有效反射面积在 xOy 面上的投影与300m 口径面积的比值。主动反射面有效反射面积在 xOy 面上的投影可以通过几何关系求出。
  通过球形凹面反射镜的光学与几何性质推导出入射光线位置与接收范围的关系，接受范围的面积与 300m 口径的面积之比即为基准反射球面的接收比。比较两接收比，得出结论。

模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：(代码和文档not free)

P=[X,Y,Z];
theta1=-36.795/180*pi;%绕z轴旋转的角度
theta2=-11.831/180*pi;%绕y轴旋转的角度
Q1=[cos(theta1),sin(theta1),0
-sin(theta1),cos(theta1),0
0 0 1];%坐标变换矩阵1
Q2=[cos(theta2) 0 -sin(theta2) 
0 1 0  
sin(theta2) 0 cos(theta2) ];%坐标变换矩阵2
P1=zeros(2226,3);
for i=1:2226
    P1(i,:)=P(i,:)*Q1*Q2;
end
angle=zeros(2226,1);
angle1=zeros(2226,1);
for i=1:2226
    angle(i)=acos(-P1(i,3)/norm(P1(i,:)));%计算与z轴的夹角
    angle1(i)=atan(P1(i,1)/P1(i,2));
end
p=280.38;
re=zeros(2226,1);
re1=zeros(2226,1);
%求得每支促动器的伸缩范围
for i=1:2226
    xx=-p*cot(angle(i))+sqrt(p^2*cot(angle(i)).^2+320.4*p+p^2);
    yy=-cot(angle(i))*xx;
    re(i)=(sqrt(xx^2+yy^2)-300);
    re1(i)=re(i)/norm(P1(i,:));%记录倍数
end
a=find(abs(re)<0.6);%找到符合条件的点
%a=find((P1(a,1).^2+P1(a,2).^2)<22500);%进一步筛选
k=1;
for i=1:length(a)
    if (P1(a(i),1)^2+P1(a(i),2)^2)<22500
        b(k)=a(i);
        k=k+1;
    end
end
P2=zeros(length(b),1);
P2=P(b,:).*(1+re1(b));
Name=str(b);%找出相应的编号,str为编号的数据

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可