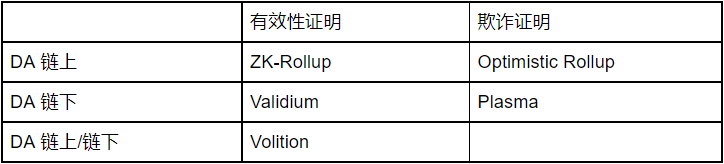
电容是指容纳电荷的能力,在给定电位差下自由电荷的储藏量,记为C,国际单位是法拉(F)。
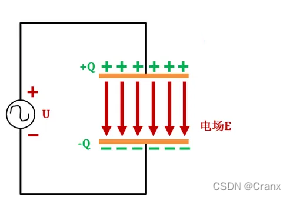
如上图所示,以平行板电容器为例,简单介绍下电容的基本原理。
在两块距离较近、相互平行的金属平板上(平板之间为电介质)加载一个直流电压;稳定后,与电压正极相连的金属平板将呈现一定量的正电荷,而与电压负极相连的金属平板将呈现相等量的负电荷;这样,两个金属平板之间就会形成一个静电场,所以电容是以电场能的形式储存电能量,储存的电荷量为Q。
电容储存的电荷量Q与电压U和自身属性(也就是电容值C)有关,也就是Q=U*C。根据理论推导,平行板电容器的电容公式如下:

理想电容内部是介质,没有自由电荷,不可能产生电荷移动也就是电流,那么理想电容是如何通交流隔直流呢?
从理论上来讲,电荷是根本不能在电容中流动的。因为在平行板电容上电后,一块板带正电,另一块板带负电,在两快板之间的非导电介质不能使两种电荷相互转移并接触,完成电荷流动。真能通过,那也代表着电容被击穿了,无法使用了。
所以直流是肯定不能通过电容的,但为什么交流反而可以呢?
事实上,当电容接通电源时,实际上自由电荷没有通过两极间的绝缘介质,直流是如此,交流亦是如此。
但是,交流电的电压是不断变化的,积累在两极板上的电荷发生变化,引起两极板间的电压变化,当电压升高时,电荷向电容的极板上聚集,形成充电电流;当电压降低时,电荷离开极板,形成放电电流。不断地充电和放电,对外电路来说就有了电流,这也就是电容通交流的原因,即便电荷没有真的通过极板。
- 通交流隔直流需注意的两点
- 电容接上直流电,也会产生电流
当电容两端接通直流电源时,会进入充电状态,电路中产生充电电流,不过这个时间太短太短,一般只需要千分之一秒左右瞬间完成充电。当电容器的电场力与电源力平衡时,电荷就不再移动,充电过程结束,电路中就不再有电流通过,所以就表现出来直流电无法通过电容的现象。

-
- 不是所有交流电都能通过电容
当电容两端接上交流电源时,因交流电的大小与方向不断交替变化,就使电容不断进行充电与放电,电路始终有电流流通,所以说电容可通交流。
但这里有个问题,就是如果电容很快充完电了,但交流电还没有变化(从正半周变化到负半周),那此时就类似直流电的情况,即电路没电流了,相当于断路。直到等到交流电负半周到来,电容放电,电路才重新产生电流。这意味着,如果交流电频率较低(变化速度慢),接上电容时会中途断电流,即电路不是完全导通。如果频率超级低,无限接近于0,那电路就会看起来不通。
所以不是所有交流电都能通过电容,而是高频率导通,低频率阻断。