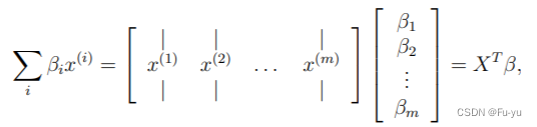前言
参考用书:王道考研《2024年 数据结构考研复习指导》
参考用书配套视频:4.1_1_串的定义和基本操作_哔哩哔哩_bilibili
特别感谢: Google Bard老师[解释KMP,修改BUG]、Chat GPT老师[修改BUG]、BING老师[封面图]~

当我请求BING老师:画一张串的图片,于是BING老师画了一幅:“串的图片”;意外地很好看有没有....😶
考研笔记整理,内容包含串的基本定义,暴力匹配、KMP模式匹配C++代码~考研一起加油~ 🐑
第1版:查资料、画导图、配图、写BUG~~
第2版:发现自己在next设置的表格总是被吞...补上原来的表,更改朴素匹配算法、KMP优化算法的描述;更换封面,修改标题~~
目录
前言
目录
思维导图
串的定义和实现
串的定义
串的存储结构
串的基本操作
定长顺序存储(代码)
堆分配顺序存储(代码)
串的模式匹配
朴素/暴力匹配算法
算法思想
核心代码
举栗实现
KMP算法
算法思想
核心代码
举栗实现
KMP优化算法
算法思想
核心代码
求next数组与nextval数组
推算思路
结语
思维导图
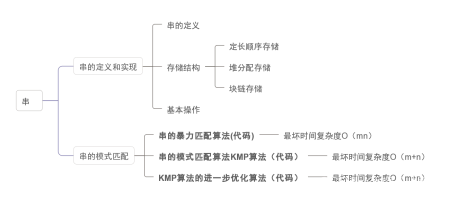
思维导图备注
- 考研大纲仅要求掌握字符串模式匹配,重点在KMP匹配算法,以及匹配算法中Next数组的手动推算[贴在了最后一部分]~
- 考研大纲对于串的定义和实现没有要求,但是为了保证博文的完整性还是写完这部分了,考研小伙伴们随便看看就行~
串的定义和实现
串的定义
串的定义: 由零个或多个字符组成的有限序列。一般记为
![]()
其中,a1可以是字母、数字或者其它字符。
串的逻辑结构:和线性表极为相似,区别仅在与串的数据对象为字符集。在基本操作上,串和线性表有很大区别。线性表的基本操作主要以单个元素作为操作未向,如查找、插入或删除某个元素等;而串的基本操作通常以子串作为操作对象,如查找、插入或删除一个子串等。
串的存储结构
串的定长顺序存储:类似于线性表的顺序存储结构,用一组地址连续的存储单元存储串值的字符序列。在串的定长顺序存储结构中,(1)为每个串变量分配一个固定长度的存储区,或(2)串的长度加上空终止符。
串的堆分配存储:堆分配存储表示依然以一组地址连续的存储单元存放串值的字符序列,但他们的存储空间是在程序执行过程中动态分配得到的。
串的块链存储:类似于线性表的链式存储结构,也可以采用链式表存储串值。由于串的特殊性(每个元素只有1个字符),在具体实现时,每个结点既可以存放一个字符,也可以存放多个字符。每个结点称为块,整个链表称为块链结构。
三种串的存储结构如下图所示:
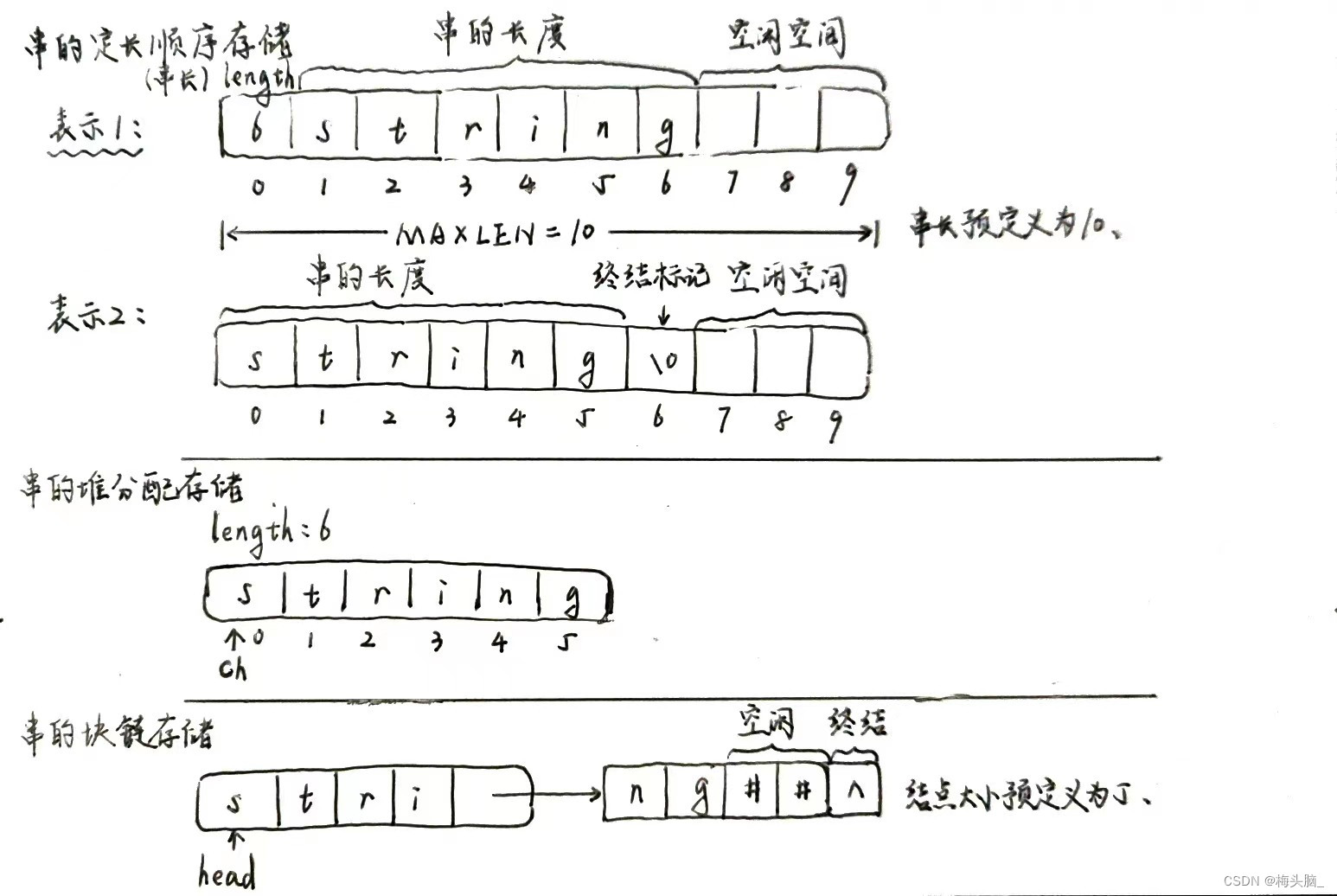
图:串的定长顺序存储、堆分配存储、块链存储示意图
三种存储方式优缺点比较:
| 存储方式 | 优点 | 缺点 |
|---|---|---|
| 定长顺序存储 | (1)易于实现和管理 (2)为高级设计程序所采用 | 字符串必须是固定长度的。如果字符串比分配的空间短,会浪费空间;如果字符串比分配的空间长,会截断字符串。 |
| 堆分配存储 | (1)字符串可以是任意长度 (2)为高级设计程序所采用 | 实施和管理比定长顺序存储更复杂。 |
| 块链存储 | (1)字符串可以是任意长度 (2)适合字符串被频繁修改的场合 | 实现和管理比定长顺序存储或堆分配存储更复杂。 |
串的基本操作
块链存储目前不是很常用,在此暂时不作讨论~🫥
- 第一份代码,不使用C++内置函数实现代码功能,采用定长顺序存储~
- 第二份代码,使用C++内置函数实现代码功能,此功能默认为动态分配~
定长顺序存储(代码)
#include <iostream>
#include <string>
#define MAXLEN 25
//定长顺序存储表示存储结构:内容与长度
typedef struct{
char ch[MAXLEN];
int length;
}SString;
//初始化
void initString(SString *s) {
s->length = 0;
s->ch[0] = '\0';
}
//输出字符串的内容及长度
void printString(const SString *s) {
std::cout << s->length << ": ";
for (int i = 1; i <= s->length; i++) {
std::cout << s->ch[i];
}
std::cout << std::endl;
}
//读取字符串
void readString(SString *s) {
std::string str;
std::getline(std::cin, str);
for (int i = 0; i < str.length(); i++) {
s->ch[++s->length] = str[i];
}
}
//比较字符串
int compareString(const SString *s1, const SString *s2) {
if (s1->length != s2->length) {
return s1->length - s2->length;
}
for (int i = 0; i < s1->length; i++) {
if (s1->ch[i] != s2->ch[i]) {
return s1->ch[i] - s2->ch[i];
}
}
return 0;
}
//连接字符串
void concatString(SString *s1, const SString *s2) {
if (s1 == nullptr || s2 == nullptr) {
return;
}
if (s1->length + s2->length > MAXLEN - 1) {
std::cout << "String is too long.\n";
return;
}
for (int i = 1; i <= s2->length; i++) {
s1->ch[s1->length + i] = s2->ch[i];
}
s1->length += s2->length;
}
//获取字符串索引
int indexOfChar(const SString *s, char c) {
for (int i = 0; i < s->length; i++) {
if (s->ch[i] == c) {
return i;
}
}
return -1;
}
//清空字符串
void clearString(SString *s) {
s->length = 0;
s->ch[0] = '\0';
}
//销毁字符串
void destroyString(SString *s) {
initString(s);
}
int main() {
SString s1, s2;
initString(&s1);
initString(&s2);
std::cout << "输入字符串1: ";
readString(&s1);
std::cout << "输入字符串2: ";
readString(&s2);
std::cout << std::endl;
std::cout << "输出字符串1: ";
printString(&s1);
std::cout << "输出字符串2: ";
printString(&s2);
std::cout << std::endl;
std::cout << "比较字符串: " << compareString(&s1, &s2) << std::endl;
std::cout << std::endl;
concatString(&s1, &s2);
std::cout << "输出字符串2并入字符串1的内容: ";
printString(&s1);
std::cout << std::endl;
std::cout << "查询字符 'a'在字符串1的位置: " << indexOfChar(&s1, 'a') << std::endl;
std::cout << std::endl;
clearString(&s1);
std::cout << "输出执行清空后字符串1的内容: ";
printString(&s1);
std::cout << std::endl;
destroyString(&s1);
return 0;
}
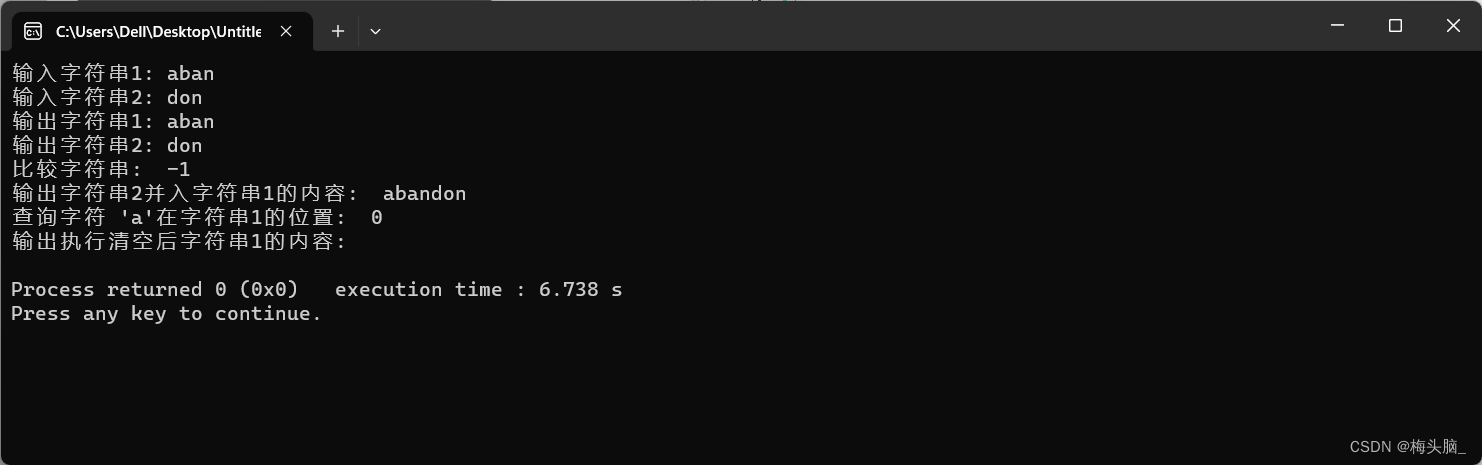
执行结果如下图所示:

堆分配顺序存储(代码)
#include <iostream>
#include <string>
#include <cstring>
#include <algorithm>
int main() {
std::string s1, s2;
std::cout << "输入字符串1: ";
std::getline(std::cin, s1);
std::cout << "输入字符串2: ";
std::getline(std::cin, s2);
std::cout << "输出字符串1: " << s1 << std::endl;
std::cout << "输出字符串2: " << s2 << std::endl;
std::cout << "比较字符串: " << std::strcmp(s1.c_str(), s2.c_str()) << std::endl;
s1 = s1 + s2;
std::cout << "输出字符串2并入字符串1的内容: " << s1 << std::endl;
std::cout << "查询字符 'a'在字符串1的位置: " << std::find(s1.begin(), s1.end(), 'a') - s1.begin() << std::endl;
s1.clear();
std::cout << "输出执行清空后字符串1的内容: " << s1 << std::endl;
//std::delete[] s1.c_str(); // 清空字符串这行实际不需要
return 0;
}执行结果如下图所示:
串的模式匹配
字符串匹配算法:字符串匹配算法是一种计算机算法,可在另一个字符串(也称为搜索字符串或文本)中查找一个或多个字符串(也称为模式)的位置。
模式匹配定义:子串的定位操作通常称为串的模式匹配,它求的是子串(常称“模式串”)在主串中的位置。
朴素/暴力匹配算法
算法思想
朴素的字符串匹配算法是一种用于查找文本中模式首次出现的简单算法。 它的工作原理是将模式的字符与文本的字符一个一个地进行比较,直到找到模式或到达文本的末尾。
该算法的工作原理如下:
- 初始化两个指针,i 和 j。i指向主串中的当前字符,j指向模式串中的当前字符,从前向后依次比较;
- 比较 i 和 j 处的字符:1)若相等,则将两个指针向后移动一个位置(i++,j++),并重复本步骤。2)若不等,i回溯到主串匹配字符串中首位的下1位(2+i-j),j回溯到子串的第1位(j=1);
- 如果 j 指针匹配到末尾,表示找到了匹配的串,返回主指针的位置(i-T.length);
- 如果 i 指针匹配到末尾,表示未找到匹配的串,返回-1。

图:串的朴素匹配算法举栗(共5趟)
核心代码
int index(const SString& S, const SString& T) {
int i = 1, j = 1;
while (i <= S.length && j <= T.length) {
if (S.ch[i] == T.ch[j]) { // 如果主串与子串相等
i++; // 继续比较后续字符
j++;
} else { // 如果主串与子串不相等
i = i - j + 2; // 主串指针移动到下一位
j = 1; // 子串回溯到位置1开始匹配
}
}
if (j > T.length) // 如果子串匹配到末尾相等
return i - T.length; // 返回匹配成功的主串位序
else // 如果主串匹配到末尾没有相等
return -1; // 返回-1,表示未找到匹配
}
举栗实现
#include <iostream>
#include <string>
#define MAXLEN 25
struct SString {
char ch[MAXLEN];
int length;
};
void initString(SString& s) {
s.length = 0;
s.ch[0] = '\0';
}
void readString(SString& s) {
std::string str;
std::getline(std::cin, str);
for (int i = 0; i < str.length(); i++) {
s.ch[i + 1] = str[i];
s.length++;
}
}
int index(const SString& S, const SString& T) {
int i = 1, j = 1;
while (i <= S.length && j <= T.length) {
if (S.ch[i] == T.ch[j]) {
i++;
j++;
} else {
i = i - j + 2;
j = 1;
}
}
if (j > T.length)
return i - T.length;
else
return -1;
}
int main() {
SString s1, s2;
initString(s1);
initString(s2);
std::cout << "输入主串: ";
readString(s1);
std::cout << "输入子串: ";
readString(s2);
int pos = index(s1, s2);
if (pos != -1) {
std::cout << "子串在主串中的位置: " << pos << std::endl;
} else {
std::cout << "未找到匹配位置" << std::endl;
}
return 0;
}
上述程序执行结果如下~

朴素的字符串匹配算法易于实现和理解。 但是,由于他的工作原理是比较主串和子串的每1个字符,因此朴素字符串匹配算法的最坏情况时间复杂度为 O(m*n),其中 m 是模式的长度,n 是文本的长度~
KMP算法
算法思想
Knuth-Morris-Pratt 算法是一种字符串搜索算法,通常用于查找文本中的模式。 该算法首先创建一个模式前缀表 [前缀表推算可见本文:求next数组与nextval数组] 。 然后使用该表快速跳过与模式不匹配的文本部分。
该算法的工作原理如下:
- 初始化两个指针,`i` 和 `j`。 `i` 指向文本中的当前位置,`j` 指向模式串中的当前位置。
- 比较`i` 和 `j` 处的字符。 如果它们相等,则将两个指针向后移动。
- 如果字符不相等,则将`i`向前移动匹配“i”处字符的模式的最长前缀的长度,`j`回溯到next[]指向的字符。
- 重复步骤 2 和 3,直到 `i` 到达文本末尾或 `j` 到达模式末尾。
- 如果 j 到达模式的末尾,则该模式已在文本中找到。 该算法返回模式的第一个字符在文本中的位置。
- 如果 `i` 在 `j` 到达模式末尾之前到达文本末尾,则该模式尚未在文本中找到。 该算法返回 -1。
KMP 算法是一种在文本中查找模式的非常有效的算法。 它通常用于文本编辑器、搜索引擎和其他需要在大量文本中查找模式的应用程序。

图:串的KMP匹配算法举栗(共4趟)
核心代码
//求子串的next值,快速跳过与模式不匹配的文本部分
void get_next(const SString& T, int next[]){
int i=1,j=0; //i为子串位序,j为对应的next[]值
next[1]=0; //若从主串第1位匹配失败,则下次子串从j=0位开始匹配
while(i<T.length){ //当i<子串长度时
if(j==0||T.ch[i]==T.ch[j]){ //如果子串为0,或者主串值与子串值相等
++i; //主串与子串皆后移一位
++j;
next[i]=j; //next[j+1]=next[j]
} else { //如果子串不为0,且主串值与子串值不相等
j=next[j]; //令j=next[j],继续循环
}
}
}
//求KMP算法
int index_KMP(const SString& S, const SString& T) {
int next[MAXLEN]; //声明 next数组
get_next(T, next); //将子串T传入 next数组计算值
int i = 1, j = 1; //i为主串位序,j为子串位序
while (i <= S.length && j <= T.length) { //当主串与子串均没有匹配到末尾时
if (j == 0 || S.ch[i] == T.ch[j]) { //如果j=0或者主串值与子串值相等
i++; //主串与子串皆后移一位
j++;
} else { //如果子串不为0,且主串值与子串值不相等
j = next[j]; //子串位序j移动到next[j]所指的位置
}
}
if (j > T.length) //子串位序j移动到末尾+1,即匹配成功
return i - T.length; //返回此时主串匹配部分的首位
else //匹配失败
return -1; //返回-1
}举栗实现
#include <iostream>
#include <string>
#define MAXLEN 25
struct SString {
char ch[MAXLEN];
int length;
};
void initString(SString& s) {
s.length = 0;
s.ch[0] = '\0';
}
void readString(SString& s) {
std::string str;
std::getline(std::cin, str);
for (int i = 0; i < str.length(); i++) {
s.ch[i + 1] = str[i];
s.length++;
}
}
void get_next(const SString& T, int next[]){
int i=1,j=0;
next[1]=0;
while(i<T.length){
if(j==0||T.ch[i]==T.ch[j]){
++i;
++j;
next[i]=j;
} else {
j=next[j];
}
}
}
int index_KMP(const SString& S, const SString& T) {
int next[MAXLEN];
get_next(T, next);
int i = 1, j = 1;
while (i <= S.length && j <= T.length) {
if (j == 0 || S.ch[i] == T.ch[j]) {
i++;
j++;
} else {
j = next[j];
}
}
if (j > T.length)
return i - T.length;
else
return -1;
}
int main() {
SString s1, s2;
initString(s1);
initString(s2);
std::cout << "输入主串: ";
readString(s1);
std::cout << "输入子串: ";
readString(s2);
int pos = index_KMP(s1, s2);
if (pos != -1) {
std::cout << "子串在主串中的位置: " << pos << std::endl;
} else {
std::cout << "未找到匹配位置" << std::endl;
}
return 0;
}
上述程序执行结果如下~

由于避免了主串回溯的问题,KMP 优化算法比朴素的字符串匹配算法更有效。 KMP 优化算法的最坏情况时间复杂度为 O(m+n),其中 m 是模式的长度,n 是文本的长度。
KMP优化算法
算法思想
KMP优化算法是在KMP算法的基础上进行改进,主要优化了next数组的计算方法:
在KMP匹配过程中,循环到不匹配的字符时,虽然不匹配的字符是未知的,但是至少可以确定此处模式串 'j' 指针指向的尾字符与主串 'i' 指针指向的字符不匹配。
如果此处模式串 'j' 指针指向的尾字符与主串 'i' 指针指向的首字符相等,说明主串依然不能匹配该字符,因此可以直接跳过该字符的比较,将指针i向后移动一位~
比较某步骤KMP和KMP优化主指针,如下:

图:串的KMP算法(共3趟)与KMP优化算法举栗比较(共2趟)
为了实现这一优化,KMP优化算法引入了一个新的数组nextval,用于保存字符匹配失败时,子串回溯的位置。
该算法的工作原理如下:
- 初始化两个指针,`i` 和 `j`。 `i` 指向文本中的当前位置,`j` 指向模式中的当前位置。
- 比较 `i` 和 `j` 处的字符。 如果它们相等,则将两个指针向后移动。
- 如果字符不相等,则通过nextval[]获取上一次的回溯位置,并将其赋值给nextval[i],进一步优化主串 `i` 的回溯位置。
- 重复步骤 2 和 3,直到 `i` 到达文本末尾或 `j` 到达模式末尾。
- 如果 j 到达模式的末尾,则该模式已在文本中找到。 该算法返回模式的第一个字符在文本中的位置。
- 如果 `i` 在 `j` 到达模式末尾之前到达文本末尾,则该模式尚未在文本中找到。 该算法返回 -1。
核心代码
//求子串的next值
void get_nextval(const SString& T, int nextval[]) {
int i = 1, j = 0;
nextval[1] = 0;
while (i < T.length) {
if (j == 0 || T.ch[i] == T.ch[j]) { // `i` 和 `j` 处的字符相等,向后移动指针
++i;
++j;
if (T.ch[i] != T.ch[j]) { // 再次递归,直到查找子串j的字符与next j的字符不匹配
nextval[i] = j;
} else {
nextval[i] = nextval[j];
}
} else {
j = nextval[j]; // 令j=nextval[j],继续循环
}
}
}
//求KMP算法
int index_KMP(const SString& S, const SString& T) {
int next[MAXLEN]; //声明 next数组
get_nextval(T, next); //将子串T传入 nextval数组计算值
int i = 1, j = 1; //i为主串位序,j为子串位序
while (i <= S.length && j <= T.length) { //当主串与子串均没有匹配到末尾时
if (j == 0 || S.ch[i] == T.ch[j]) { //如果j=0或者主串值与子串值相等
i++; //主串与子串皆后移一位
j++;
} else { //如果子串不为0,且主串值与子串值不相等
j = next[j]; //子串位序j移动到next[j]所指的位置
}
}
if (j > T.length) //子串位序j移动到末尾+1,即匹配成功
return i - T.length; //返回此时主串匹配部分的首位
else //匹配失败
return -1; //返回-1
}求next数组与nextval数组
推算思路
假设我们有一个子串:"ababaaababaa",求它在KMP算法中的next数组与KMP优化算法中的nextval数组。
在朴素的字符串匹配算法中,我们从主串的第一个字符开始,逐个字符与子串进行比较。如果发现不匹配,我们会回到主串的下一个字符,并重新开始与子串的比较。这种方法的效率不高,特别是在主串和子串相似度高的情况下。
KMP算法通过预处理子串,构建一个部分匹配表(也称为最长前缀后缀表),利用这个表来指导匹配过程。下面是构建next表的步骤:
1)首先,我们观察子串中的每个字符,当前字符未知,找到以当前字符结尾的前1个字符的最长相等前缀和后缀的长度。例如,在子串 "ababaaababaa" 中:
- 以第一个字符 "a" 匹配失败后,子串j的位置重置到j=0,主串右移,相当于子串从第1个字符之前开始匹配。
- 以第二个字符 "b" 匹配失败后,子串j的位置重置到j=1,子串的第1个字符a开始匹配。
- 以第三个字符 "a" 结尾的最长相等前缀和后缀的长度为 0+1(前缀位序1"a"和后缀位序2 "b"并不匹配)。
- 以第四个字符 "b" 结尾的最长相等前缀和后缀的长度为 1+1(前缀位序1"a"和后缀位序3都是 "a")。
- 以第五个字符 "a" 结尾的最长相等前缀和后缀的长度为 2+1(前缀位序1、2和后缀位序3、4都是 "ab")。
- 以第六个字符 "a" 结尾的最长相等前缀和后缀的长度为 3+1(前缀位序1、2、3和后缀位序3、4、5都是 "aba")。
- 以第七个字符 "a" 结尾的最长相等前缀和后缀的长度为 1+1(前缀位序1"a"和后缀位序6都是 "a")。
- 以第八个字符 "b" 结尾的最长相等前缀和后缀的长度为 1+1(前缀位序1"a"和后缀位序7都是 "a")。
- 以第九个字符 "a" 结尾的最长相等前缀和后缀的长度为 2+1(前缀位序1、2和后缀位序7、8都是 "ab")。
- 以第十个字符 "a" 结尾的最长相等前缀和后缀的长度为 3+1(前缀位序1、2、3和后缀位序7、8、9都是 "aba")。
- 以第十一个字符 "a" 结尾的最长相等前缀和后缀的长度为 4+1(前缀位序1、2、3、4和后缀位序7、8、9、10都是 "abab")。
- 以第十二个字符 "a" 结尾的最长相等前缀和后缀的长度为 5+1(前缀位序1、2、3、4\5和后缀位序7、8、9、10、11都是 "ababa")。
2)然后,我们将这些长度填入部分匹配表中。对于子串 "ababaaababaa",对应的部分匹配表如下:
| 字符 | a | b | a | b | a | a | a | b | a | b | a | a |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 指针j 位序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| next[j] 数组 | 0 | 1 | 1 | 2 | 3 | 4 | 2 | 2 | 3 | 4 | 5 | 6 |
3)nextval数组:在next数组匹配时,有时可以确定末尾的元素与前缀一定不是可以匹配的元素~
-
举栗,第五个字符 "a" 结尾的最长相等前缀和后缀的长度为 2+1(前缀位序12与后缀位序34都是 "ab"),但因为在第三轮匹配中,已经可以确定失配的位序5必然为1个不是a的未知数[如果第5位是a,就不会失配]~
-
因此位序3失配,我们再向前查询位序3的nextval值,发现是位序0,已然是到头没有更靠前的元素了~
-
位序3填写0,表示主串指针直接后移,不必再向后匹配子串j~
4)同理,在next数组中,发现next数组所指向位序的元素与现在位序相等的元素时,全部置为前1个位序的next值,完成的表如下所示~
| 字符 | a | b | a | b | a | a | a | b | a | b | a | a |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 指针j 位序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| next[j] 数组 | 0 | 1 | 1 | 2 | 3 | 4 | 2 | 2 | 3 | 4 | 5 | 6 |
| nextval[j] 数组 | 0 | 1 | 0 | 1 | 0 | 4 | 2 | 1 | 0 | 1 | 0 | 4 |
5)无论是KMP算法还是KMP优化算法,只有在文本量大且重复率高时有明显的效率提升,实际应用中暴力朴素算法还是蛮常见的~
结语
博文写得模糊或者有误之处,欢迎小伙伴留言讨论与批评~😶🌫️
码字不易,若有所帮助,可以点赞支持一下博主嘛?感谢~🫡