77 组合

栗子，从 ${1,2,3,4,5,6,7,8,9,10\}$ 中选择4个数：

选择1，从 ${2,3,4,5,6,7,8,9,10\}$ 中选择3个数；
选择2，从 ${3,4,5,6,7,8,9,10\}$ 中选择3个数；
选择3，从 ${4,5,6,7,8,9,10\}$ 中选择3个数；

$\dots$

选择7，从 ${8,9,10}$ 中选择3个数。
选择8，将不足4个数，give up~

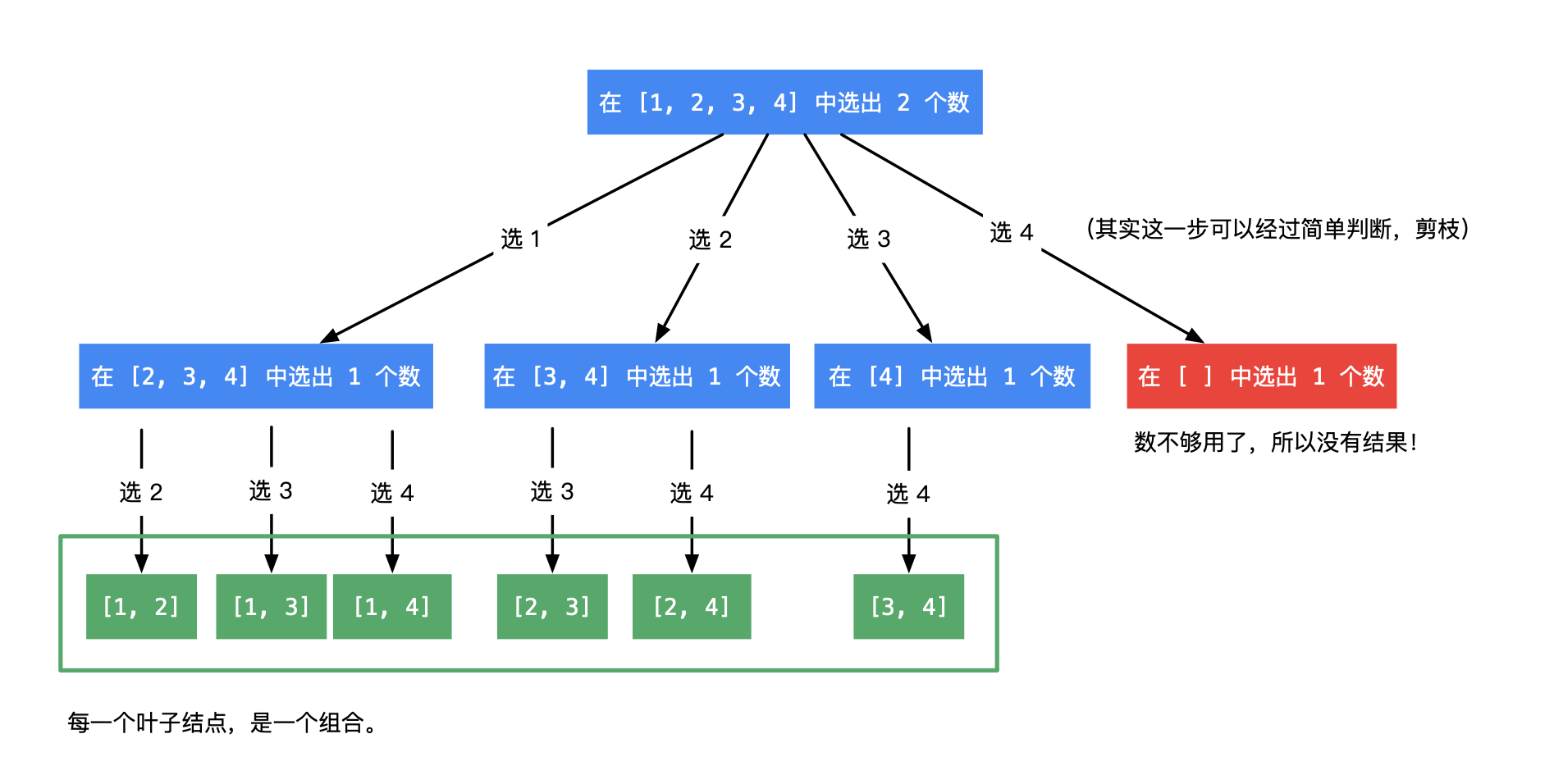
很好，nice，怎么实现呢？

叶子结点的信息体现在从根结点到叶子结点的路径上，因此需要一个表示路径的全局变量 path，path 是一个栈；
同时，需要一个全局变量res存储返回结果；
DFS(int start, int n, int k)表示在[start, n]区间，选取k个数。

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

class Solution {

    // 用于表示经过的路径
    Stack<Integer> path = new Stack<>();
    // 用于返回结果
    List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> combine(int n, int k) {
        DFS(1, n, k);
        return res;
    }

    public void DFS(int start, int n, int k) {
        // 在[start, n]区间，选取k个数
        // 递归终止条件
        if (k == 0) {
            res.add(new ArrayList<>(path));
            return;
        }
        // i最远到[n - k + 1, n]，此时长度为k
        for (int i = start; i <= n - k + 1; i++) {
            // 选择i
            path.push(i);
            // 再从[i + 1, n]选k-1个数
            DFS(i + 1, n, k - 1);
            // 回溯
            path.pop();
        }
    }

}

216 组合总和Ⅲ

类似的思路，不过可以进行一些剪枝：

n > 45，必找不到满足的组合
DFS(int start, int k, int n) ：在[start, 9]中选择k个数，使其和为n
递归终止
- 找到满意的组合：(k == 0 && n == 0)
- 找不到满意的组合了：背包容量不足 || 可用数字额度已用完，但包未装满(n < 0 || k == 0)

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

class Solution {
    Stack<Integer> path = new Stack<>();
    List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> combinationSum3(int k, int n) {
        // 题目描述：找到1-9中的k组合，满足相加等于n
        // 为了不重不漏，还是用相同的方法遍历，含1，不含1含2，……
        if (n > 45) {
            return new ArrayList<>();
        }
        DFS(1, k, n);
        return res;
    }

    public void DFS(int start, int k, int n) {
        // 函数含义：在[start, 9]中选择k个数，使其和为n

        // 1、如果找到了满足的组合
        if (k == 0 && n == 0) {
            res.add(new ArrayList<>(path));
            return;
        }

        // 如果n小于0，说明不可能找到满足的组合啦
        // 如果n大于0且k等于0，没有可用的数字了，但n还没有被消耗完
        if (n < 0 || k == 0) {
            return;
        }

        // 要保证可找范围大于k个数
        // i最大为[10 - K, 9]
        for (int i = start; i <= 10 - k; i++) {
            path.push(i);
            DFS(i + 1, k - 1, n - i);
            path.pop();
        }
    }
}

17 电话号码的字母组合

遍历完整个字符串就可以辣。

import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;

class Solution {
    HashMap<Character, char[]> phone = new HashMap<Character, char[]>() {{
        put('2', new char[]{'a', 'b', 'c'});
        put('3', new char[]{'d', 'e', 'f'});
        put('4', new char[]{'g', 'h', 'i'});
        put('5', new char[]{'j', 'k', 'l'});
        put('6', new char[]{'m', 'n', 'o'});
        put('7', new char[]{'p', 'q', 'r', 's'});
        put('8', new char[]{'t', 'u', 'v'});
        put('9', new char[]{'w', 'x', 'y', 'z'});
    }};

    StringBuilder path = new StringBuilder();
    List<String> res = new ArrayList<>();

    public List<String> letterCombinations(String digits) {
        if ("".equals(digits)) {
            return res;
        }
        DFS(digits.toCharArray(), 0);
        return res;
    }

    public void DFS(char[] digits, int i) {
        // 从第i个字母开始的digits数组，可以获得多少种ans
        if (i == digits.length) {
            res.add(path.toString());
            return;
        }
        char num = digits[i];
        for (char alpha: phone.get(num)) {
            path.append(alpha);
            DFS(digits, i + 1);
            path.deleteCharAt(i);
        }
    }
}

39 组合总和

【2】限制：数字可以重复使用，但不能生成重复组合。

回溯树的样子有所改变：

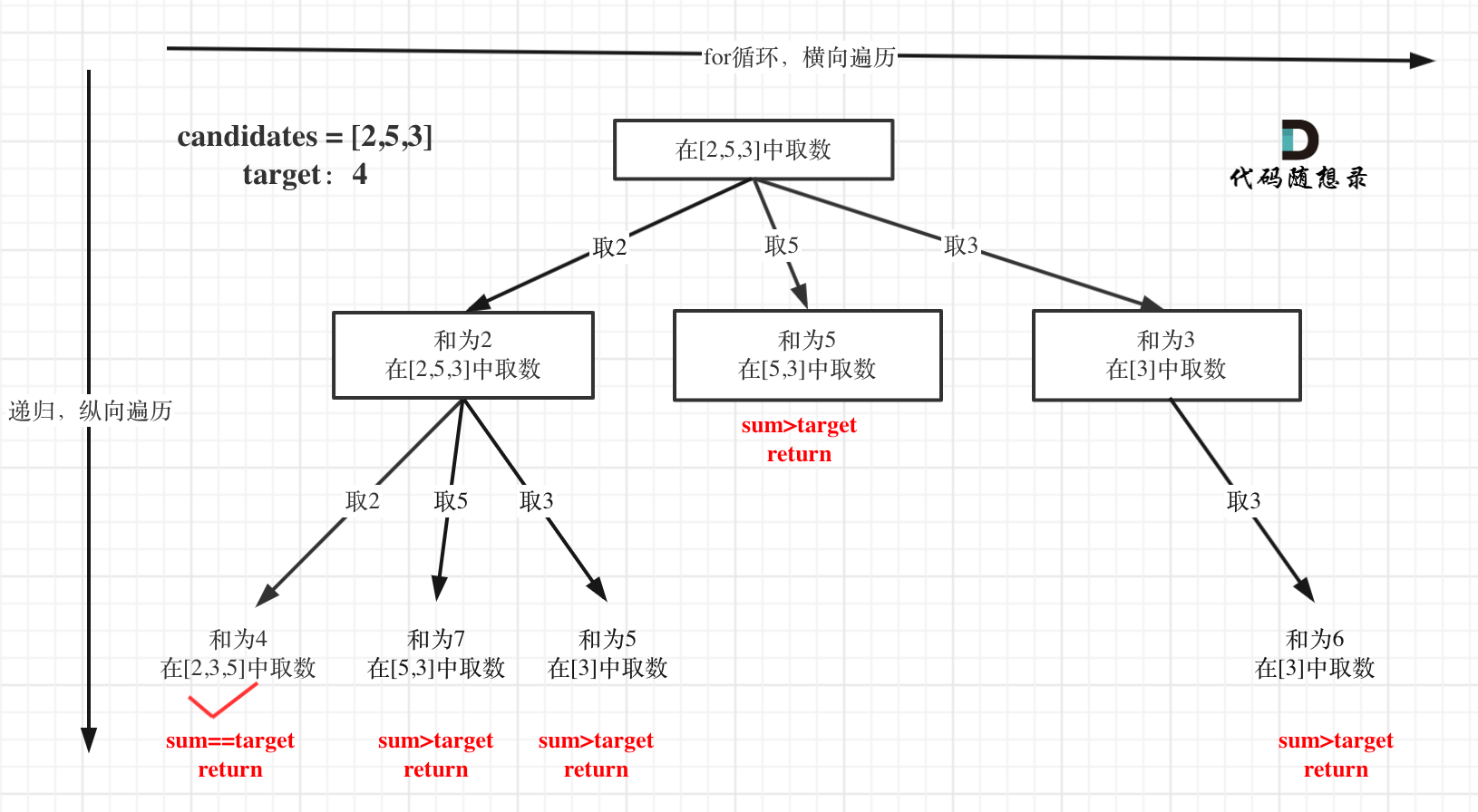
39.组合总和

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

class Solution {
    Stack<Integer> path = new Stack<>();
    List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        // candidates不重复
        DFS(candidates, 0, target);
        return res;
    }

    public void DFS(int[] candidates, int start, int target) {
        // 可选candidates[start:]的数字，组合为target
        if (target == 0) {
            res.add(new ArrayList<>(path));
            return;
        }
        if (target < 0 || start == candidates.length) {
            return;
        }

        // 如果选择该数字的话，下一步仍可选择该位置数字
        path.push(candidates[start]);
        DFS(candidates, start, target - candidates[start]);
        path.pop();
        // 不选择该位置数字的话，下一步就要往下移动
        DFS(candidates, start + 1, target);
    }
}

40 组合总和Ⅱ★

【3】限制：数字可以重复使用，但不能生成重复组合。

提供的可选数组列表有重复。

根据上一题可知，应该限制同一个数字的树枝最多向下 $f re q$ 次。

采用和三数之和类似的思路，第一个元素应该是不同的元素。

剪枝：若candidates[i] > target，之后的情况可直接不用考虑。

去重：

// 如果不是第一个start位置的数字
// 并且和前一个数字相等，由于前一个数字已经向下扩展过了，这个树枝就不必再扩展哩（参考三数之和思路
if (i > start && candidates[i] == candidates[i - 1]) {
    continue;
}

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Stack;

class Solution {
    Stack<Integer> combination = new Stack<>();
    List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);
        DFS(candidates, 0, target);
        return res;
    }

    public void DFS (int[] candidates, int start, int target) {
        // 含义：从candidates[start:]找到和为target的组合

        // 如果target降到0，说明找到了这样的组合
        if (target == 0) {
            res.add(new ArrayList<>(combination));
            return;
        }

        // 如果target < 0或者走到了尽头, 剪枝
        if (target < 0 || start == candidates.length) {
            return;
        }

        // 这个for循环代表了同一层的递归树,
        // 如果遍历到某个值时大于target，不必再向下考虑，剪枝
        for (int i = start; i < candidates.length && candidates[i] <= target; i++) {
            
            // 如果和前一个数字相等，由于前一个数字已经向下扩展过了，这个树枝就不必再扩展哩
            if (i > start && candidates[i] == candidates[i - 1]) {
                continue;
            }

            // 选择start位置
            combination.push(candidates[i]);
            DFS(candidates, i + 1, target - candidates[i]);
            combination.pop();
        }

    }
}