Leetcode周赛348

news2024/11/24 3:58:00

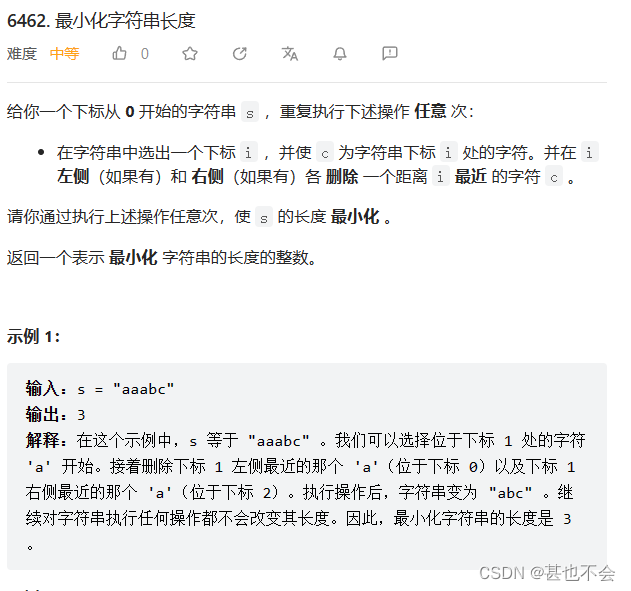
第一题：最小化字符串长度

在这里插入图片描述
思路分析

通过分析我们可以发现，只要存在重复的元素就可以继续进行操作
所以这里本质上是一道去重的题目
去重我们可以使用双指针算法和Set；我们选择使用Set进行去重

class Solution {
    public int minimizedStringLength(String s) {
        if(s.length()==0)return 0;
        char[] ch=s.toCharArray();
        Set<Character> set=new HashSet<>();
        for(char c:ch){
            set.add(c);
        }
        return set.size();

    }
}

第二题：半有序排列

在这里插入图片描述
思路分析

通过分析我们可以发现1和n有两种位置关系
情况1：-1在n的左边：1向前交换，n向后交换互不影响;

移动次数与1和n的下标有关，我们不难发现 1移动次数与其下标相等，n移动次数为n-1-index_n,答案为 $index_1+(n-1)-index_n$
情况2：- 1在n的右边：1在向前交换时，会将n向后移动一次 ,也就是其结果比上述描述的答案少1次为 $index_1+(n-1)-index_n-1$

class Solution {
    public int semiOrderedPermutation(int[] nums) {
        int n=nums.length;
        int res=1;
        int index_1=0;//用来记录1的下标
        int index_n=n-1;//用来记录n的下标
        //特判
        if(nums[index_1]==1 && nums[index_n]==n)return 0;
        //寻找两个点的坐标
        for(int i=0;i<n;i++){
            if(nums[i]==1)index_1=i;
            if(nums[i]==n)index_n=i;
        }
        if(index_1<index_n)return (index_1+(n-index_n-1));//情况1
        if(index_1>index_n)return (index_1+(n-index_n-2));//情况2
        return 0;
    }
}

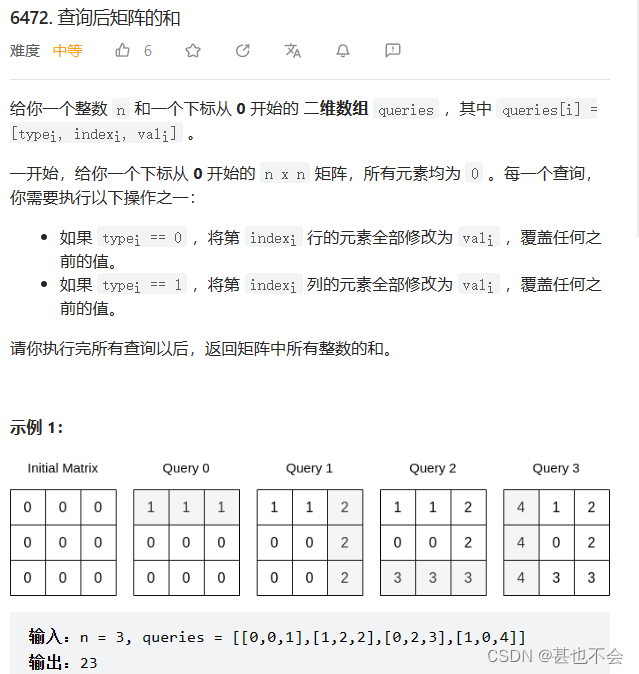
day3 查询后矩阵和

在这里插入图片描述
思路分析

不难发现

如果对某行，某列重复操作多次，只有最后一次会影响答案，所以我们进行倒序遍历（将重复操作去除）
（已经去除的情况下）后面的行操作，会将前面已经操作过的列集合，每列都覆盖一个数字
列同理会覆盖前面的行

class Solution {
    public long matrixSumQueries(int n, int[][] queries) {
        Set<Integer> sr=new HashSet<>();//存储操作过的列
        Set<Integer> sc=new HashSet<>();//存储操作过的列
        long res=0;
        //倒序遍历queries
        for(int i=queries.length-1;i>=0;i--){
            int[] q=queries[i];
            int type=q[0];
            int index=q[1];
            int val=q[2];
            if(type==0){//对行操作
                if(sr.contains(index))continue;
                else{
                    res+=val*(n-sc.size());
                    sr.add(index);
                } 
            }else{//d对列操作
                if(sc.contains(index))continue;
                else{
                    res+=val*(n-sr.size());
                    sc.add(index);
                } 
            }
        }
        return res;
    }
}