3.要求与任务

从 1790 — 1990 年间美国每隔 10 年的人口记录如下表所示：

用以上数据检验马尔萨斯 ( Malthus)人口指数增长模型，根据检验结果进一步讨论马尔萨斯
人口模型的改进，并利用至少两种模型来预测美国2010 年的人口数量。
提示 1 ： Malthus 模型的基本假设是：人口的增长率为常数，记为 r 。记时刻 t的人口为
x ( t )（即 x ( t )为模型的状态变量），且初始时刻的人口为 ，于是得到如下微分方程：

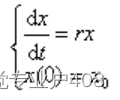
提示 2 ：阻滞增长模型（或 Logistic 模型） 由于资源、环境等因素对人口增长的阻滞作用，
人口增长到一定数量后，增长率会下降，假设 人口的增长率为x 的减函数，如设 r(x)=r(1-x/xm) ，
其中 r 为固有增长率 (x 很小时 ) ，xm为人口容量（资源、环境能容纳的最大数量）， 于是得到
如下微分方程：

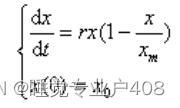
4、代码及结果
方法一：马尔萨斯 ( Malthus)人口指数增长模型
代码：

t = [1790 1800 1810 1820 1830 1840 1850 1860 1870 1880 1890 1900 1910 1920 1930 1940 1950 1960 1970 1980 1990];
p = [3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 106.5 123.2 131.7 150.7 179.3 204.0 226.5 251.4];
y = log(p); %求ln(p)函数值
a = polyfit(t,y,1) %用一次多项式对t和y进行拟合
z = polyval(a,t); %求得以a为系数的多项式在t处的函数值
z1 = exp(z)
r = a(1)
plot(t,p,'bo',t,z1,'r') %分别画出散点图以及拟合曲线图
xlabel('时间');
ylabel('人口数量');
legend('实际数据','理论曲线');

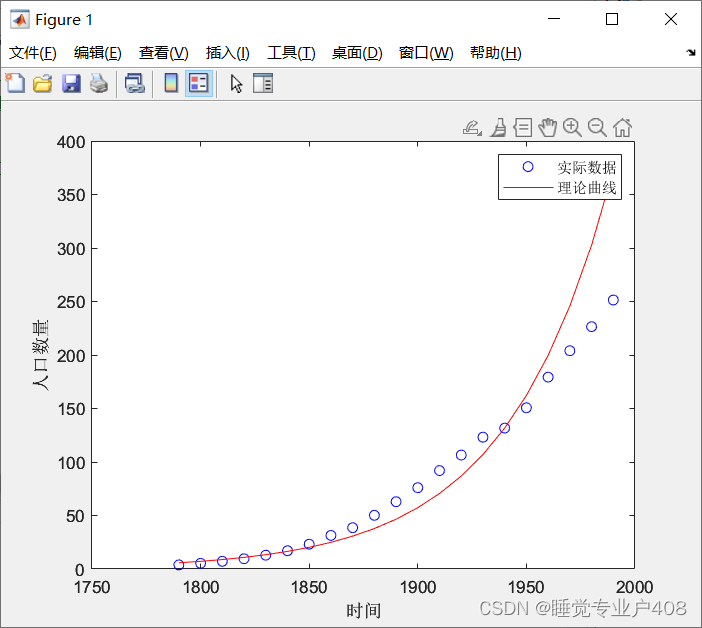
结论：随着时间的增加，人口按指数规律无限增长。可以进行短期的人口预测，较为符合
但是之后误差就很大了。
误差分析：询美国人口统计图表得出2000年为282.162、2010年人口为309.322、2020年人口
为329.484，发现两者有一定区别，因为预测中无法考虑到未来可能发生的各种变化因素。实际上
随着人口数量的增加，自然资源、环境因素， 人口政策，年龄和性别结构、地域特征等因素对人
口数量的阻滞作用越来越明显。
方法二：Logistic模型
通过求解差分方程的方式得到每个时刻的人口增长率，并将其归一化。接着使用线性回归的方法拟合出人口增长率与人口数量之间的关系，并推导出了一个基于人口增长率的指数模型，用于预测未来的人口数量。
代码：

clc
clear
close all
x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 106.5 123.2 131.7 150.7 179.3 204.0 226.5 251.4];%人口
n=length(x);
t=0:1:n-1;
rk=zeros(1,n);
rk(1)=(-3*x(1)+4*x(2)-x(3))/2;
rk(n)=(x(n-2)-4*x(n-1)+3*x(n))/2;
for i=2:n-1
    rk(i)=(x(i+1)-x(i-1))/2;
end
rk=rk./x;
p=polyfit(x,rk,1);
b=p(2);
a=p(1);
r0=b;
xm=-r0/a;
%输出
pnum=zeros(n,1);
for i=0:1:n-1
    pnum(i+1)=xm/(1+(xm/x(1)-1)*exp(-r0*i));
end
year1=[1790 1840 1850 1860 1870 1880 1890 1900 1910 1920 1930 1940 1950 1960 1970 1980 1990 2000 2010 2020 2021];
plot(year1,pnum,'r--o',year1,x,'k-*')
xlabel('年份')
ylabel('人口数量/万人')
legend('预测人口数量','实际人口数量')

figure(2)
fnum=zeros(n+14,1);
for i=0:1:n+13
    fnum(i+1)=xm/(1+(xm/x(1)-1)*exp(-r0*i));
end
year2=[1790 1840 1850 1860 1870 1880 1890 1900 1910 1920 1930 1940 1950 1960 1970 1980 1990 2000 2010 2020 2021 2022 2023 2024 2025 2026 2027 2028 2029 2030 2031 2032 2033 2034 2035];
plot(year2,fnum,'r--o')
xlabel('年份')
ylabel('人口数量/万人')
legend('预测人口数量')

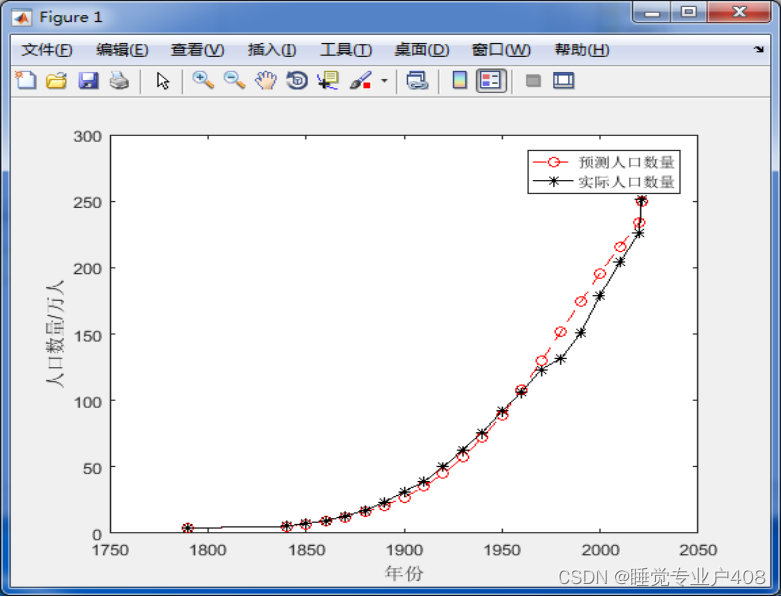
结论：当t=2000 时人口为295.769、t=2010时人口为315.909、t=2020时人口为333.962。
误差分析：查询美国人口统计图表得出2000年为282.162、2010年人口为309.322、2020年人口
为329.484，发现两者几乎一致，Logistic模型的缺点是模型中的参数r和人口总数上限xm很难准确得
到，尤其是xm的值还会随着人口发展变化的情况而改变。实际上随着人口数量的增加，自然资源、环境因素， 人口政策，
年龄和性别结构、地域特征等因素对人口 数量的阻滞作用越来越明显，增长率不应取为常数。
方法三：多项式拟合
在代码中，使用了polyfit函数拟合5阶多项式，将拟合结果和原始数据一起绘制出来。另外，该
代码还用polyval函数计算了未来几十年的人口预测数量，并在另一个图表中绘制出来。
代码：

Close；
clc;
clear all           %清除所有
n=5;%拟合多项式的次数
year=[1790 1800 1810 1820 1830 1840 1850 1860 1870 1880 1890 1900 1910 
1920 1930 1940 1950 1960 1970 1980 1990];
num=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 106.5
 123.2 131.7 150.7 179.3 204.0 226.5 251.4];%户籍人口; 
p5= polyfit(year,num,n);       %5阶拟合 
%绘制原始数据和拟合曲线图
figure(1)
hold on;
xlabel('year');     %设置横坐标名
ylabel('num');      %设置纵坐标名
title('1790-1990人口增长曲线');   %设置标题
grid on      %网格线
plot(year,num,'r*',year,polyval(p5,year)) 
legend('人口数量','拟合曲线')
figure(2)
year1=[1790 1800 1810 1820 1830 1840 1850 1860 1870 1880 1890 1900 1910 
1920 1930 1940 1950 1960 1970 1980 1990 2000 2010 2020 2030]
plot(year1,polyval(p5,year1)) 
people=polyval(p5,year1);
legend('人口预测数量')

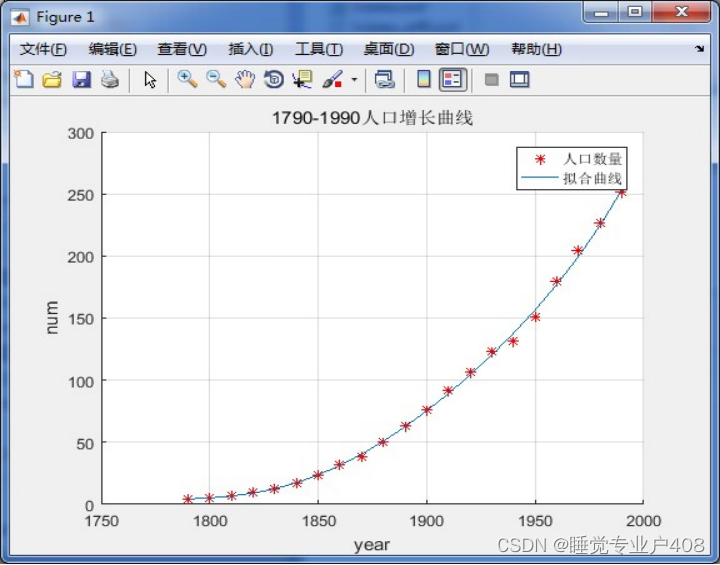
结论：当t=2000 时人口为286.151、t=2010时人口为323.925、t=2020时人口为369.047。
误差分析：查询美国人口统计图表得出2000年为282.162、2010年人口为309.322、2020年人口
为329.484发现两者有一些差别，而且预测的时间越长，误差会逐渐增大，因为预测中无法考虑到
未来可能发生的各种变化因素。实际上随着人口数量的增加，自然资源、环境因素， 人口政策，
年龄和性别结构、地域特征等因素对人口数量的阻滞作用越来越明显，增长率不应取为常数。
四、总结及体会
通过这个数学建模的实例，我们可以体会到数学建模的重要性和难度。
在实际问题中，我们需要根据已知数据、假设和条件，将其量化为数学模型。经过推导和求解，得出模型所能提
供的结果。这个过程需要严谨的数学思维和运用一定的数学工具。
同时，在实际问题中，还需要考虑到数据的准确性、假设的合理性和模型的可靠性等因素。这些因素都会影响到
最终的模型结果和应用效果。因此，需要在建立模型的过程中，注重数据的采集、分析和处理，以及对假设和模
型的合理性进行判断和修正。
此外，我们还需要在建模的过程中，注重交流和合作。不同领域的专家拥有不同的知识背景和专业技能，他
们的合作和交流可以使得模型更加完善和全面。
总之，数学建模不仅是数学的一个应用领域，同时也涉及到多个学科，需要全面的知识储备和跨学科的合作
在实际问题中，需要注重思维方式、数据准确性和交流合作等因素，以期获得可信、可靠的模型结果。