文章目录
- 1、树
- 2、二叉树
- 3、满二叉树
- 4、完全二叉树
- 5、二叉树的遍历(前序、中序、后序)
- 二叉树删除节点或树
- 6、顺序存储二叉树
- 顺序存储二叉树遍历(前序、中序、后序)
- 7、线索化二叉树
- 中序线索二叉树
- 前序线索二叉树
- 后序线索二叉树
1、树
树是一种非线性的数据结构,是由n(n >=0)个结点组成的有限集合
如果n=0,树为空树。
如果n>0,除根节点外,其余结点被分成m(m>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。
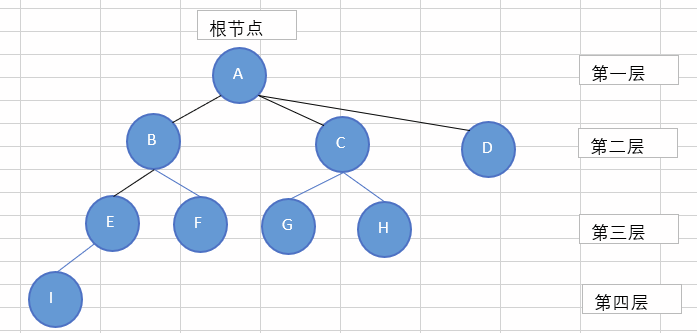
相关概念:
- 根节点:没有父节点的节点。
- 叶节点:没有子节点的节点。
- 兄弟节点:具有相同父节点的节点;
- 结点的度:结点拥有的子树个数。例如A节点的度3。 B,C为2
- 树的度:树内各结点最大的度 。例如A节点的度最大,所以树的度为3
- 节点的层次 :从根开始定义起,根为第 1 层,根的子节点为第 2 层,以此类推;
- 树的高度或深度 :树中节点的最大层次; 如上图:树的高度为 4
- 森林 :由 m( m>0 )棵互不相交的树的集合称为森林。
2、二叉树
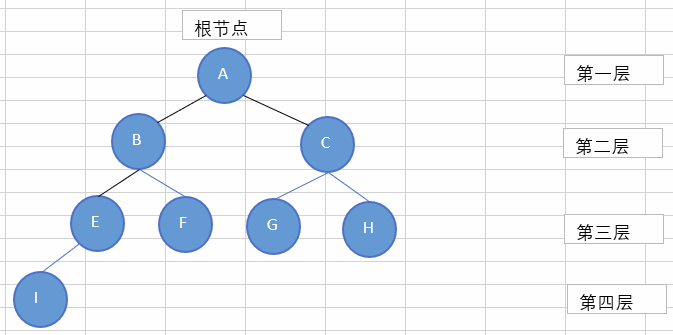
二叉树(Binary tree)是每个节点最多有两个子节点的树。(删掉上面的D节点)
3、满二叉树
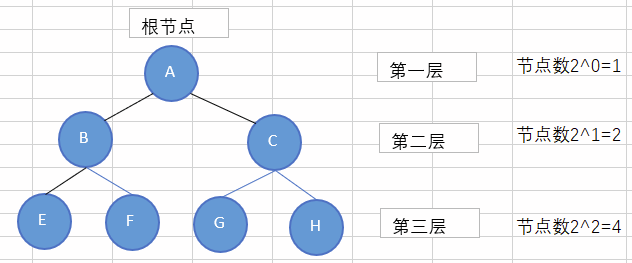
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。
如果一个二叉树的层数为n,且结点总数是2^n -1 ,则它就是满二叉树
4、完全二叉树
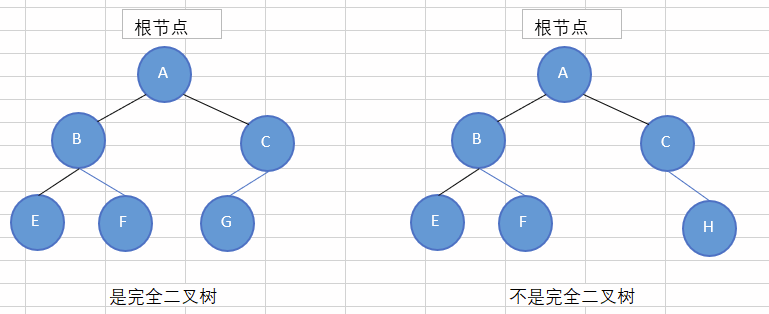
完全二叉树是一种特殊的二叉树,它除了最后一层外,其他每一层都被完全填满,且最后一层的节点都靠左排列。
满二叉树一定是完全二叉树
5、二叉树的遍历(前序、中序、后序)
按照不同的规则(看输出父节点的顺序)分为:
-
前序遍历:先输出父节点,再遍历左子树,后右子树
-
中序遍历:先遍历左子树,再输出父节点,再遍历右子树
-
后序遍历:先遍历左子树,再遍历右子树,最后输出父节点
例如上面的完全二叉树: 前序遍历:ABEFCG 中序遍历:EBFAGC 后序遍历:EFBGCA
代码实现:
package Tree;
public class BinaryTreeDemo {
public static void main(String[] args) {
BinaryTree binaryTree = new BinaryTree();
Node a = new Node("A");
Node b = new Node("B");
Node c = new Node("C");
Node e = new Node("E");
Node f = new Node("F");
Node g = new Node("G");
//手动创建树
binaryTree.setRoot(a);
a.left=b;
a.right=c;
b.left=e;
b.right=f;
c.left=g;
System.out.println("前序遍历:");
binaryTree.preOrderM();
System.out.println("中序遍历:");
binaryTree.infixOrderM();
System.out.println("后序遍历:");
binaryTree.postOrderM();
}
}
//创建树的属性和方法
class BinaryTree{
//定义根节点
Node root;
public void setRoot(Node root) {
this.root = root;
}
//前序遍历
public void preOrderM() {
if (this.root != null) {
this.root.preOrder();
} else {
System.out.println("二叉树为空!无法遍历!");
}
}
//中序遍历
public void infixOrderM() {
if (this.root != null) {
this.root.infixOrder();
} else {
System.out.println("二叉树为空!无法遍历!");
}
}
//中序遍历
public void postOrderM() {
if (this.root != null) {
this.root.postOrder();
} else {
System.out.println("二叉树为空!无法遍历!");
}
}
}
//创建节点对象的属性和方法
class Node{
String name;
Node left;
Node right;
public Node(String name) {
this.name = name;
}
//重写toString方法
@Override
public String toString() {
return "Node{" +
"name='" + name + '\'' +
'}';
}
//前序遍历
public void preOrder(){
//先打印父节点
System.out.println(this);
if (this.left!=null){
this.left.preOrder();
}
if (this.right!=null){
this.right.preOrder();
}
}
public void infixOrder() {
//先进行左树遍历
if (this.left!=null){
this.left.infixOrder();
}
System.out.println(this);
if (this.right!=null){
this.right.infixOrder();
}
}
public void postOrder() {
//先进行左树遍历
if (this.left!=null){
this.left.postOrder();
}
if (this.right!=null){
this.right.postOrder();
}
System.out.println(this);
}
}
| 前序遍历 | 中序遍历 | 后序遍历 |
|---|---|---|
 |  |  |
二叉树删除节点或树
- 如果删除的节点是叶子节点,则删除该节点
- 如果删除的节点是非叶子节点,则删除该子树
代码实现:删除树B和叶节点E
package Tree;
public class BinaryTreeDemo {
public static void main(String[] args) {
BinaryTree binaryTree = new BinaryTree();
Node a = new Node("A");
Node b = new Node("B");
Node c = new Node("C");
Node e = new Node("E");
Node f = new Node("F");
Node g = new Node("G");
//手动创建树
binaryTree.setRoot(a);
a.left=b;
a.right=c;
b.left=e;
b.right=f;
c.left=g;
System.out.println("前序遍历:");
binaryTree.preOrderM();
//删除某个节点
System.out.println("删除节点E");
binaryTree.deleteNode("E");
System.out.println("查看删除后的节点");
binaryTree.preOrderM();
System.out.println("删除树B");
binaryTree.deleteNode("B");
System.out.println("查看删除后的节点");
binaryTree.preOrderM();
}
}
//创建树的属性和方法
class BinaryTree{
//定义根节点
Node root;
public void setRoot(Node root) {
this.root = root;
}
//前序遍历
public void preOrderM() {
if (this.root != null) {
this.root.preOrder();
} else {
System.out.println("二叉树为空!无法遍历!");
}
}
//中序遍历
public void infixOrderM() {
if (this.root != null) {
this.root.infixOrder();
} else {
System.out.println("二叉树为空!无法遍历!");
}
}
//中序遍历
public void postOrderM() {
if (this.root != null) {
this.root.postOrder();
} else {
System.out.println("二叉树为空!无法遍历!");
}
}
//删除节点,先判断根节点是不是所需要的节点
public void deleteNode(String name){
if (this.root!=null){
if (this.root.name==name){
this.root=null;
}else {
this.root.delNode(name);
}
}else {
System.out.println("二叉树为空!无法删除节点");
}
}
}
//创建节点对象的属性和方法
class Node{
String name;
Node left;
Node right;
public Node(String name) {
this.name = name;
}
//重写toString方法
@Override
public String toString() {
return "Node{" +
"name='" + name + '\'' +
'}';
}
//前序遍历
public void preOrder(){
//先打印父节点
System.out.println(this);
if (this.left!=null){
this.left.preOrder();
}
if (this.right!=null){
this.right.preOrder();
}
}
public void infixOrder() {
//先进行左树遍历
if (this.left!=null){
this.left.infixOrder();
}
System.out.println(this);
if (this.right!=null){
this.right.infixOrder();
}
}
public void postOrder() {
//先进行左树遍历
if (this.left!=null){
this.left.postOrder();
}
if (this.right!=null){
this.right.postOrder();
}
System.out.println(this);
}
//删除node方法
public void delNode(String name) {
if (this.left!=null&&this.left.name==name){
this.left=null;
return;
}
if (this.right!=null&&this.right.name==name){
this.right=null;
return;
}
//上述是root底下的两个节点。若这两个都不是我们要的那个节点,需再递归
if (this.left!=null){
this.left.delNode(name);
}
if (this.right!=null){
this.right.delNode(name);
}
}
}
6、顺序存储二叉树
顺序存储二叉树是二叉树的一种存储方式。
将二叉树存储在一个数组中,通过存储元素的下标反映元素之间的父子关系。
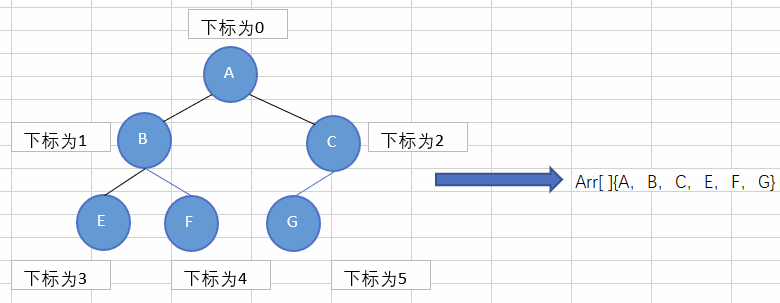
特点:
- 顺序存储二叉树通常只考虑完全二叉树
- 遍历数组arr时,仍然可以(前序、中序、后序遍历)
- 下标为n的元素的左子节点下标为2*n+1
- 下标为n的元素的右子节点下标为2*n+2
- 下标为n的元素的父节点为(n-1)/2
顺序存储二叉树遍历(前序、中序、后序)
public class ArrayBinaryTreeDemo {
public static void main(String[] args) {
String [] arr={"A","B","C","E","F","G"};
ArrayBinaryTree tree = new ArrayBinaryTree(arr);
tree.preOrder();
System.out.println();
tree.infixOrder();
System.out.println();
tree.postOrder();
}
}
//实现顺序存储二叉树
class ArrayBinaryTree{
String[] arr;
public ArrayBinaryTree(String[] arr) {
this.arr = arr;
}
public void preOrder(){
this.preOrder(0);
}
public void infixOrder(){
this.infixOrder(0);
}
public void postOrder(){
this.postOrder(0);
}
//实现前序遍历
public void preOrder(int index){
if (arr==null || arr.length==0){
System.out.println("数组为空");
return;
}
System.out.print(arr[index]+" ");
if ((index * 2 + 1) < arr.length) {
preOrder(index * 2 + 1);
}
//再递归右子树
if ((index * 2 + 2) < arr.length) {
preOrder(index * 2 + 2);
}
}
//实现中序遍历
public void infixOrder(int index){
if (arr==null || arr.length==0){
System.out.println("数组为空");
return;
}
if ((index * 2 + 1) < arr.length) {
infixOrder(index * 2 + 1);
}
System.out.print(arr[index]+" ");
//再递归右子树
if ((index * 2 + 2) < arr.length) {
infixOrder(index * 2 + 2);
}
}
//后序遍历
public void postOrder(int index){
if (arr==null || arr.length==0){
System.out.println("数组为空");
return;
}
if ((index * 2 + 1) < arr.length) {
postOrder(index * 2 + 1);
}
//再递归右子树
if ((index * 2 + 2) < arr.length) {
postOrder(index * 2 + 2);
}
System.out.print(arr[index]+" ");
}
}
运行结果:

7、线索化二叉树
对于n个结点的二叉树,在二叉链存储结构中有n+1个空链域,利用这些空链域存放在某种遍历次序下该结点的前驱结点和后继结点的指针,这些指针称为线索,加上线索的二叉树称为线索二叉树。
根据线索性质的不同,线索二叉树可分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种。
注意:线索链表解决了无法直接找到该结点在某种遍历序列中的前驱和后继结点的问题,解决了二叉链表找左、右孩子困难的问题。
遍历线索化二叉树:因为线索化后,各个结点指向有变化,因此原来的遍历方式不能使用,这时需要使用新的方式遍历线索化二叉树,各个节点可以通过线型方式遍历,因此无需使用递归方式,这样也提高了遍历的效率。
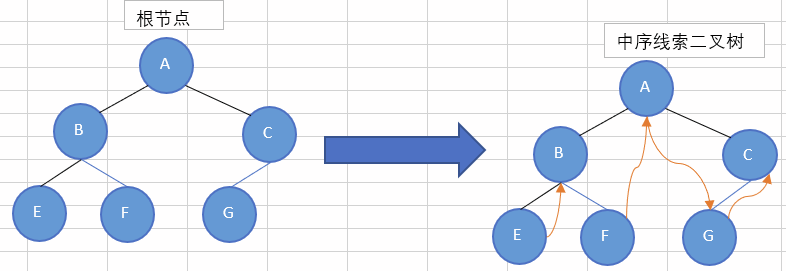
中序线索二叉树
例如:中序线索二叉树
public class ThreadedBinaryTreeDemo {
public static void main(String[] args) {
ThreadedBinaryTree threadedBinaryTree = new ThreadedBinaryTree();
MyNode a = new MyNode("A");
MyNode b = new MyNode("B");
MyNode c = new MyNode("C");
MyNode e = new MyNode("E");
MyNode f = new MyNode("F");
MyNode g = new MyNode("G");
//手动创建树
threadedBinaryTree.setRoot(a);
a.left=b;
a.right=c;
b.left=e;
b.right=f;
c.left=g;
System.out.println("未线索化前e节点的前驱节点和后驱");
System.out.println("F号结点的前驱结点为:"+e.left);//3
System.out.println("F号结点的后继结点为:"+e.right);//1
System.out.println("中序线索化后e节点的前驱节点和后驱");
threadedBinaryTree.infixThreadedNodes();
System.out.println("F号结点的前驱结点为:"+e.left);//3
System.out.println("F号结点的后继结点为:"+e.right);//1
}
}
//定义能实现线索化的二叉树
class ThreadedBinaryTree {
MyNode root;
MyNode pre=null;//指向当前节点的前驱节点 递归过程中pre总是保留前一个节点
//为了实现线索化,需要创建指向当前节点的前驱结点的指针
public void setRoot(MyNode root) {
this.root = root;
}
public void infixThreadedNodes() {
this.infixThreadedNodes(root);
}
//编写对二叉树进行中序线索化的方法
public void infixThreadedNodes(MyNode node) {
if (node == null) {//节点为空 不能线索化
return;
}
//线索化左子树
infixThreadedNodes(node.left);
if (node.left==null){
node.left=pre;
node.leftType=1;
}
//处理后继节点
if (pre!=null && pre.right==null){
pre.right=node;
pre.rightType=1;
}
//每处理一个节点,让当前节点是下一个节点的前驱节点
pre=node;
//线索化右子树
infixThreadedNodes(node.right);
}
}
class MyNode{
String name;
MyNode left;
MyNode right;
//说明
//1.如果leftType==0 表示指向的是左子树,为1 表示指向前驱节点
//2.如果rightType==0 表示指向的是右子树,为1 表示指向后继节点
int leftType;
int rightType;
public MyNode(String name) {
this.name = name;
}
//重写toString方法
@Override
public String toString() {
return "Node{" +
"name='" + name + '\'' +
'}';
}
}
运行结果:

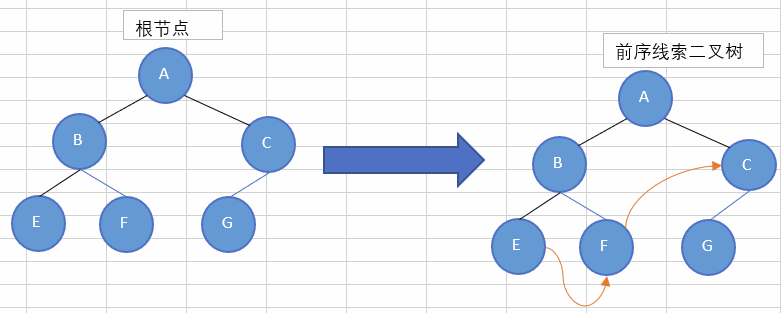
前序线索二叉树
//编写对二叉树进行前序线索化的方法
public void preThreadedNodes(MyNode node) {
if (node == null) {
return;
}
//线索化当前节点
//处理前驱节点 左指针为空 则将左指针指向前驱节点
if (node.left == null) {
node.left=pre;
node.leftType=1;
}
//处理后继节点 前一个节点的后继节点指向当前节点
if (pre != null && pre.right == null) {
pre.right=node;
pre.rightType=1;
}
//更新pre
pre = node;
//线索化左子树
if (node.leftType == 0) {
preThreadedNodes(node.left);
}
//线索化右子树
if (node.rightType == 0) {
preThreadedNodes(node.right);
}
}

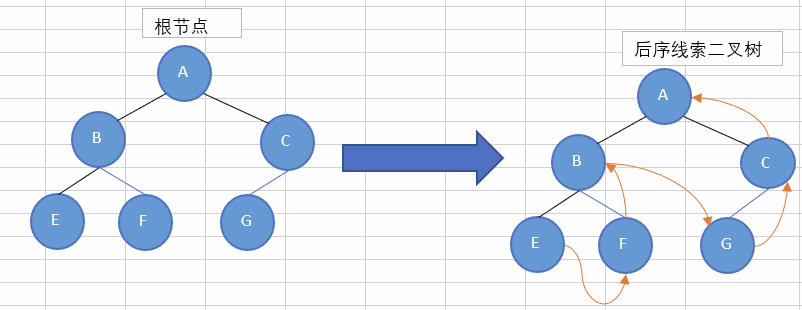
后序线索二叉树
//编写对二叉树进行后序线索化的方法
public void postThreadedNodes(MyNode node) {
if (node == null) {
return;
}
//线索化左子树
if (node.leftType == 0) {
postThreadedNodes(node.left);
}
//线索化右子树
if (node.rightType == 0) {
postThreadedNodes(node.right);
}
//线索化当前节点
if (node.left == null) {
node.left=pre;
node.leftType=1;
}
if (pre != null && pre.right == null) {
pre.right=node;
pre.rightType=1;
}
//更新pre
pre = node;
}







![[BUUOJ] [RE] [ACTF新生赛2020] rome1](https://img-blog.csdnimg.cn/cbc76794d3094d46b6052ce3c7eccfd1.png)