2716. 最小化字符串长度

题目描述

描述：给你一个下标从 0 开始的字符串 s ，重复执行下述操作 任意 次：

在字符串中选出一个下标 i ，并使 c 为字符串下标 i 处的字符。并在 i 左侧（如果有）和 右侧（如果有）各 删除 一个距离 i 最近 的字符 c 。
请你通过执行上述操作任意次，使 s 的长度 最小化 。

返回一个表示 最小化 字符串的长度的整数。

示例 1：

输入：s = "aaabc"
输出：3
解释：在这个示例中，s 等于 "aaabc" 。我们可以选择位于下标 1 处的字符 'a' 开始。接着删除下标 1 左侧最近的那个 'a'（位于下标 0）以及下标 1 右侧最近的那个 'a'（位于下标 2）。执行操作后，字符串变为 "abc" 。继续对字符串执行任何操作都不会改变其长度。因此，最小化字符串的长度是 3 。

示例 2：

输入：s = "cbbd"
输出：3
解释：我们可以选择位于下标 1 处的字符 'b' 开始。下标 1 左侧不存在字符 'b' ，但右侧存在一个字符 'b'（位于下标 2），所以会删除位于下标 2 的字符 'b' 。执行操作后，字符串变为 "cbd" 。继续对字符串执行任何操作都不会改变其长度。因此，最小化字符串的长度是 3 。

示例 3：

输入：s = "dddaaa"
输出：2
解释：我们可以选择位于下标 1 处的字符 'd' 开始。接着删除下标 1 左侧最近的那个 'd'（位于下标 0）以及下标 1 右侧最近的那个 'd'（位于下标 2）。执行操作后，字符串变为 "daaa" 。继续对新字符串执行操作，可以选择位于下标 2 的字符 'a' 。接着删除下标 2 左侧最近的那个 'a'（位于下标 1）以及下标 2 右侧最近的那个 'a'（位于下标 3）。执行操作后，字符串变为 "da" 。继续对字符串执行任何操作都不会改变其长度。因此，最小化字符串的长度是 2 。

提示：

1 <= s.length <= 100
s 仅由小写英文字母组成

解题思路

难度：简单。

思路：最直观的想法是，虽然题目描述这么复杂，但是本质上是求字符串中不重复的字符数。使用set即可。

int minimizedStringLength(string s) {
        int n=s.size();
        unordered_set<char> ump;
        for(int i=0;i<n;i++)
        {
            if(ump.count(s[i])==0)
                ump.emplace(s[i]);
        }
        return ump.size();
    }

总结：有时候题目描述较长不要害怕，不要被题目所迷惑，换个角度思考。

2717. 半有序排列

题目描述

描述：给你一个下标从 0 开始、长度为 n 的整数排列 nums 。

如果排列的第一个数字等于 1 且最后一个数字等于 n ，则称其为 半有序排列 。你可以执行多次下述操作，直到将 nums 变成一个 半有序排列 ：

选择 nums 中相邻的两个元素，然后交换它们。
返回使 nums 变成 半有序排列 所需的最小操作次数。

排列 是一个长度为 n 的整数序列，其中包含从 1 到 n 的每个数字恰好一次。

示例 1：

输入：nums = [2,1,4,3]
输出：2
解释：可以依次执行下述操作得到半有序排列：
1 - 交换下标 0 和下标 1 对应元素。排列变为 [1,2,4,3] 。
2 - 交换下标 2 和下标 3 对应元素。排列变为 [1,2,3,4] 。
可以证明，要让 nums 成为半有序排列，不存在执行操作少于 2 次的方案。

示例 2：

输入：nums = [2,4,1,3]
输出：3
解释：
可以依次执行下述操作得到半有序排列：
1 - 交换下标 1 和下标 2 对应元素。排列变为 [2,1,4,3] 。
2 - 交换下标 0 和下标 1 对应元素。排列变为 [1,2,4,3] 。
3 - 交换下标 2 和下标 3 对应元素。排列变为 [1,2,3,4] 。
可以证明，要让 nums 成为半有序排列，不存在执行操作少于 3 次的方案。

示例 3：

输入：nums = [1,3,4,2,5]
输出：0
解释：这个排列已经是一个半有序排列，无需执行任何操作。

提示：

2 <= nums.length == n <= 50
1 <= nums[i] <= 50
nums 是一个 排列

解题思路

难度：简单。

思路：最直观的想法是，假设1的下标为p，n的下标为q，那么就分为两种情况。第一种是p<q，那么p移动到0，q移动到n-1，总共(p-0)+(n-1-q)；第二种是p>q，那么p和q交换，一共2*(p-q)-1，p再移动到0，q再移动到n-1，相当于原本的p移动到n-1和q移动到0，一共(n-1-p)+(q-0)+2*(p-q)-1。

int semiOrderedPermutation(vector<int>& nums) 
{
   int n=nums.size();
   //已经是一个半有序排列
   if(nums[0]==1&&nums[n-1]==n)
     return 0;
   int imin,imax;
   int res=0;
   for(int i=0;i<n;i++)
   {
      if(nums[i]==1)
        imin=i;
      else if(nums[i]==n)
        imax=i;
   }
   if(imax>imin)
     res=(n-1-imax)+(imin-0);
   else //中间是排列数
     res=(n-1-imin)+(imax-0)+2*(imin-imax)-1;
   return res;
}

总结：当时临场想到的嘿嘿嘿！！！厉害基拉！！！

2718. 查询后矩阵的和

题目描述

描述：给你一个整数 n 和一个下标从 0 开始的 二维数组 queries ，其中 queries[i] = [typei, indexi, vali] 。

一开始，给你一个下标从 0 开始的 n x n 矩阵，所有元素均为 0 。每一个查询，你需要执行以下操作之一：

如果 typei == 0 ，将第 indexi 行的元素全部修改为 vali ，覆盖任何之前的值。
如果 typei == 1 ，将第 indexi 列的元素全部修改为 vali ，覆盖任何之前的值。
请你执行完所有查询以后，返回矩阵中所有整数的和。

示例 1：

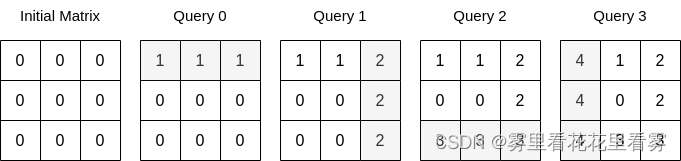
输入：n = 3, queries = [[0,0,1],[1,2,2],[0,2,3],[1,0,4]]
输出：23
解释：上图展示了每个查询以后矩阵的值。所有操作执行完以后，矩阵元素之和为 23 。

示例 2：

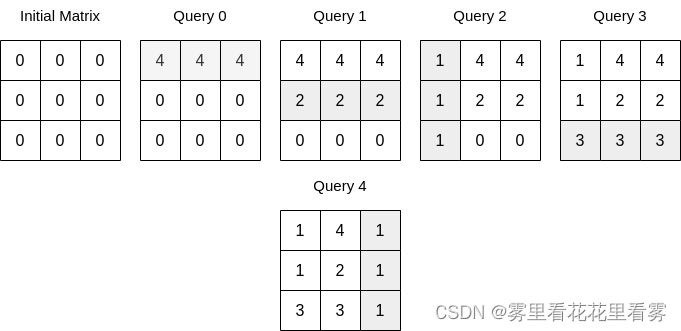
输入：n = 3, queries = [[0,0,4],[0,1,2],[1,0,1],[0,2,3],[1,2,1]]
输出：17
解释：上图展示了每一个查询操作之后的矩阵。所有操作执行完以后，矩阵元素之和为 17 。

提示：

1 <= n <= 104
1 <= queries.length <= 5 * 104
queries[i].length == 3
0 <= typei <= 1
0 <= indexi < n
0 <= vali <= 105

解题思路

2719. 统计整数数目

题目描述

描述：给你两个数字字符串 num1 和 num2 ，以及两个整数 max_sum 和 min_sum 。如果一个整数 x 满足以下条件，我们称它是一个好整数：

num1 <= x <= num2
min_sum <= digit_sum(x) <= max_sum.
请你返回好整数的数目。答案可能很大，请返回答案对 109 + 7 取余后的结果。

注意，digit_sum(x) 表示 x 各位数字之和。

示例 1：

输入：num1 = "1", num2 = "12", min_num = 1, max_num = 8
输出：11
解释：总共有 11 个整数的数位和在 1 到 8 之间，分别是 1,2,3,4,5,6,7,8,10,11 和 12 。所以我们返回 11 。

示例 2：

输入：num1 = "1", num2 = "5", min_num = 1, max_num = 5
输出：5
解释：数位和在 1 到 5 之间的 5 个整数分别为 1,2,3,4 和 5 。所以我们返回 5 。

提示：

1 <= num1 <= num2 <= 1022
1 <= min_sum <= max_sum <= 400

解题思路

难度：难。

思路：最直观的想法是，数位DP模板。

const int MOD=1e9+7;
int f(string s,int min_sum,int max_sum)
{
   int n=s.length();
   //截止每一位的sum
   int memo[n][min(9*n,max_sum)+1];
   memset(memo,-1,sizeof(memo));
   //前导0无影响 012和12和一样
   function<int(int,int,bool)> f=[&](int i,int sum,bool is_limit)->int
   {
      if(sum>max_sum) return 0;
      if(i==n) return sum>=min_sum;
      if(!is_limit&&memo[i][sum]!=-1)
        return memo[i][sum];
      int res=0;
      int up=is_limit?s[i]-'0':9;
      for(int d=0;d<=up;d++)
        res=(res+f(i+1,sum+d,is_limit&&d==up))%MOD;
      if(!is_limit)
        memo[i][sum]=res;
      return res;
    };
    return f(0,0,true);
}
int count(string num1, string num2, int min_sum, int max_sum) 
{
   //计算<=num2的合法数字个数a
   //计算<=num1-1的合法数字个数b
   //那么答案就是a-b
   //考虑到num1是一个字符串 故可直接计算<=num1的合法数字个数 再单独判断num1这个数是否合法
   int ans=f(num2,min_sum,max_sum)-f(num1,min_sum,max_sum)+MOD;  //+MOD避免负数 取模后大小不一定
   int sum=0; 
   for(char c:num1)
     sum+=c-'0';
   ans+=min_sum<=sum&&sum<=max_sum;
   return ans%MOD;
}

总结：数位DP还不太熟练，继续加油~~~