常用模拟低通滤波器的设计——契比雪夫I型滤波器

巴特沃斯滤波器的频率特性曲线在通带和阻带内，幅度特性是单调下降的，如果阶次一定，则在靠近截止 $\Omega_{c}$ 处，幅度下降很多，或者说，为了使通带内衰减足够小，需要的阶次N很高。为了克服这一缺点，采用切比雪夫多项式来逼近所希望的 $\left | H(j\Omega ) \right |^{2}$ 。切比雪夫滤波器的 $\left | H(j\Omega ) \right |^{2}$ 在通带范围内是等幅起伏的，所以在同样的通带内衰减要求下，其阶数比巴特沃斯滤波器要小。

契比雪夫(Chebyshev)滤波器的振幅特性就具有等波纹特性，它有两种形式：

振幅特性在通带内是等波纹的、在阻带内是单调的契比雪夫 I 型滤波器；
振幅特性在阻带内是等波纹的、在通带内是单调的契比雪夫 II 型滤波器；

切比雪夫 I 型滤波器的振幅平方函数为：

$A\left ( \Omega ^{2} \right ) = \left | H_{a} (j\Omega )\right |^{2} = \frac{1}{1+\varepsilon ^{2}*V_{N}\left ( \frac{\Omega }{\Omega _{c}} \right )}$

式中， $\Omega_{c}$ 为有效带通截止频率， $\varepsilon$ 是与通带波纹有关的参量， $\varepsilon$ 大，波纹大， $0< \varepsilon < 1$ ；

$V_{N}$ 为N阶契比雪夫多项式。

$V_{N}(x)= \left\{\begin{matrix} cos(Narccosx) , \left | x \right |\leqslant 1& \\ cosh(Narcoshx), |x|> 1& \end{matrix}\right.$

契比雪夫多项式的递推公式为： $V_{N+1}(x) = V_{x}V_{N}(x) - V_{N-1}(x)$

由此可知，契比雪夫滤波器有 $\Omega_{c}$ 、 $\varepsilon$ 、N 三个参数。

在Matlab 中，函数 cheb1ap、cheb1ord、cheby1 用于设计切比雪夫 I 型滤波器。

1、cheb1ap 函数

在 Matlab 中，函数 cheb1ap 用于设计切比雪夫 I 型低通滤波器，其调用格式为：

[z, p, k] = cheb1ap(n, rp) % 返回契比雪夫 I 型滤波器的零点z、极点p 和增益 k

说明：输入 n 为滤波器的阶数，rp 为通带的幅度误差（滤波器在通带内的最大衰减值），返回的 z 是一个空矩阵。

2、cheb1ord 函数

在 Matlab 中，利用 cheb1ord 函数可以求出所需要的滤波器的阶数和截止频率，滤波器在通带中的损耗不超过 Rp dB，在阻带中的衰减至少为 Rs dB。其调用格式为：

[n, Wn] = cheb1ord(Wp, Ws, Rp, Rs) % 返回值 n 为滤波器的最低阶数，Wn 为截止频率
[n, Wn] = cheb1ord(Wp, Ws, Rp, Rs, 's') % 设计模拟契比雪夫 I 型滤波器的最低阶数n 和截止频率Wn

说明：Wp、Ws、Rp、Rs 分别为通带截止频率、阻带起始频率、通带内波动、阻带内最小衰减。

3、cheby1函数

由切比雪夫 I 型滤波器的阶数 n 以及通带截止频率 Wn 可以计算出对应传递函数 H(z)的分子分母系数。

Matlab 提供 cheby1 函数用于求解契比雪夫 I 型滤波器的系数，函数调用格式为：

[b, a] = cheby1(n, Rp, Wp) % 返回值契比雪夫 I 型低通滤波器传递函数的系数

说明：b 为 H(z)的分子多项式系数，a 为 H(z)的分母多项式系数，Wp 为标准化通带边缘频率，Rp 为峰间通带波纹。

[b, a] = cheby1(n, Rp, Wp, ftype) % 根据 ftype 的值和 Wp 的元素，设计低通、高通、带通或带阻契比雪夫 I 型滤波器，其中带通和带阻设计为 2n 级。
[z, p, k] = cheby1(____) % 设计数字切比雪夫 I 型滤波器，并返回其零点、极点和增益
[A, B, C, D] = cheby1(____) % 设计数字切比雪夫 I 型滤波器，并返回指定其空间状态表示形式的矩阵
[ ____ ] = cheby1(____, 's') % 设计通带边缘角频率为Wp、通带波纹为Rp 的模拟切比雪夫 I 型滤波器

说明：滤波器的传递函数系数：对于低通和高通滤波器，返回长度为 n+1 的行向量；对于带通和带阻滤波器，返回长度为 2n+1 的行向量。

ftype 包括：'low'、'high'、'bandpass' 及 'stop'，含义如下：

'low'：指定通带边缘频率为 Wp 的低通滤波器，为默认值。
'high'：指定通带边缘频率为 Wp 的高通滤波器。
'bandpass' ：指定 2n 阶的带通滤波器，如果 Wp 为两个元素向量，则默认为 'bandpass' 。
'stop'：如果 Wp 为两个元素向量，指定 2n 阶的带阻滤波器。

4、实例演示

【例7-20】设计切比雪夫 I 型低通滤波器示例。

% 【例7-20】设计切比雪夫 I 型低通滤波器示例。
clc, clear, close all

Wp = 3*pi*4*12^3;
Ws = 3*pi*12*10^3;
rp = 1;
rs = 30;
wp = 1; ws = Ws/Wp; % 对参数归一化
[N, wc] = cheb1ord(wp, ws, rp, rs, 's'); % 计算滤波器阶数和阻带起始频率
[z, p, k] = cheb1ap(N, rs); % 计算零点、极点、增益
[b, a] = zp2tf(z, p, k); % 计算系统函数多项式
w = 0:0.02*pi:pi;
[h, w] = freqs(b,a,w); % 模拟滤波器的频率响应
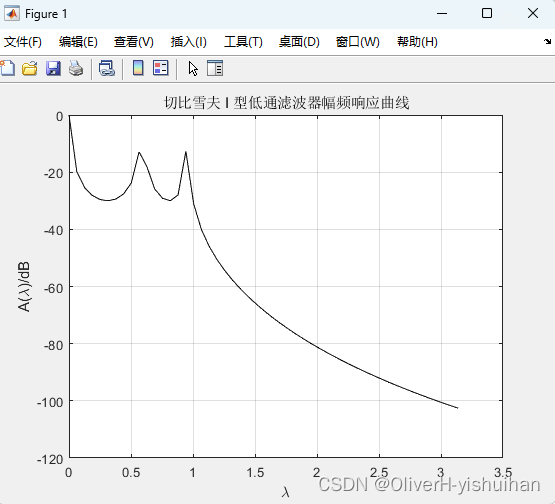
plot(w*wc/wp, 20*log10(abs(h)), 'k');
xlabel('\lambda'); ylabel('A(\lambda)/dB');
title('切比雪夫 I 型低通滤波器幅频响应曲线');  grid on;

【例7-21】设计一个数字高通滤波器，它的通带范围为100~500Hz，通带内允许有0.5dB 的波动，在小于 317Hz 的频带内阻带内衰减至少为 19dB 采样频率为 1000Hz。

% 【例7-21】设计一个数字高通滤波器，它的通带范围为100~500Hz，通带内允许有0.5dB 的波动，
% 在小于 317Hz 的频带内阻带内衰减至少为 19dB 采样频率为 1000Hz。
figure
Wp = [100, 500];
Ws = 317;
rp = 0.5; rs = 19; fs = 1000;
wc = 2*1000*tan(2*pi*400/(2*1000));
wt = 2*1000*tan(2*pi*317/(2*1000));
[N, wn] = cheb1ord(wc, wt, rp, rs, 's'); % 计算滤波器阶数和阻带起始频率
[b, a] = cheby1(N, rp, wn, "high", "s"); % 计算切比雪夫 I 型高通模拟滤波器
[num, den] = bilinear(b, a, fs); % 数字滤波器设计
[h, w] = freqz(num, den); % 数字滤波器的频率响应
f = w/pi*500;
plot(f, 20*log10(abs(h)));
axis([0,500,-80,10]);
xlabel('频率/Hz'); ylabel('幅度/dB');
title('切比雪夫 I 型高通滤波器幅频响应曲线');  grid on;

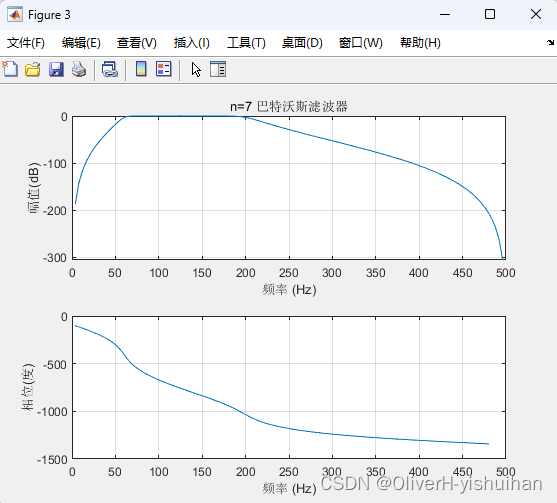
【例7-22】利用cheb1ord 函数示例。它的通带范围为60~200Hz，通带内允许有3dB 的波动，阻带范围为50~250Hz，阻带内衰减至少为 40dB，采样频率为 1000Hz。

% 【例7-22】利用cheb1ord 函数示例。它的通带范围为60~200Hz，通带内允许有3dB 的波动，
% 阻带范围为50~250Hz，阻带内衰减至少为 40dB，采样频率为 1000Hz。
figure
Wp = [60 200]/(1000/2);
Ws = [50 250]/(1000/2); % 对参数进行归一化
Rp = 3; Rs = 40;
[n, Wn] = cheb1ord(Wp,Ws,Rp,Rs); % 计算滤波器最小阶数和截止频率
[b, a] = butter(n,Wn); % 求解巴特沃斯低通滤波器系数
freqz(b,a,128,1000); % 数字滤波器的频率响应
title('n=7 巴特沃斯滤波器');  grid on;