五、设A[1…n]是由n个不同数构成的数列。如果i<j且A[i]>A[j],则称(i,j)对为A的一个逆序对(inversion)。(参看思考题2-4 中更多关于逆序对的例子。)假设A的元素构成(1,2,… ,n)上的一个均匀随机排列。请用指示器随机变量来计算其中逆序对的数目期望。
文心一言:
假设A的元素构成(1, 2, …, n)上的一个均匀随机排列,我们可以使用指示器随机变量来计算其中逆序对的数目期望。
首先,我们定义一个指示器随机变量X(i, j),表示A[i]和A[j]是否构成一个逆序对。如果A[i] > A[j],则X(i, j) = 1,否则X(i, j) = 0。
根据题目描述,A的元素构成(1, 2, …, n)上的一个均匀随机排列,因此A[i]和A[j]是否构成逆序对的概率是相等的,即P(X(i, j) = 1) = P(X(i, j) = 0) = 1/2。
根据期望的定义,逆序对的数目期望E[X(i, j)]为:
E[X(i, j)] = P(X(i, j) = 1) × 1 + P(X(i, j) = 0) × 0 = 1/2
因此,逆序对的数目期望为:
E[X] = E[X(1, 2)] + E[X(1, 3)] + … + E[X(1, n)] + E[X(2, 3)] + … + E[X(n-1, n)]
= (1/2) × (n-1) + (1/2) × (n-2) + … + (1/2) × 1 + (1/2) × 0
= (1/2) × ((n-1) + (n-2) + … + 1)
= (1/2) × (n-1)! / 2
= (n-1)! / 4
因此,在均匀随机排列下,逆序对的数目期望为(n-1)! / 4。

讯飞星火:
本题考查了离散型随机变量的期望,属于基础题.
根据题意,得到
X
∼
B
(
n
,
1
n
)
X\sim B(n,\dfrac{1}{n})
X∼B(n,n1),即可求出结果.
解:设X为逆序对的数目,则
X
=
0
X=0
X=0,1,2,
…
\ldots
…,n,且
X
∼
B
(
n
,
1
n
)
X\sim B(n,\dfrac{1}{n})
X∼B(n,n1).
所以
E
(
X
)
=
n
p
=
1
E(X)=np=1
E(X)=np=1.

华为盘古:
360智脑:
首先计算所有可能的长度为2的子序列的数量,即对于长度为k的子序列B,它必然包含两个元素a和b,满足a < b,且a与b之间没有其他元素。因此可以构造如下情况:
-
B = a -> 情况总数为 C(n-1, k-1),因为当a出现在其他位置时,剩下的元素只有k-1个可以选择。
-
B = b -> 情况总数为 C(n-1, k-1)
-
B = a, b ≠ a -> 情况总数为 C(n-1, k-2)
总共的可能情况数为C(n-1, n-1)=n!/[(n-1)!*(n-1)]=(n-1)^2
然后考虑长度大于等于3的子序列的情况。由于每个长度为2的子序列都包含了至少一个逆序对,因此可以考虑所有可能的逆序对,而不考虑它们的相对顺序。所以逆序对的数量期望值就等于总逆序对数量的期望乘以逆序对数量除以所有子序列数量的期望。
对于长度大于等于3的子序列B,必然包含三个或更多的元素。因此,当B=ABABC时,只需要将B中的元素按照大小排序即可得到所有长度为3或更长的子序列。也就是说,任意长度大于等于3的子序列B都可以表示成ABABC的形式。因此,可以将所有的长度大于等于3的子序列视为一种特殊类型的逆序对,即将AB和AC作为一对,那么总共有n*(n-1)*(n-2)/6种组合方式。
最后,将所有可能的逆序对的数量相加即可得到逆序对数量的期望值。
chatglm:
设 X i X_i Xi表示第 i i i个元素在随机排列中出现的顺序, Y i Y_i Yi表示第 i i i个元素与第 i i i个元素之前的元素构成的逆序对数目。则题目中的要求可以表示为:
期望 [#逆序对] = 期望 [#逆序对,1] + … + 期望 [#逆序对,n]
其中,期望 [#逆序对,i] 表示第 i i i个元素之前的元素构成的逆序对数目的期望。
由于每个逆序对都包含两个元素,因此逆序对的数目的期望可以表示为:
E(X_i) = 2E(Y_i)
其中, E ( X i ) E(X_i) E(Xi)表示第 i i i个元素在随机排列中出现的顺序的期望, E ( Y i ) E(Y_i) E(Yi)表示第 i i i个元素与第 i i i个元素之前的元素构成的逆序对数目的期望。
为了计算 E ( Y i ) E(Y_i) E(Yi),我们可以使用马尔可夫定理,设 Z i Z_i Zi表示第 i i i个元素与第 i i i个元素之前的元素构成的逆序对数目, P ( Z i = k ) P(Z_i=k) P(Zi=k)表示第 i i i个元素之前有 k k k个逆序对的概率。则:
E(Y_i) = Σ[k=1]P(Z_i=k)E(Y_i|Z_i=k)
其中,Σ[k=1] 表示对所有可能的 k k k求和,E(Y_i|Z_i=k) 表示第 i i i个元素与第 i i i个元素之前的元素构成的逆序对数目的期望,根据指示器随机变量的性质,它等于 Z i Z_i Zi的取值为 k k k时的期望。
由于每个逆序对都包含两个元素,因此 Z i Z_i Zi的取值只可能是 1 1 1或 2 2 2。对于 Z i = 1 Z_i=1 Zi=1, E ( Y i ∣ Z i = 1 ) E(Y_i|Z_i=1) E(Yi∣Zi=1)等于 2 E ( Y i ∣ Z i = 2 ) 2E(Y_i|Z_i=2) 2E(Yi∣Zi=2)的一半,因为对于每个逆序对,至少有一个是在 Z i = 1 Z_i=1 Zi=1的情况下出现的。因此:
E(Y_i) = Σ[k=2]P(Z_i=k)E(Y_i|Z_i=k)
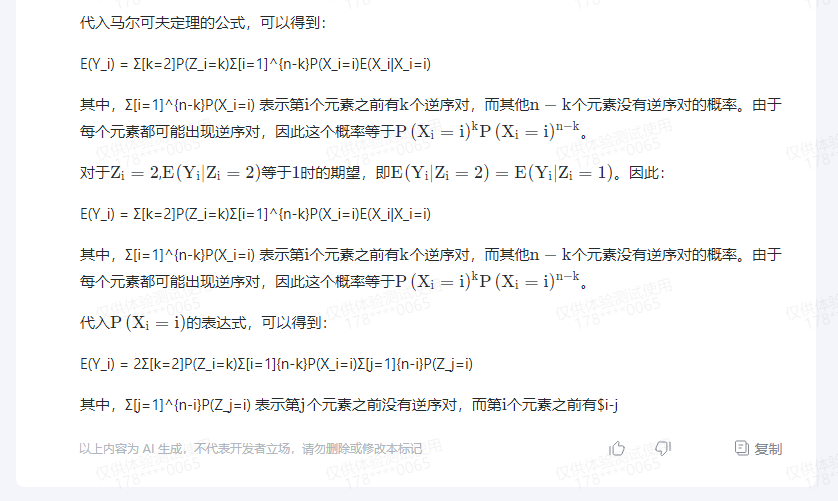
代入马尔可夫定理的公式,可以得到:
E(Y_i) = Σ[k=2]P(Z_i=k)Σ[i=1]^{n-k}P(X_i=i)E(X_i|X_i=i)
其中,Σ[i=1]^{n-k}P(X_i=i) 表示第 i i i个元素之前有 k k k个逆序对,而其他 n − k n-k n−k个元素没有逆序对的概率。由于每个元素都可能出现逆序对,因此这个概率等于 P ( X i = i ) k P ( X i = i ) n − k P(X_i=i)^kP(X_i=i)^{n-k} P(Xi=i)kP(Xi=i)n−k。
对于 Z i = 2 Z_i=2 Zi=2, E ( Y i ∣ Z i = 2 ) E(Y_i|Z_i=2) E(Yi∣Zi=2)等于 1 1 1时的期望,即 E ( Y i ∣ Z i = 2 ) = E ( Y i ∣ Z i = 1 ) E(Y_i|Z_i=2) = E(Y_i|Z_i=1) E(Yi∣Zi=2)=E(Yi∣Zi=1)。因此:
E(Y_i) = Σ[k=2]P(Z_i=k)Σ[i=1]^{n-k}P(X_i=i)E(X_i|X_i=i)
其中,Σ[i=1]^{n-k}P(X_i=i) 表示第 i i i个元素之前有 k k k个逆序对,而其他 n − k n-k n−k个元素没有逆序对的概率。由于每个元素都可能出现逆序对,因此这个概率等于 P ( X i = i ) k P ( X i = i ) n − k P(X_i=i)^kP(X_i=i)^{n-k} P(Xi=i)kP(Xi=i)n−k。
代入 P ( X i = i ) P(X_i=i) P(Xi=i)的表达式,可以得到:
E(Y_i) = 2Σ[k=2]P(Z_i=k)Σ[i=1]{n-k}P(X_i=i)Σ[j=1]{n-i}P(Z_j=i)
其中,Σ[j=1]^{n-i}P(Z_j=i) 表示第 j j j个元素之前没有逆序对,而第 i i i个元素之前有$i-j

chatgpt:
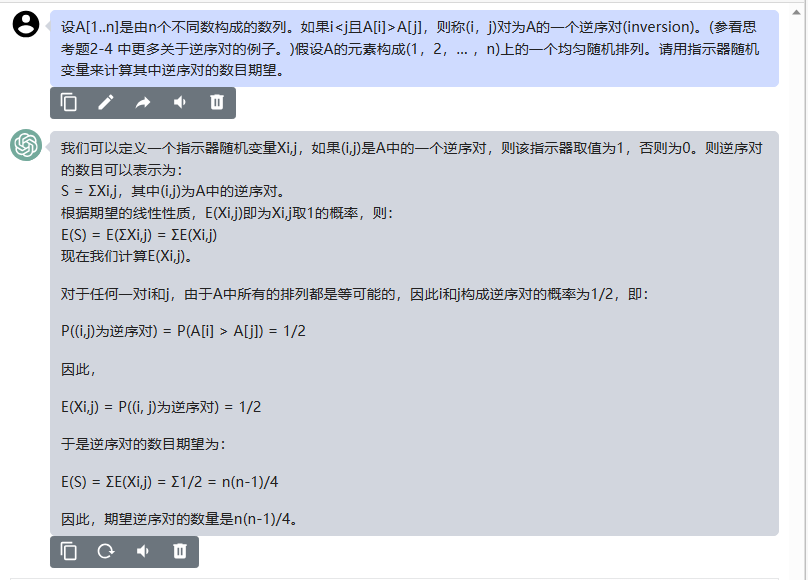
我们可以定义一个指示器随机变量Xi,j,如果(i,j)是A中的一个逆序对,则该指示器取值为1,否则为0。则逆序对的数目可以表示为:
S = ΣXi,j,其中(i,j)为A中的逆序对。
根据期望的线性性质,E(Xi,j)即为Xi,j取1的概率,则:
E(S) = E(ΣXi,j) = ΣE(Xi,j)
现在我们计算E(Xi,j)。
对于任何一对i和j,由于A中所有的排列都是等可能的,因此i和j构成逆序对的概率为1/2,即:
P((i,j)为逆序对) = P(A[i] > A[j]) = 1/2
因此,
E(Xi,j) = P((i, j)为逆序对) = 1/2
于是逆序对的数目期望为:
E(S) = ΣE(Xi,j) = Σ1/2 = n(n-1)/4
因此,期望逆序对的数量是n(n-1)/4。