文章目录
- 概述
- 3.8.1 基本原则
- 3.8.2 指针运算
- 3.8.3 数组与循环
- 3.8.4 嵌套数组
- 3.8.4 固定大小的数组
- 3.8.5 动态分配的数组
概述
C 中数组是一种将标量型数据聚集成更大数据类型的方式。C用来实现数组的方式非常简单,因此很容易翻译成机器代码。C的一个不同寻常的特点是可以对数组中的元素产生指针,并对这些指针进行运算。这些运算会在汇编代码中翻译成地址计算。
优化编译器非常善于简化数组索引所使用的地址计算,弊端是使得 C 代码和它到机器代码的翻译之间的对应关系很难理解。
3.8.1 基本原则
对于数据类型 T T T 和 整常数 N N N,声明:
T A[N];
有两个效果:
首先,它在存储器中分配了 L ∗ N L * N L∗N 字节的连续区域,此处的 L L L 是数据类型 T T T 的大小(单位为字节)。我们用 x A x_A xA 来表示起始位置。
其次,它引入了标识符 A A A, A A A 可以用来作为指向数组开头的指针。这个指针的值就是 x A x_A xA。
可以用 0 ~ N − 1 N-1 N−1 之间的整数索引来访问数组元素。数组元素 i i i 的存放地址为 x A + L ∗ i x_A + L *i xA+L∗i。
举例说明:
char A[12];
char *B[8];
double C[6];
double *D[5];
这些声明会产生带下列参数的数组:

数组
A
A
A 由 12 个单字节(char)元素组成。数组
C
C
C 由 6 个双精度浮点值组成,每个值需要 8 个字节。
B
B
B 和
D
D
D 都是指针数组,因此每个数组元素都是 4 个字节。
IA32 的存储器引用指令被设计用来简化数组访问。例如,假设 E E E 是一个整数数组,而想计算 E [ i ] E[i] E[i],在此, E E E 的地址存放在寄存器 %edx 中,而 i i i 存放在寄存器 %ecx 中。然后,指令
movl (%edx, %ecx, 4), %eax
会执行地址计算 x E + 4 i x_E + 4i xE+4i,在该存储器位置执行读操作,并将结果存放在寄存器 %eax 中。提示:伸缩因子1、2、4、和 8 适用于基本数据类型的大小。
3.8.2 指针运算
C允许对指针进行运算,而计算出来的值会根据该指针引用的数据类型的大小进行调整。即,如果 p p p 是一个指向类型 T T T 的数据的指针, p p p 的值为 x p x_p xp,表达式 p + i p+i p+i 的值为 x p + L ∗ i x_p + L * i xp+L∗i,这里 L L L 是数据类型 T T T 的大小。
单操作数的操作符 & 和 * 可以产生指针和间接引用指针。即,对于一个表示某个对象的表达式Expr,&Expr 表示一个地址。对于表示一个地址的表达式 Addr-Expr,*Addr-Expr 表示该地址中的值。因此,表达式 Expr 与 *&Expr 是等价的。可以对数组和指针应用数组下标操作,如数组引用
A
[
i
]
A[i]
A[i] 与表达式
∗
(
A
+
i
)
*(A+i)
∗(A+i) 是一样的。它计算第
i
i
i 个数组元素的地址,然后访问这个存储器位置。
扩充一下前面的例子,假设整数数组 E 的起始地址和整数索引 i i i 分别存放在寄存器 %edx 和 %ecx 中。下面是一些与 E 有关的表达式以及每个表达式的汇编代码实现,结果存放在寄存器 %eax 中。
| 表达式 | 类型 | 值 | 汇编代码 |
|---|---|---|---|
| E E E | int * | x E x_E xE | movl %edx, %eax |
| E [ 0 E[0 E[0] | int | M [ x E ] M[x_E] M[xE] | movl (%edx), %eax |
| E [ i ] E[i] E[i] | int | M [ x E + 4 i ] M[x_E + 4i] M[xE+4i] | movl (%edx, %ecx, 4), %eax |
| & E [ 2 ] E[2] E[2] | int * | x E + 8 x_E + 8 xE+8 | leal 8(%edx), %eax |
| E + i − 1 E+i-1 E+i−1 | int * | x E + 4 i − 4 x_E+4i-4 xE+4i−4 | leal -4(%edx, %ecx, 4), %eax |
| *(& E [ i ] + i ) E[i] + i) E[i]+i) | int | M [ x E + 4 i + 4 i ] M[x_E + 4i + 4i] M[xE+4i+4i] | movl (%edx, %ecx), %eax |
| & E [ i ] − E E[i] - E E[i]−E | int | i i i | movl %ecx, %eax |
这些例子中,leal 指令用来产生地址,而 movl 用来引用存储器(除了第一种情况是拷贝一个地址)。最后一个例子表明可以计算同一个数组结构中的两个指针之差,结果值是除以数据类型大小后的值。
3.8.3 数组与循环
循环代码内,对数组的引用通常有非常规则的模式,优化编译器会使用这些模式。
例如,下面(a) 中的函数 decimal5,计算的是一个由 5 个十进制数字表示的整数。在把这个函数转换成汇编代码的过程中,编译器产生的代码类似于 b 中的 C 函数 decimal5_opt。
//(a) 原始C代码
int decimal5(int *x)
{
int i;
int val = 0;
for (i = 0; i < 5; i++)
val = (10 * val) + x[i];
return val;
}
//(b) 等价的指针代码
int decimal5_opt(int *x)
{
int val = 0;
int *xend = x + 4;
do {
val = (10 * val) + *x;
x++;
} while (x <= xend);
return val;
}
首先,它不会使用循环变量
i
i
i,而是用指针运算来依次遍历数组元素。它计算出最后一个数组元素的地址,并且把与这个地址的比较作为循环测试。最后,它能使用do-while 循环,因为至少要执行一次循环体。

(c) 中的代码给出了一个进一步的优化,以避免使用整数乘法指令。特别地,它使用 leal(第5行)来计算
5
∗
v
a
l
5 *val
5∗val 作为
v
a
l
+
4
∗
v
a
l
val + 4 *val
val+4∗val。然后,用伸缩因子值为 2 的 leal (第7行)使之扩展为
10
∗
v
a
l
10*val
10∗val。
为什么要避免使用整数乘法?
在较老的 IA32 处理器模型中,整数乘法指令要花费 30 个时钟周期,所以编译器要尽可能地避免使用它。而在大多数新近的处理器模型中,乘法指令只需要 3 个时钟周期,所以不一定会进行这样的优化了。
3.8.4 嵌套数组
即使是创建数组的数组时,数组分配和引用的通用原则也是有效的。
例如,声明
int A[4][3];
等价于声明
typedef int row3_t[3];
row3_t A[4];
数据类型 row3_t 被定义成一个三个整数的数组。数组 A 包含有四个这样的元素,每个都需要 12 个字节来存放三个整数。所以,总的数组大小为 4 * 4 * 3 = 48 字节。
数组 A 还可以看成是一个 4 行 3 列的二维数组,从 A[0][0] 到 A[3][2]。数组元素在存储器中是按照 “行优先” 的顺序排列的,这就意味着先是行 0 的所有元素,后面是行 1 的所有元素,依此类推。
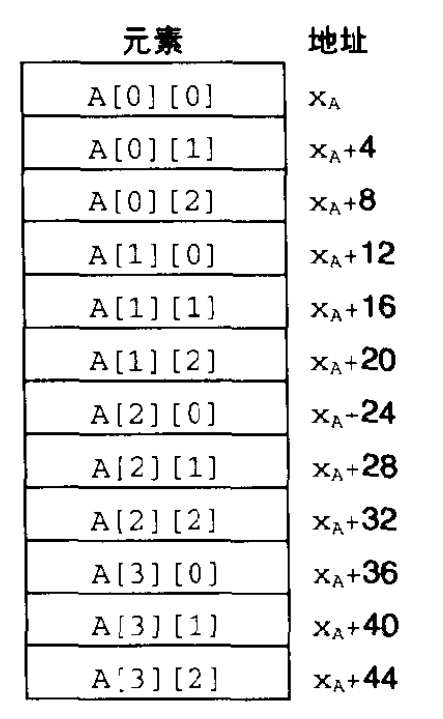
这种排序方法是嵌套声明的结果。将 A 看成一个四元素数组,每个元素又是一个三个 int 的数组,先有 A[0](也就是行0),后面是 A[1],依此类推。
要访问多维数组中的元素,编译器产生的代码要计算待访问元素的偏移,然后再用 movl 指令,以数组的起始作为基地址,偏移(可能需要乘以伸缩因子)作为索引。通常,对一个声明如下的数组:
T D[R][C];
数组元素 D[i][j] 是位于存储器地址 x D + L ( C ∗ i + j ) x_D + L(C *i + j) xD+L(C∗i+j) 的,这里 L L L 是用字节表示的数据类型 T T T 的大小。
如下例子,考虑前面定义的 4 × 3 4 \times 3 4×3 的整数数组。假设寄存器 %eax 包含 x A x_A xA,%edx 保存着 i i i,而 %ecx 保存着 j j j。然后,下面的代码将拷贝数组元素 A [ i ] [ j ] A[i][j] A[i][j] 到寄存器 %eax:
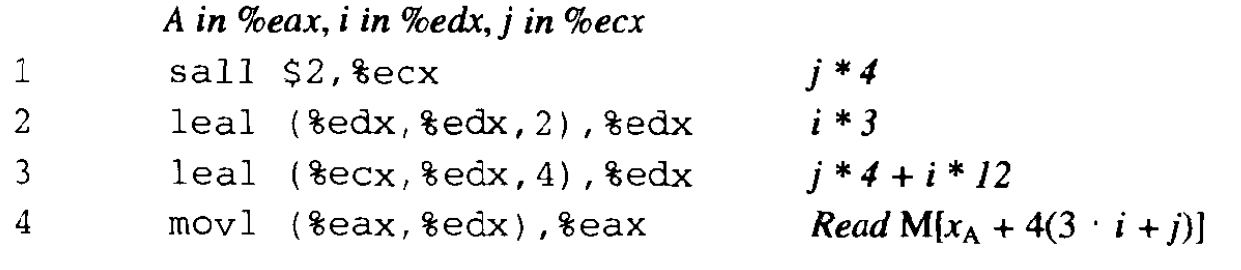
3.8.4 固定大小的数组
对固定大小的多维数组进行操作的代码,C编译器能够进行多种优化。
例如,假设将数据类型 fix_matrix 声明为
16
×
16
16 \times 16
16×16 的整数数组:
#define N 16
typedef int fix_matrix[N][N];
如下的 (a) 中的代码计算矩阵 A 和 B 的乘积的元素 i i i 、 k k k。C编译器产生的代码类似于 (b)中所示的那样,这段代码包含很多聪明的优化。
//(a) 原始的C代码
#define N 16
typedef int fix_matrix[N][N];
/* Compute i,k of fixed matrix product */
int fix_prod_ele(fix_matrix A, fix_matrix B, int i, int k)
{
int j;
int result = 0;
for (j = 0; j < N; j++)
result += A[i][j] * B[j][k];
return result;
}
//(b) 优化过的C代码
/* Compute i,k of fixed matrix product */
int fix_prod_ele_opt(fix_matrix A, fix_matrix B, int i, int k)
{
int *Aptr = &A[i][0];
int *Bptr = &B[0][k];
int cnt = N - 1;
int result = 0;
do {
result += (*Aptr) * (*Bptr);
Aptr += 1;
Bptr += N;
cnt--;
} while (cnt >= 0)
return result;
}
编译器认出循环会依次访问数组 A 的元素 A[i][0],A[i][1],…,A[i][15]。这些元素占据的是存储器中从数组元素 A[i][0] 的地址开始的相邻的位置。因此,程序可以用指针变量 Aptr 来访问这些连续的位置。
循环会依次访问数组B 的元素 B[0][k],B[1][k],…,B[15][k]。这些元素占据的是存储器中从数组元素 B[0][k] 的地址开始的位置,分别相距 64 个字节。因此,程序可以用指针变量 Bptr 来访问这些连续的位置。在 C 中,这个指针会增加 16,尽管实际上真实的指针会增加 4 * 16 = 64。最后,代码可以用一个简单的计数器来记录循环的次数。
给出了 fix_prod_ele_opt 的 C 代码,来说明 C 编译器产生汇编时所使用的优化。如下是这个循环的实际的汇编代码:

注意,上面的汇编代码中,所有的指针增加量均乘以伸缩因子值4。
3.8.5 动态分配的数组
C只支持大小在编译时就能知道的多维数组(第一维可能有些例外)。在许多应用程序中,需要代码能够对动态分配的任意大小的数组进行操作。为此,必须显式地写出从多维数组到一维数组的映射。可以将数据类型 var_matrix 简单地定义为 int *:
typedef int *var_matrix;
用 Unix 的库函数 calloc 来为一个
n
×
n
n \times n
n×n 的整数数组分配和初始化存储:
var_matrix new_var_matrix(int n)
{
return (var_matrix)calloc(sizeof(int), n * n);
}
calloc 函数有两个参数:每个数组元素的大小和所需数组元素的数目。它试着为整个数组分配空间。如果成功,会将整个存储器区域初始化为0,并返回指向第一个字节的指针。如果没有足够的可用空间,它就返回空(null)。
C、C++ 和 Java 中的动态存储器分配和释放
在 C 中,堆(一个可以用来存放数据结构的存储器池)中的存储分配是用的库函数 malloc 或 calloc。它们的效果类似于 C++ 和 Java 中的 new 操作。C 和 C++ 都要求程序显式地用 free 函数来释放已分配的空间。在 Java 中,释放是由运行时系统通过一个称为 garbage collection(垃圾回收)的进程自动完成的。
然后,用行优先顺序的数组下标计算方法确定矩阵元素 i i i、 j j j 的位置 i ∗ n + j i * n + j i∗n+j:
int var_ele(var_matrix A, int i, int j, int n)
{
return A[(i * n) + j];
}
翻译成汇编代码是这样的:

这段代码与用来计算固定大小数组的下标的代码相比,看到动态版本更加复杂。它必须用一条乘法指令来将 i i i 增大 n n n 倍,而不是用一组移位和加法指令。在现代处理器中,这种乘法并不会带来严重的性能损失。
在许多情况中,编译器可以使用相同于已描述的固定大小数组的优化原则,来简化大小可变数组的下标计算。
如下(a) 给出的 C 代码,计算的是两个大小可变矩阵 A 和 B 的乘积的元素 i i i、 k k k。
在(b) 中,给出了一个优化过的版本,它是根据编译原始版本产生的汇编代码逆向生成的。编译器可以利用由循环结构产生的顺序访问模式,消除整数乘法 i ∗ n i * n i∗n 和 j ∗ n j * n j∗n。在这种情况中,编译器不会产生指针变量Bptr,而是创建一个称为 nTjPk(表示 “ n n n 乘以 j j j 加上 k k k”)的整数变量,因为相对于原始代码,它的值等于 n ∗ j + k n * j + k n∗j+k。最开始时, n T j P k nTjPk nTjPk 等于 k k k,每次循环时都增加 n n n。
//(a)原始C代码
typedef int *var_matrix;
/* Compute i,k of variable matrix product */
int var_prod_ele(var_matrix A, var_matrix B, int i, int k, int n)
{
int j;
int result = 0;
for (j = 0; j < n; j++)
result += A[i * n + j] * B[j * n + k];
return result;
}
//(b)优化过的C代码
/* Compute i,k of variable matrix product */
int var_prod_ele_opt(var_matrix A, var_matrix B, int i, int k, int n)
{
int *Aptr = &A[i * n];
int nTjPk = n;
int cnt = n;
int result = 0;
if (n <= 0)
return result;
do {
result += (*Aptr) * B[nTjPk];
Aptr += 1;
nTjPk += n;
cnt--;
} while (cnt):
return result;
}
编译器为循环产生代码,其中寄存器 %edx 保存 cnt,%ebx 保存 Aptr,%ecx 保存 nTjPk,而 %esi
保存结果。这段代码如下:

注意,每次循环时,变量 B 和 n n n 都必须从存储器中读出。这是一个寄存器溢出(register spilling) 的例子。没有足够的寄存器来保存所有需要的临时数据,因此编译器必须将某些局部变量放在存储器中。此时,编译器会选择溢出变量 B 和 n n n ,因为它们只用读一次——在循环里,它们的值不变。寄存器溢出是 IA32 一个很常见的问题,因为处理器的寄存器数量太少了。