设有2个红球,4个白球,先将它们分放到甲、乙两个盒子中去,各方3个。设X为甲盒中的红球数,然后再在甲、乙两盒各取一个进行交换。设Y为此时甲盒中的红球数。
- 求X的分布律。
- 已知X的条件下求Y的分布律。
- 求Y的分布律。

概率空间(Ω,F,P)
随机试验
如果一个试验E满足下列条件:
- 在相同的条件下可以重复进行;
- 每次试验的结果不止一个,并且能事先明确知道试验的所有结果;
- 一次试验结束之前,不能确定哪一个结果会出现。
称此试验为随机试验。
样本空间、随机事件体
随机试验E的每一个最简单的实验结果,称为样本点,记为w。全体样本点构成的集合,称为样本空间,记为Ω。

全概率公式和贝叶斯公式
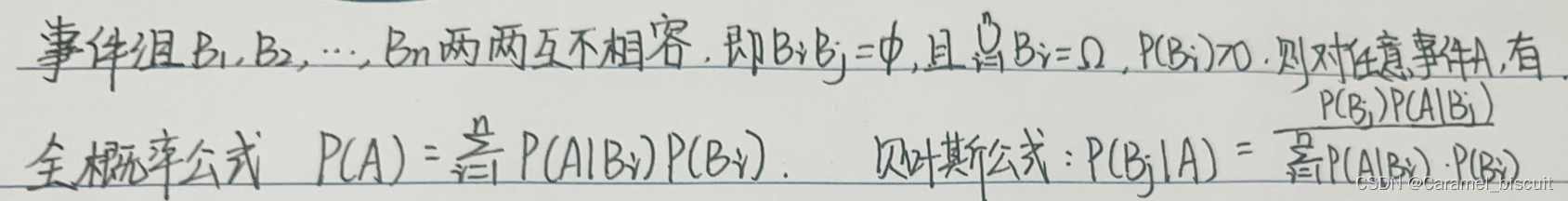
独立过程
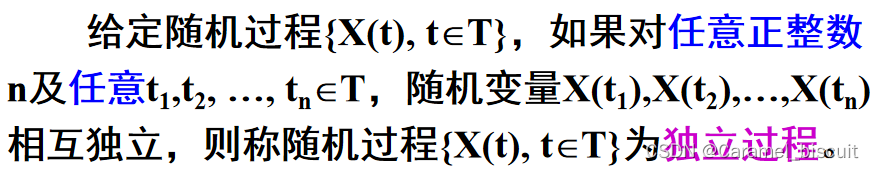
独立增量过程

泊松过程
泊松过程的实例很多,例如:在[0,t)时间内:
- 到达某超级市场的顾客数N(t)
- 某电话交换台的呼唤数N(t)
- 某车间发生故障的机器数N(t)
- 某计数器接受到的粒子数N(t)
- 某信息系统出现的误码数N(t)
马尔可夫过程
当过在t = t0时刻所处的状态已知的情况下,过程在时刻t所处的状态与过程在t = t0时刻之前的状态无关。这种已知“现在”的条件下,将来与过去无关的性质,就是直观意义下的马尔科夫性或称无后效性。具有无后效性的过程称为马尔可夫过程。
独立过程是马尔可夫过程
独立增量过程是马尔可夫过程
状态空间E和参数集T都是离散的马尔可夫过程称为离散参数马氏链
齐次马氏链
在传送数字0和1的通讯系统中,每一传送数字必须经过若干级。第i级正确传送的概率为pi,X(0)表示进入系统第一级的数字,X(n)离开系统第n级的数字