你好,我是郭震(zhenguo)
前几天我们学习强化学习策略迭代,今天,强化学习第8篇:强化学习值迭代
值迭代是强化学习另一种求解方法,用于找到马尔可夫决策过程(MDP)中的最优值函数。
值迭代
值迭代可以总结为如下几点:
值迭代通过不断迭代更新值函数来逼近最优值函数,从而确定最优策略。
值迭代的关键是在每次迭代中更新值函数。
对于每个状态,通过考虑所有可能的动作和下一个状态,选择能够使值最大化的动作,并计算更新后的值函数。
迭代更新值函数,更新公式也是贝尔曼方程,和策略迭代值函数更新公式一样。
值迭代需要进行多次迭代,直到值函数收敛为止。收敛时,值函数不再发生显著变化。
可以看到:值迭代是比策略迭代更为简单的一种迭代方法。
代码实现
值迭代,求迷宫问题,完整代码。
只使用numpy包
import numpy as np定义迷宫地图,在迷宫地图中,不同的数字代表不同的含义:
0:表示可以通过的空格,即可行走的路径。
-1:表示墙壁或障碍物,表示不能通过的障碍物区域。
1:表示目标位置,即终点位置。
其中,0代表可行走的路径,-1代表障碍物或墙壁,1代表迷宫的终点位置。这些数值用于描述迷宫的不同区域,以帮助算法进行路径搜索和价值计算。如下所示:
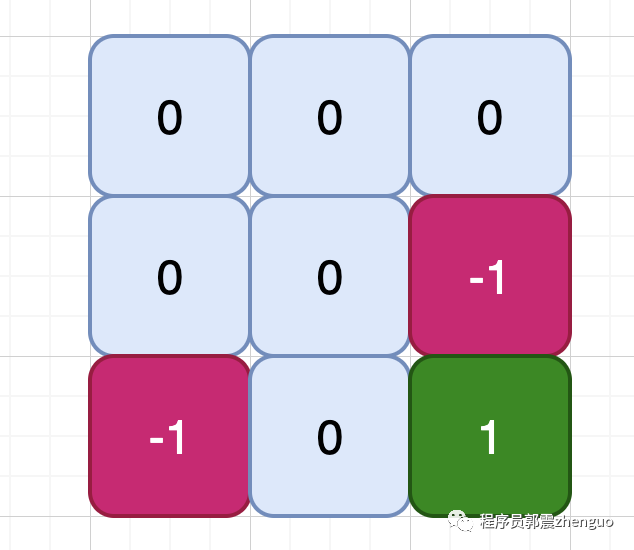
# 定义迷宫地图
maze = np.array([
[0, 0, 0, 0],
[0, -1, 0, -1],
[0, 0, 0, 0],
[-1, 0, -1, 1]
])定义参数
# 定义参数
gamma = 0.9 # 折扣因子
epsilon = 1e-6 # 收敛阈值初始值函数
# 初始化值函数
V = np.zeros(maze.shape)进行值迭代
# 进行值迭代
while True:
delta = 0
for i in range(maze.shape[0]):
for j in range(maze.shape[1]):
if maze[i, j] == -1 or maze[i, j] == 1:
continue
# 计算当前状态的最大价值
max_value = float("-inf")
for action in [(0, 1), (0, -1), (1, 0), (-1, 0)]:
ni, nj = i + action[0], j + action[1]
if ni >= 0 and ni < maze.shape[0] and nj >= 0 and nj < maze.shape[1] and maze[ni, nj] != -1:
max_value = max(max_value, gamma * V[ni, nj])
# 更新值函数
new_value = maze[i, j] + max_value
delta = max(delta, abs(new_value - V[i, j]))
V[i, j] = new_value
if delta < epsilon:
break
# 打印最优值函数
print("最优值函数:")
print(V)这里面的核心代码就是求解贝尔曼方程:
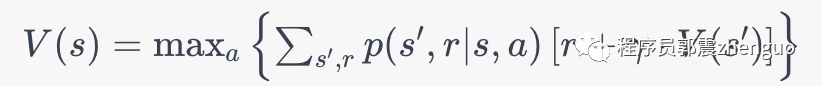
其中, 表示状态 的值函数,即按照某个策略获得的预期回报。 表示选择能够使得值最大化的动作 。 表示对所有可能的下一个状态 和奖励 进行求和。 表示在状态 下执行动作 后转移到状态 且获得奖励 的概率。 是折扣因子,用于平衡当前和未来的奖励。
在上述代码中,首先定义了迷宫地图,并设置了折扣因子和收敛阈值。然后,通过值迭代算法逐步更新值函数,直到值函数的变化小于收敛阈值为止。最后,打印出最优的值函数。
感谢你的点赞和转发,让我更新更有动力