试题A:平方序列
 解题思路:
解题思路:
直接枚举一遍x的取值,然后按照题目给定的式子算出y,每次取x+y的最小值即可
答案为7020
代码实现:
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
#define int long long
const int N=1e4+5;
signed main(){
//记录答案
int res=0x3f3f3f3f;
//循环枚举x
for(int i=2020;i<=N;i++){
//计算y*y;
int t=2*i*i-2019*2019;
//判断该值是否是完全平方数
int j=sqrt(t);
//如果是表示存在y,使得y*y满足题目的等差数列
//每次记录x+y的最小值
if(j*j==t)res=min(j+i,res);
}
cout<<res<<endl;
return 0;
}试题B:质数拆分
 解题思路:
解题思路:
先将1~2019中的所有质数筛选出来,将每个质数视为一个价值为自身值的物品,然后直接利用背包问题求解,即从前i个物品中选,且当前价值为j的所有选法数。
考虑状态转移方程
1.不选当前物品:dp[i][j]+=dp[i-1][j];
2.选当前物品:dp[i][j]+=dp[i-1][j-w[i]];
答案为55965365465060
代码实现:
二维未优化版本
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
#define int long long
const int N=2500;
int prime[N],vis[N],cnt;
//dp[i][j]表示从前i个物品中选且当前值为j的选法数
int dp[N][N];
void init(int n){
for(int i=2;i<=n;i++){
if(!vis[i])prime[++cnt]=i;
for(int j=1;prime[j]*i<=n;j++){
vis[prime[j]*i]=1;
if(i%prime[j]==0)break;
}
}
}
signed main(){
//利用线性筛将1~2019中的质数都筛选出来存储到prime数组中
//由于背包问题下标习惯从1开始,所以prime数组存储的质数下标从1开始
init(2019);
//如果价值为0,则选法只有不选这一种
for(int i=0;i<=cnt;i++)dp[i][0]=1;
for(int i=1;i<=cnt;i++){
for(int j=1;j<=2019;j++){
//不选当前物品
dp[i][j]+=dp[i-1][j];
//选当前物品
if(j>=prime[i])dp[i][j]+=dp[i-1][j-prime[i]];
}
}
cout<<dp[cnt][2019]<<endl;
return 0;
}一维优化版本
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
#define int long long
const int N=2500;
int prime[N],vis[N],cnt;
int dp[N];
void init(int n){
for(int i=2;i<=n;i++){
if(!vis[i])prime[++cnt]=i;
for(int j=1;prime[j]*i<=n;j++){
vis[prime[j]*i]=1;
if(i%prime[j]==0)break;
}
}
}
signed main(){
//利用线性筛将1~2019中的质数都筛选出来存储到prime数组中
//由于背包问题下标习惯从1开始,所以prime数组存储的质数下标从1开始
init(2019);
dp[0]=1;
for(int i=1;i<=cnt;i++){
for(int j=2019;j>=0;j--){
if(j>=prime[i])dp[j]+=dp[j-prime[i]];
}
}
cout<<dp[2019]<<endl;
return 0;
}试题C:拼接
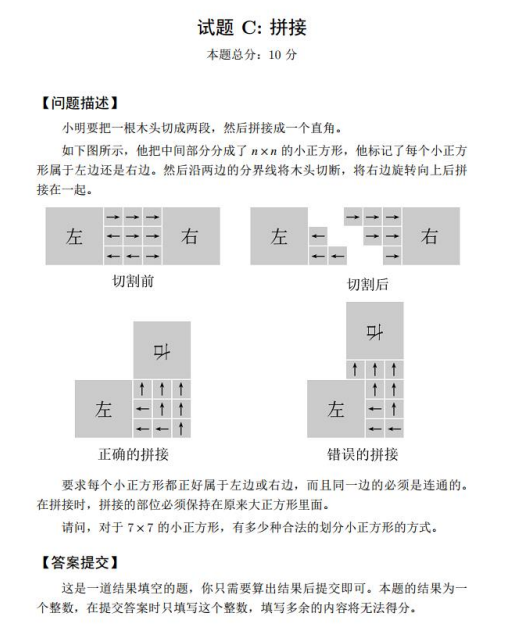 解题思路:
解题思路:
代码实现:
试题D:求值
 解题思路:
解题思路:
直接for循环遍历,每次求当前数的约数个数,如果当前约数个数为100,则输出结果并退出循环
约数个数求法:
答案为45360
代码实现:
#include<iostream>
#include<unordered_map>
using namespace std;
#define int long long
unordered_map<int,int>mp;
void divide(int x){
//从前往后遍历,求解x的质因子及其次幂
for(int i=2;i<=x/i;i++){
//如果当前数能够被x整除,说明i是x的一个因子
//求解i的次幂
while(x%i==0){
x/=i;
mp[i]++;
}
}
//别忘了最后为除尽的数
if(x>1)mp[x]++;
}
signed main(){
//for循环遍历一遍,求每个数的约数个数
for(int i=100;i;i++){
mp.clear();
int res=1;
//分解质因数
divide(i);
//根据公式求解当前数的约数个数
for(auto t:mp)res=res*(t.second+1);
//如果当前数的约数个数为100,则输出当前答案并返回
if(res==100){
cout<<i<<endl;
break;
}
}
return 0;
}试题E:路径计数
 解题思路:
解题思路:
从起点(0,0)开始dfs,dfs每次可以往上、下、左、右四个方向走,每次走过的点都要标记一下,不能重复走,如果步数大于12,则直接return,如果回到了起点(0,0)且当前步数大于2则答案加1
答案为206\(\textcolor{red}{注意步数必须大于2,由于起点是没有被标记的,那么会存在从起点出发立即回到起点的情况,其步数等于2,但是这是不合法的走法}\)
代码实现:
#include<iostream>
#include<unordered_map>
using namespace std;
#define int long long
const int N=10;
int res,vis[N][N];
//模拟上下左右四个方向
int d1[4]={0,0,1,-1};
int d2[4]={1,-1,0,0};
//x,y表示当前所在位置,cnt表示当前的步数
void dfs(int x,int y,int cnt){
//如果步数大于题目要求的12,直接return
if(cnt>12)return;
//如果步数大于2而且当前在起点(0,0),则答案加1并返回
if(cnt>2&&x==0&&y==0){
res++;
return;
}
//往上下左右四个方向递归
for(int i=0;i<4;i++){
int x1=x+d1[i];
int y1=y+d2[i];
//如果被标记了或者越界了,则不能走
if(x1<0||x1>5||y1<0||y1>5||vis[x1][y1])continue;
//标记当前位置被走过了
vis[x1][y1]=1;
//递归,步数加1
dfs(x1,y1,cnt+1);
//恢复现场
vis[x1][y1]=0;
}
}
signed main(){
dfs(0,0,0);
cout<<res<<endl;
return 0;
}试题F:最优包含
 解题思路:
解题思路:
考虑状态转移方程:
dp[i][j]指s1以第i位结尾,s2以第j位结尾的最少修改次数
当s1[i]==s2[j]时,则可以不修改s1,所以dp[i][j]=dp[i-1][j-1]
当s1[i]!=s2[j]时,有两种情况:
1)不修改s1[i],让s1的前i-1个字符与s2前j个字符匹配,此时修改次数不变(因为是包含关系),即dp[i][j]=dp[i-1][j]
2)修改s1[i],让s1的前i-1个字符与s2前j-1个字符相等,此时修改次数加一,即dp[i][j]=dp[i-1][j-1]+1
代码实现:
#include<iostream>
#include<cstring>
using namespace std;
#define int long long
const int N=1005;
//dp[i][j]指s1以第i位结尾,s2以第j位结尾的最少修改次数
int dp[N][N];
signed main(){
//因为求最小值,所以初始化为最大值
memset(dp,0x3f,sizeof dp);
string s1,s2;
cin>>s1>>s2;
//一般dp下标从1开始,所以让字符串前补个空格
s1=" "+s1;
s2=" "+s2;
//边界条件:当s2长度为0时,不需要修改,故为0
for(int i=0;i<=s1.size();i++)dp[i][0]=0;
for(int i=1;i<=s1.size();i++){
for(int j=1;j<=s2.size();j++){
//如果s1[i]==s2[j],则s1的第i位和s2的第j位不需要考虑
//故dp[i][j]=dp[i-1][j-1]
if(s1[i]==s2[j])dp[i][j]=min(dp[i][j],dp[i-1][j-1]);
else{
//如果s1[i]!=s2[j],存在2种情况,可以修改,也可以不修改
//如果修改,则dp[i][j]=d[i-1][j-1]+1;
//如果不修改,则dp[i][j]=dp[i-1][j]
//取二者最小值
dp[i][j]=min(dp[i][j],min(dp[i-1][j-1]+1,dp[i-1][j]));
}
}
}
cout<<dp[s1.size()][s2.size()]<<endl;
return 0;
}试题H:解谜游戏


 解题思路:
解题思路:
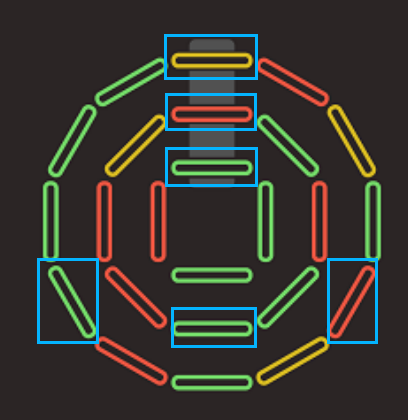
经过观察,每一次旋转只能三个圈一起旋转,但是边长不同,内圈四次一周,中圈八次一周,外圈十二次一周。
设初始时的棒号为内圈0-3,中圈0-7,外圈0-11。
假设内圈的0号棒转动顺时针一周(即整体顺时针转动4次)再次回到0号位置,中圈则是原来的4号棒到了0号位置;外圈则是原来的8号棒到了0号位置。整体再顺时针转动一周的话,内圈的0号位置还是初始时的0号棒,中圈也还是初始的0号棒,外圈则是4号棒;
上述依次类推,会发现内圈的每一根棒无论整体怎么转动都是跟着中圈的两根棒和外圈的三根棒的。
即内圈每一根棒都是跟中圈的两根还有外圈的三根是绑定的。
最后我们可以判断对于这些下标组成的点,绿=3?红=2?黄=1?若满足,我们可以在有限次旋转和交换操作中使得绿色全部移动到外圈,红色全部移动到中圈,黄色移动到内圈
代码实现:
#include<iostream>
#include<unordered_map>
using namespace std;
#define int long long
unordered_map<char,int>mp;
signed main(){
int t;
cin>>t;
while(t--){
string s1,s2,s3;
cin>>s1>>s2>>s3;
int flag=1;
for(int i=0;i<4;i++){
mp.clear();
//外圈
mp[s1[i]]++;
mp[s1[i+4]]++;
mp[s1[i+8]]++;
//中圈
mp[s2[i]]++;
mp[s2[i+4]]++;
//内圈
mp[s3[i]]++;
if(mp['G']!=3||mp['R']!=2||mp['Y']!=1){
flag=0;
break;
}
}
if(flag)cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
return 0;
}