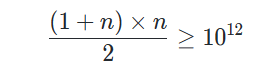试题A:带宽
 解题思路:
解题思路:
由于小蓝家的网络带宽是200Mbps,即200Mb/s,所以一秒钟可以下载200Mb的内容,根据1B=8b的换算规则,所以200Mb=200/8MB=25MB。所以小蓝家的网络理论上每秒钟最多可以从网上下载25MB的内容。
代码实现:
#include<iostream>
#include<algorithm>
using namespace std;
int main(){
cout<<200/8<<endl;
return 0;
}试题B:纯质数
 解题思路:
解题思路:
由于题目要求的是本身是质数而且其所有十进制数位都是质数的数的个数,于是直接先用线性筛对1~20210605的数字进行质数筛选,筛选后的质数存储在prime数组中,再对prime数组(全是质数)进行遍历,依次判断每个质数的每个数位是否都是质数(mp数组用于快速判断某个数是否为质数),如果是,答案加1,否则直接进行下一个质数的判断。
最终答案为:1903
代码实现:
#include<iostream>
#include<algorithm>
#include<unordered_map>
using namespace std;
#define int long long
const int N=20210610;
//prime数组用于存储1~20210605之间的质数
//vis数组用于在线性筛法中判断一个数是否被标记过,
//如果未被标记过,则表示该数为质数,否则代表该数不是质数
//mp数组用于标记某个数是否为质数,便于快速判断一个数是否为质数
int prime[N],vis[N],mp[N],cnt;
void init(int n){
for(int i=2;i<=n;i++){
//如果该数未被标记过,则该数一定为质数
//存储该质数并标记该数为质数
if(!vis[i])prime[cnt++]=i,mp[i]=1;
//利用质数的倍数来标记合数,被标记的一定不是质数
for(int j=0;prime[j]*i<=n;j++){
vis[prime[j]*i]=1;
if(i%prime[j]==0)break;
}
}
}
signed main(){
init(20210605);
int res=0;
//遍历1~20210605中的所有质数
for(int i=0;i<cnt;i++){
int temp=prime[i],flag=1;
while(temp){
//如果存在某个数位不是质数,直接退出
if(!mp[temp%10]){
flag=0;
break;
}
temp/=10;
}
//如果满足该质数所有位都是质数,则答案加1
if(flag)res++;
}
cout<<res<<endl;
return 0;
}试题C:完全日期
 解题思路:
解题思路:
直接模拟,遍历日,如果日大于当前月份的天数,则日变为1,月份加1,如果月份大于12,则月变为1,年加1。
最终答案为:977\(\textcolor{red}{注意不要忘了判断最后一天即2021-12-31该天是否为完全日期数}\)
代码实现:
#include<iostream>
#include<algorithm>
#include<cmath>
#include<unordered_map>
using namespace std;
#define int long long
//用于初始化闰年和平年每个月的天数
//month[1][1~12]表示闰年的1-12月的天数
//month[0][1~12]表示平年的1-12月的天数
int month[2][13]={0,31,28,31,30,31,30,31,31,30,31,30,31,
0,31,29,31,30,31,30,31,31,30,31,30,31};
//判断闰年
int isrun(int x){
if(x%400==0||(x%4==0&&x%100!=0))return 1;
return 0;
}
signed main(){
int res=0;
//y表示年,m表示月,d表示日
int y=2001,m=1,d=1;
//如果当前不是2021年12月31日就继续遍历
while(y!=2021||m!=12||d!=31){
//num用于计算年月日的各个数字之和
int num=y%10+y/10%10+y/100%10+y/1000%10+m%10+m/10%10+d%10+d/10%10;
//求num的平均数
int temp=sqrt(num);
//如果是完全平方数,则答案加1
if(temp*temp==num)res++;
//日加1
d++;
//如果日大于当前月份的最大值,则日变为1,月加1
if(d>month[isrun(y)][m])d=1,m++;
//如果月大于12,则月变为1,年加1
if(m>12)m=1,y++;
}
//最后别忘记判断2021-12-31
//由于可以手算:2+0+2+1+1+2+3+1=12,不是完全日期,答案不用加1
cout<<res<<endl;
return 0;
}试题D:最小权值
 解题思路:
解题思路:
递推:
设dp[i]表示总结点个数为i的二叉树的最小权值,通过遍历总结点,同时遍历左子树的结点个数,右子树的结点个数为总结点树-左子树结点数-1(根结点数),然后直接套公式,每次取最小值即可。
最终答案为:2653631372\(\textcolor{red}{注意右节点数一定不要忘了减去根节点个数1}\)
代码实现:
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<unordered_map>
using namespace std;
#define int long long
const int N=2500;
//dp[i]表示总结点个数为i的二叉树的最小权值
int dp[N];
signed main(){
//初始化为最大
memset(dp,0x3f,sizeof dp);
//没有结点时,权值为0
dp[0]=0;
//遍历总结点个数
for(int i=1;i<=2021;i++){
//遍历左子树结点个数,左子树结点个数最小可以为0,最大为总结点数-1,因为根结点需要消耗一个结点数
for(int j=0;j<i;j++){
//按照公式计算,取所有情况的最小值
dp[i]=min(1+2*dp[j]+3*dp[i-j-1]+j*j*(i-j-1),dp[i]);
}
}
//输出结点个数为2021的二叉树的最小权值
cout<<dp[2021]<<endl;
return 0;
}试题E:大写
 解题思路:
解题思路:
纯签到题,有手就行
直接遍历一遍,如果是小写字母,则根据大小写字母ASCII值相差32进行转换即可
代码实现:
#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
string s;
cin>>s;
for(int i=0;i<s.size();i++){
if(s[i]>='a'&&s[i]<='z')s[i]=s[i]-32;
cout<<s[i];
}
return 0;
}试题F:123
 解题思路:
解题思路:
数列中的每一个连续的部分可以看作一个小区间。
1 1,2 1,2,3 1,2,3,4 ...每一个小区间都是一个 a1=1,d=1 的等差数列,且区间的长度也能构成等差数列。
由于l,r<=10^12,即
所以最多有 1414214 个小区间构成该数列,满足任意 l,r 都能落在里面。
这意味着虽然我们不能直接查询某一位置的前缀和,但可以通过这些小区间来定位和计算某一位置的前缀和。
- 第 i 个区间的元素个数为 i。
- 定义a[i]表示前i个小区间的元素的个数(1-n的和)。则有:a[i]=a[i-1]+i。
- 定义s[i]表示前i个小区间的和。则有:s[i]=s[i-1]+a[i]。
- 对于数列中任意位置i,一定存在一个最大的j满足a[j]<=i,这表示第i个数落在第j+1区间内。
- 对于数列中任意位置i,当它落在第j+1个区间,它是该区间第k个数,则它在数列中的前缀和为:s[j]+a[k],其中k=i-a[j]。
代码实现:
#include<iostream>
#include<algorithm>
using namespace std;
#define int long long
const int N=1500005;
//a[i]表示前i个组包含的数的总个数
//s[i]表示前i个组的所有的数的总和
int a[N],s[N];
int query(int x){
//利用二分查找一个最大的l,使得a[l](前l组的数的个数)小于等于x
int l=0,r=N;
while(l<r){
int mid=l+r+1>>1;
if(a[mid]<=x)l=mid;
else r=mid-1;
}
//由于1+2+...+i的和就等同于前i组数的总个数,所以1~x-a[l]的和就等同于a[x-a[l]]
//前x项的和等同于前l组的和s[l]加上1~x-a[l]的和a[x-a[l]]
return s[l]+a[x-a[l]];
}
signed main()
{
for(int i=1;i<=N;i++){
//预处理a[i]:前i组的数的个数和
//预处理s[i]:前i组的数的总和
a[i]=a[i-1]+i;
s[i]=s[i-1]+a[i];
}
int t;
cin>>t;
while(t--){
int l,r;
cin>>l>>r;
//利用前缀和求解:l~r的和就等同于前r项的和减去前l-1项的和
cout<<query(r)-query(l-1)<<endl;
}
return 0;
}试题G:异或变换

 解题思路:
解题思路:
通过观察数据范围可以发现,直接完全模拟肯定会超时,但是通过手动模拟发现,经过了一定次数后,字符串会变为最初的字符串,所以,我们只需要找到一次循环所需要的变换次数t,将变换次数模上t,然后再对剩余的变换次数进行模拟就不会超时了
代码实现:
#include<iostream>
#include<algorithm>
using namespace std;
#define int long long
signed main(){
//n表示字符串的长度,t表示变换次数
int n,t;
string s,s1;
cin>>n>>t>>s;
//cnt用于记录变为初始串需要经过的变换次数
int cnt=0;
//s1用于记录初始字符串
s1=s;
while(t--){
//s2用于记录一次变换后的字符串
string s2="";
//第一个字符保持不变
s2+=s[0];
//其余字符等于前一个字符与当前的字符的值的异或
for(int i=1;i<s.size();i++){
if(s1[i]==s1[i-1])s2+="0";
else s2+="1";
}
//变换次数加1
cnt++;
//将s1修改为变换后的字符串
s1=s2;
//如果变换后的字符串和最初的字符串相同,则说明发生了循环
//将变换次数直接%一次循环所需要的变换次数即可大大减少模拟变换的次数
if(s1==s)t%=cnt;
}
//输出最后的变换字符串即可
cout<<s1<<endl;
return 0;
}试题H:二进制问题
 解题思路:
解题思路:
一眼数位dp,题目说求一个区间内满足某种条件的数的个数,而且看一眼数据范围10^18,即差不多可以知道用数位dp解决该题了。
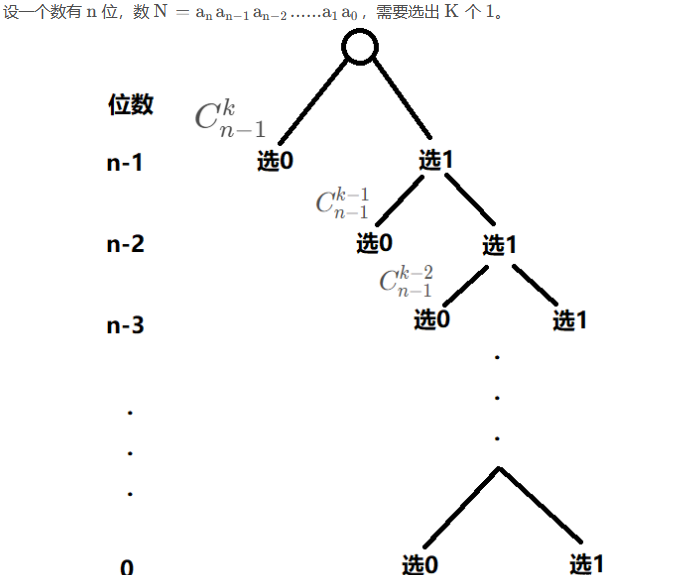
首先分析一下此题的数位dp逻辑
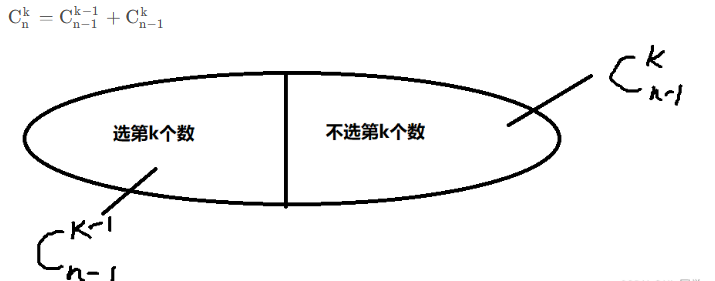
然后预处理一下组合数,组合数求法依旧可以利用dp的思想来求解
代码实现:
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
#define int long long
const int N=65;
int f[N][N];
int r,K;
void init(){
for(int i=0;i<N;i++){
for(int j=0;j<=i;j++){
//组合数定义从前i个数中选,选0个数的选法为1
if(!j)f[i][j]=1;
//否则利用dp递推求解
else f[i][j]=f[i-1][j]+f[i-1][j-1];
}
}
}
int dp(int n){
//如果n为0,那么0中不包含任何1,而题目中K>=1,即1的个数必须>=1,所以0一定不满足条件,返回个数0
if(!n)return 0;
//nums用来存储n的二进制数位(题目要求的是判断二进制的数位中1的个数)
vector<int>nums;
//转换为二进制
while(n)nums.push_back(n%2),n/=2;
//res记录答案,last记录当前已经用了多少个1
int res=0,last=0;
for(int i=nums.size()-1;i>=0;i--){
int x=nums[i];
//如果x>=1才有分析树中的左边分支
if(x>=1){
//res加上左边分支(选0)的选法数
//即从剩下的i位中选K-last个1的选法数
res+=f[i][K-last];
//如果x==1表示存在右分支
if(x==1){
//右分支表示选1,则当前使用的1的个数+1(last++)
last++;
//如果当前选的1的个数>K,说明选多了,直接退出
if(last>K)break;
}
}
//当为最后一位时,如果所消耗1的数量恰好等于规定数量时,即最后一位符合要求
if(!i&&last==K)res++;
}
return res;
}
signed main(){
//预处理组合数
init();
cin>>r>>K;
cout<<dp(r)<<endl;
return 0;
}记忆化搜索方法:
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
#define int long long
const int N=65;
int dp[N][N],a[N];
int x,K;
int dfs(int p,int sum,int limit){
if(!p)return sum==K;
if(!limit&&dp[sum][p]!=-1)return dp[sum][p];
int res=0,up=limit?a[p]:1;
for(int i=0;i<=up;i++){
if(i==1&&K==sum)continue;
res+=dfs(p-1,sum+i,limit&&i==up);
}
if(!limit)dp[sum][p]=res;
return res;
}
int cal(int n){
memset(dp,-1,sizeof dp);
int len=0;
while(n)a[++len]=n%2,n/=2;
return dfs(len,0,1);
}
signed main(){
cin>>x>>K;
cout<<cal(x)<<endl;
return 0;
}试题I:翻转括号序列

 解题思路:
解题思路:
本题正确做法是线段树,但奈何本菜鸡不会线段树,考试也不可能会写线段树,所以就直接暴力解决了,但是没想到蓝桥杯官网里这道题数据比较水,暴力居然能拿满分就离谱
暴力做法:
1.将'('和')'分别对应为1和0
2.修改时,直接暴力枚举,将对应位乘上-1,即可将'('变为')',将')'变为'('
3.查询时,每次加上当前位的值,如果当前值<0说明')'数量超过了'(',则说明已经不是合法的括号序列了,不能继续下去了,直接退出。如果当前值==0,说明'('数量等于')'数量,说明当前位置是一个合法括号序列,记录当前位置,因为要求最长的合法括号序列的右端点位置,则还得继续遍历,直到不满足条件
代码实现:
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e6+5;
int a[N];
int main(){
int n,m;
char c;
cin>>n>>m;
//将'('和')'分别对应为1和0
for(int i=1;i<=n;i++){
cin>>c;
if(c=='(')a[i]=1;
else a[i]=-1;
}
while(m--){
int op;
cin>>op;
if(op==1){
int l,r;
cin>>l>>r;
//直接暴力枚举,将对应位乘上-1,即可将'('变为')',将')'变为'('
for(int i=l;i<=r;i++)a[i]*=-1;
}else{
int l;
cin>>l;
//sum用于记录'('和')'的数量关系
int sum=0,last=0;
for(int i=l;i<=n;i++){
//加上当前值
sum+=a[i];
//当前值<0说明')'数量超过了'(',直接退出
if(sum<0)break;
//当前值==0,说明'('数量等于')'数量,记录位置
if(sum==0)last=i;
}
//输出答案
cout<<last<<endl;
}
}
return 0;
}