目录
1.树的概念及结构
1.1树的概念
1.2.树的表示
1.2.1孩子兄弟表示法
2.2双亲表示法
1.3二叉树在实际中的应用
2.二叉树的概念及结构
2.1二叉树的概念
2.2特殊的二叉树
2.3二叉树的性质
2.4二叉树的实现及其的一些接口(链式)
2.4.1二叉树的实现:
2.4.2前、中、后序遍历
2.4.3求二叉树节点个数
2.4.4求叶子节点个数
2.4.5二叉树的层序遍历
3.哈夫曼树以及哈夫曼编码
1.树的概念及结构
1.1树的概念
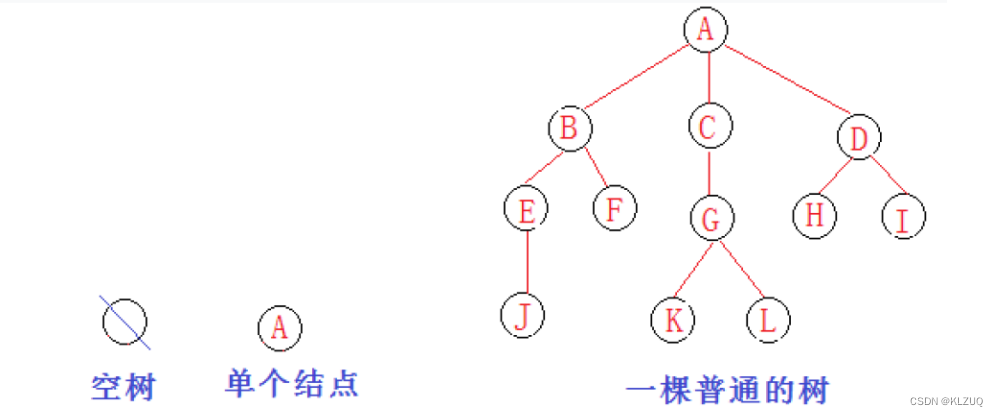
树是一种非线性 的数据结构,它是由 n ( n>=0 )个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。有一个特殊的结点,称为根结点,根节点没有前驱结点除根节点外,其余结点被分成 M(M>0) 个互不相交的集合 T1 、 T2 、 …… 、 Tm ,其中每一个集合 Ti(1<= i <= m) 又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有 0 个或多个后继因此,树是递归定义的。
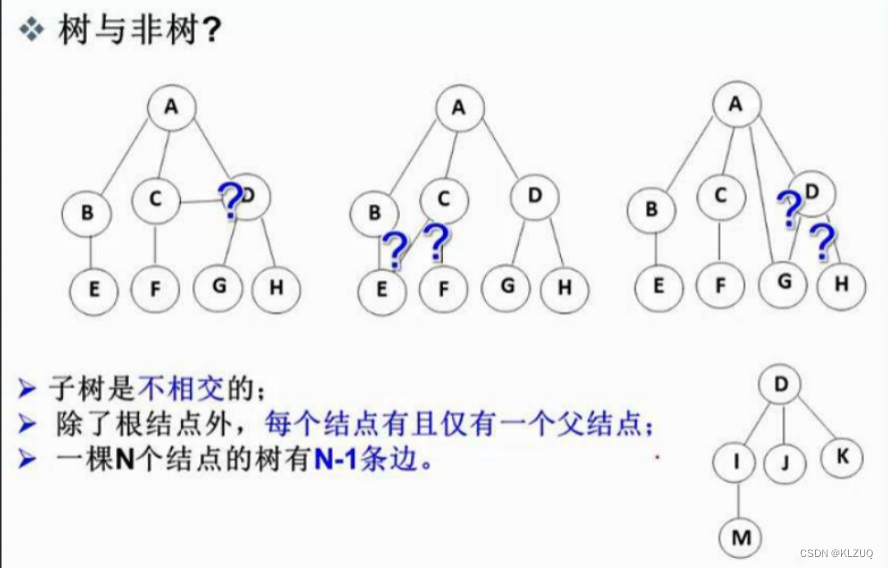
上图中非树的结构叫做图
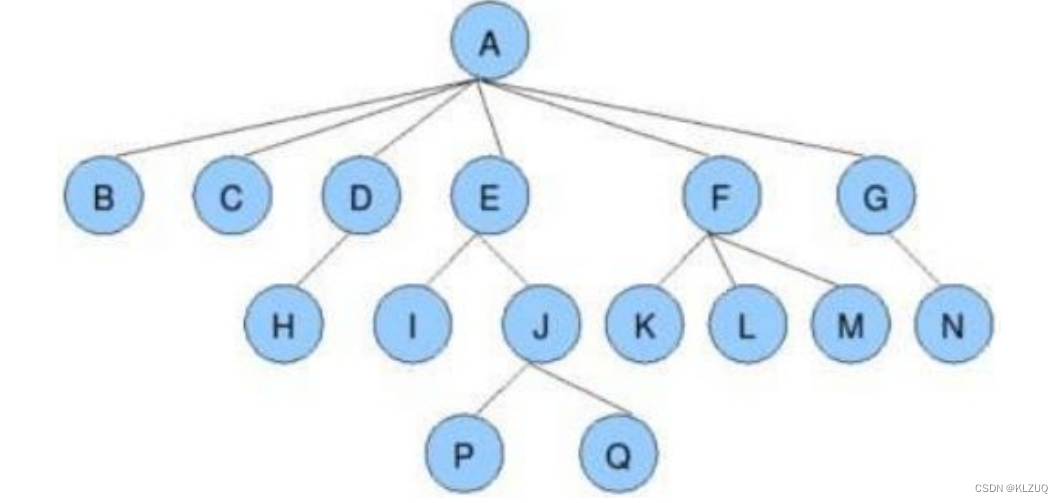
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图: A 的为 6叶节点或终端节点:度为 0 的节点称为叶节点; 如上图: B 、 C 、 H 、 I... 等节点为叶节点非终端节点或分支节点:度不为 0 的节点; 如上图: D 、 E 、 F 、 G... 等节点为分支节点双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图: A 是 B的父节点孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图: B 是 A 的孩子节点兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图: B 、 C 是兄弟节点树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为 6节点的层次:从根开始定义起,根为第 1 层,根的子节点为第 2 层,以此类推;树的高度或深度:树中节点的最大层次; 如上图:树的高度为 4(也有认为从0开始的,但从0开始的话空树就只能用-1表示,所以我们推荐从1开始)节点的祖先:从根到该节点所经分支上的所有节点;如上图: A 是所有节点的祖先子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是 A 的子孙森林:由 m ( m>0 )棵互不相交的多颗树的集合称为森林;(数据结构中的学习并查集本质就是一个森林)
1.2.树的表示
1.2.1孩子兄弟表示法
typedef int DataType;
struct Node
{
struct Node* _firstChild1; // 第一个孩子结点
struct Node* _pNextBrother; // 指向其下一个兄弟结点
DataType _data; // 结点中的数据域
};
这种方法非常巧妙,每个节点都只有一个孩子节点和一个兄弟节点,孩子只保存该节点左边的第一个孩子,剩下的孩子用第一个孩子的兄弟来依次连接,比如上边这棵树a的孩子我们只保存b,而c用b的兄弟去连接,b的孩子我们同样只保存第一个孩子d,剩下的e和f用兄弟节点去连接。
2.2双亲表示法

双亲表示法我们用数组来存储,我们存储的是双亲的下标,比如上边这棵树,我们先储存R,然后存储R的三个孩子A,B,C,我们发现,A,B,C内存储的值为R的下标0,同理,A的孩子D,E也是存储A的下标1,以此类推,我们之后学习的并查集就是使用的双亲表示法
1.3二叉树在实际中的应用

我们实际生活中的文件系统就是用树来表示的。
2.二叉树的概念及结构
2.1二叉树的概念
一棵二叉树是结点的一个有限集合,该集合或者为空,或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。二叉树的特点:1. 每个结点最多有两棵子树,即二叉树不存在度大于 2 的结点。2. 二叉树的子树有左右之分,其子树的次序不能颠倒。
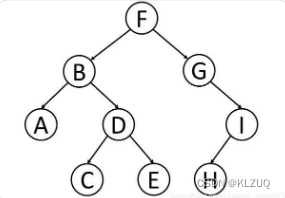
我们可以看到,每个节点最多有两个字节点
任何一棵二叉树,都被分为三个部分
1.根节点
2.左子树
3.右子树
2.2特殊的二叉树
1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为 K ,且结点总数是 (2^k) -1 ,则它就是满二叉树。2. 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K 的,有 n 个结点的二叉树,当且仅当其每一个结点都与深度为 K 的满二叉树中编号从1 至 n 的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。

总的来说,满二叉树就如上图所示,是除了最后一层外所有节点都有两个子节点,完全二叉树是在满二叉树的基础上多了一层,然后从左往右依次连接节点的,是连续的,不能断的
比如以下图片就不属于完全二叉树
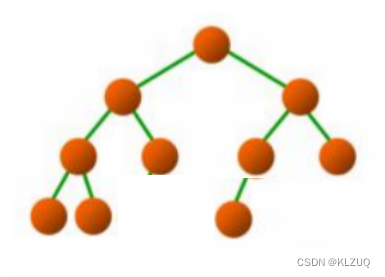

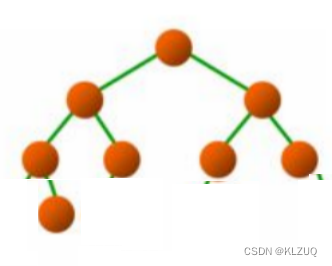
要牢记,最后一层一定是从上一层第一个节点的左节点开始连续
2.3二叉树的性质
1. 若规定根节点的层数为 1 ,则一棵非空二叉树的 第 i 层上最多有 2^(i-1) 个结点 .2. 若规定根节点的层数为 1 ,则 深度为 h 的二叉树的最大结点数是 2^h- 1 .3. 对任何一棵二叉树 , 如果度为 0 其叶结点个数为 n0, 度为 2 的分支结点个数为 n2, 则有 n0 = n2 + 14. 若规定根节点的层数为 1 ,具有 n 个结点的满二叉树的深度 , h=LogN
知道了这些性质,我们来看一道选择题
在具有 2 n 个结点的完全二叉树中,叶子结点个数为( )A nB n + 1C n - 1D n / 2
我们知道,二叉树中有三种节点,度为0,度为1和度为2的节点,叶子节点的度为0,我们设度为0的节点有x0个,度为1的有x1,度为2的有x2,所以我们列出式子:x0+x1+x2=2n
又根据二叉树的性质知:x0=x2+1,所以上面的式子变为:2x0+x1-1=2n
我们又根据完全二叉树的定义知:在完全二叉树里,度为1的节点最多只有一个(最后一层只有一个节点),所以此时我们x1=1
式子变为:2x0+1-1=2n,整理得:x0=n,所以叶子节点有n个,这道题选A
2.4二叉树的实现及其的一些接口(链式)
二叉树可以用顺序存储和链式存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树 会有空间的浪费。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。所以这里我们不写顺序存储。
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的 方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩 子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都 是二叉链。
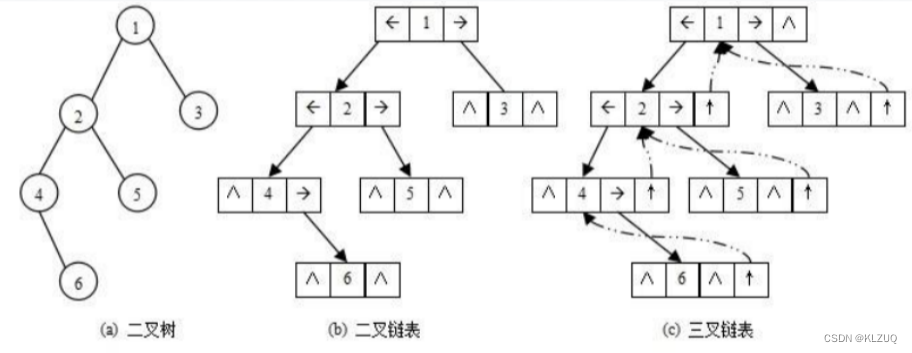
2.4.1二叉树的实现:
typedef char BTDataType;
typedef struct BinaryTreeNode {
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
BTDataType data;
}BTNode;有了二叉树的结构,我们先来实现二叉树的三种遍历
前序 / 中序 / 后序的递归结构遍历 :是根据访问结点操作发生位置命名1. NLR :前序遍历 (Preorder Traversal 亦称先序遍历 )—— 访问根结点的操作发生在遍历其左右子树之前。2. LNR :中序遍历 (Inorder Traversal)—— 访问根结点的操作发生在遍历其左右子树之中(间)。3. LRN :后序遍历 (Postorder Traversal)—— 访问根结点的操作发生在遍历其左右子树之后。
我们选用递归来完成遍历,因为这样写会比较简单一点,但理解起来会难一点
2.4.2前、中、后序遍历
void PrevOrder(BTNode* root)//前序遍历
{
if (root == NULL) {
printf("NULL ");
return;
}
printf("%c ", root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}
void InOrder(BTNode* root)//中序遍历
{
if (root == NULL) {
printf("NULL ");
return;
}
InOrder(root->left);
printf("%c ", root->data);
InOrder(root->right);
}
void PostOrder(BTNode* root)//后序遍历
{
if (root == NULL) {
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%c ", root->data);
}我们用前序遍历,和下图的二叉树来进行举例说明
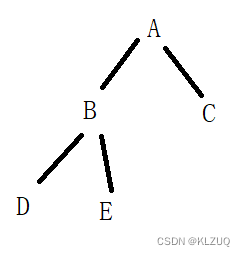
前序遍历的访问顺序为:根 左子树 右子树,在这棵二叉树里,我们的访问顺序为:A,A的左子树,A的右子树,要记住我们前面说的,任何一棵二叉树都会被分为这三部分,所以在前序遍历代码里,我们先打印当前节点数据,在用递归调用访问左子树,任何访问右子树,中途我们会访问到空,比如D,他的左子树和右子树都为空,我们也打印出来,这才是正常的遍历,要记住空也是属于二叉树的一部分,D也是有左右子树的
我们来推一下:首先会打印A,任何访问A的左子树,打印B,任何访问B的左子树,打印D,然后访问D的左右子树,为空,打印两个NULL,此时B的左子树访问完成,然后访问B的右子树,打印E,E的左右子树为空,打印两个NULL,此时B的右子树也访问完成,也就是B访问完成,即A的左子树访问完成,然后访问A的右子树,打印C,同理,C的左右子树为空,打印两个NULL,此时C访问完成,即A的右子树访问完成,遍历完毕,我们来看一下打印结果

和我们想的是一样的,知道了前序遍历,中序和后序也是相同的道理,非常简单
2.4.3求二叉树节点个数
int TreeSize(BTNode* root,int* psize)//求节点个数
{
if(root == NULL){
return 0;
}
else {
++(*psize);
}
TreeSize(root->left, psize);
TreeSize(root->right, psize);
}我们在外部定义size来存储二叉树节点个数,初始为0,然后传size的地址进来即可
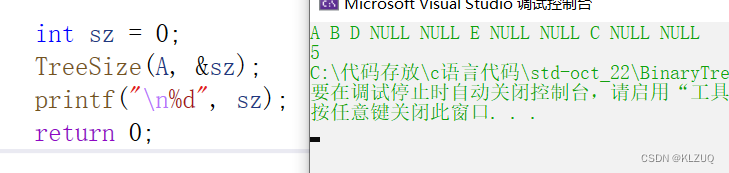
还有更简单的办法
int TreeSize(BTNode* root)//求节点个数
{
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
和遍历一样,采用分治的方法
2.4.4求叶子节点个数
int TreeLeafSize(BTNode* root)//求叶子节点个数
{
if (root == NULL) {
return 0;
}
if (root->left == NULL && root->right == NULL) {
return 1;
}
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}仍是采用分治的方法
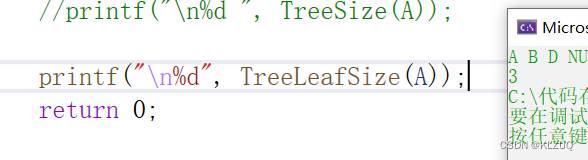
2.4.5二叉树的层序遍历
层序遍历就是一层一层的遍历,比如我们现在的这棵二叉树遍历出来就是ABCDE。
前中后序遍历也叫深度优先遍历,层序遍历是广度优先遍历,层序遍历需要我们使用队列来完成,
这里我把我之前写的队列贴出来
栈和队列及其多种接口实现-c语言_KLZUQ的博客-CSDN博客
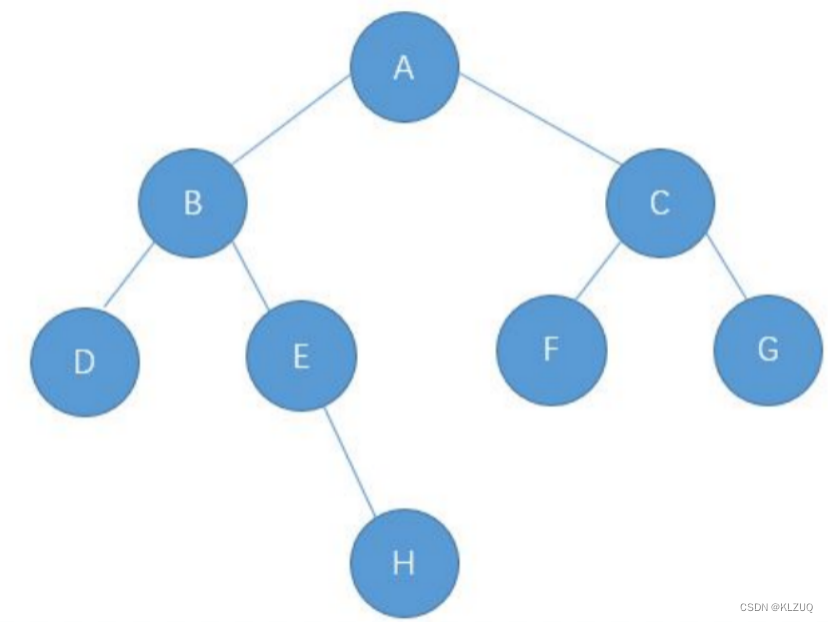
我们来这棵树来给大家举个例子,一会代码输出时仍用我们之前那棵树
层序遍历的思想是上层带下层,我们知道队列的特点是先进先出,我们先把A放入队列,然后A出队列,上层带下层,A出队列时,我们把A的左右子树入队列,即BC入队列,此时队列里的元素为BC,然后B出队列,把B的左右子树入队列,即DE入队列,此时队列里有:CDE,然后C出队列,同时FG入队列,此时队列元素为:DEFG,以此类推。
void Leve10rder(BTNode* root)//层序遍历
{
Queue q;
QueueInit(&q);
if (root != NULL) {
QueuePush(&q, root);
}
while (!QueueEmpty(&q)) {
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%c ", front->data);
if (front->left != NULL) {
QueuePush(&q, front->left);
}
if (front->right != NULL) {
QueuePush(&q, front->right);
}
}
printf("\n");
QueueDestory(&q);
}如果root不为空,入队列,进入循环,队列不为空,取队头元素,然后出队列,同时判断队头元素的左右子树是否为空,若不为空则入队列,最后再销毁队列

这里再补充几个知识,我们得到二叉树的前序和中序遍历结果,就可以还原出二叉树,同样的,得到中序和后续也可以还原出二叉树(要有中序)
我们来看一道选择题
设一课二叉树的中序遍历序列: badce ,后序遍历序列: bdeca ,则二叉树前序遍历序列为 ____ 。A adbceB decabC debacD abcde
我们知道后续遍历为左子树,右子树,根,所以后续遍历的最后一个输出即为二叉树的根节点,我们知道中序遍历为左子树,根,右子树,所以中序遍历里,以a为中心,左边即为左子树,右边为右子树,然后就剩cde了,我们在后续遍历里看到是dec,说明c是a的右子树的根节点,然后根据中序判断出d为左子树,e为右子树,画出树为

根据树我们写出前序遍历为:abcde,选D
3.哈夫曼树以及哈夫曼编码
哈夫曼树及编码非常简单,这里就简单说一下思想及如何完成
哈夫曼树的构建使用贪心算法,会给你几个带权的节点,它是一个从下到上的构建过程,小的在左边,大的在右边
举个例子:a:7,b:5,c:4,d:2,给了我们这四个节点,以及他们对应的权
哈夫曼树会选取其中两个最小的节点构成一个新节点,如上边的c和d,会构成一个权为6的新节点,d在左边,c在右边
同时把这个6再放入上边,和a,b再次进行构建,此时就有三个节点,a:7,b:5以及c和d构成的6,我们再次选取两个最小的,及b和cd构成的新节点,此时b在左边,新节点在右边
同理与a进行构建
树构建好后,会在两边的路上加上数字,左边为0,右边为1,得到以下树
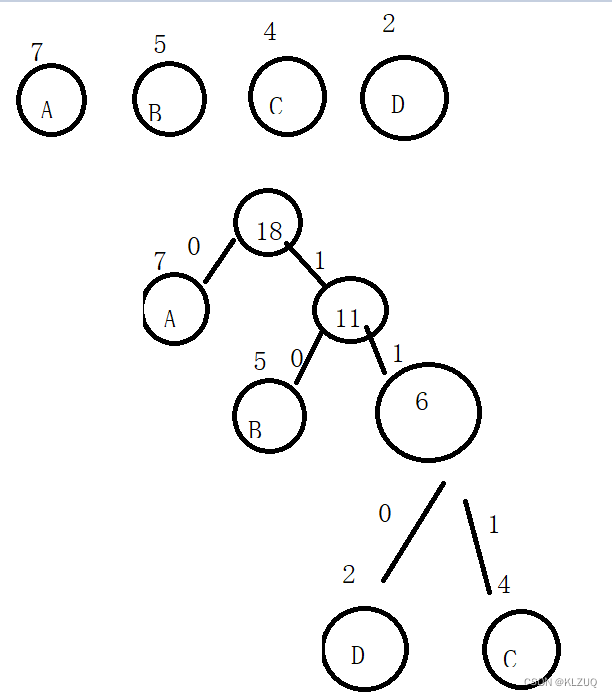
哈夫曼编码就是路径:
a:0
b:10
c:111
d:110
为加权路径最优二叉树,所有原节点 权值*路径长度 和最小,即a*1+b*2+d*3+c*3最小(abcd为对应权值)
权值越大,路径越短,编码越短
权值越小,路径越长,编码越长



![[go学习笔记.第十八章.数据结构] 1.基本介绍,稀疏数组,队列(数组实现),链表](https://img-blog.csdnimg.cn/d7aea688b36e4a96b8e309eccec89c71.png)


![[附源码]Python计算机毕业设计SSM进出口食品安全信息管理系统(程序+LW)](https://img-blog.csdnimg.cn/2e906ab004c946bca34356bdb0ca6d85.png)