在本文中，我们将探讨应用聚类算法（例如k均值和期望最大化）来确定集群的最佳数量时所遇到的问题之一。

最近我们被客户要求撰写关于聚类的研究报告，包括一些图形和统计输出。从数据集本身来看，确定集群数量的最佳值的问题通常不是很清楚。在本文中，我们将介绍几种技术，可用于帮助确定给定数据集的最佳k值。

  【视频】KMEANS均值聚类和层次聚类：R语言分析生活幸福质量系数可视化实例

，时长06:05

 我们将在当前的R Studio环境中下载数据集：

 StudentKnowledgeData <-read_csv（“ YourdownloadFolderPath / StudentKnowledgeData.csv”）

预处理

 由于此数据集的特征向量较低，因此我们将不关注特征选择方面，而是将使用所有可用特征。

 
summary(myDataClean)
[1] 402   5
      STG              SCG              STR              LPR        
 Min.   :0.0000   Min.   :0.0000   Min.   :0.0100   Min.   :0.0000  
 1st Qu.:0.2000   1st Qu.:0.2000   1st Qu.:0.2700   1st Qu.:0.2500  
 Median :0.3025   Median :0.3000   Median :0.4450   Median :0.3300  
 Mean   :0.3540   Mean   :0.3568   Mean   :0.4588   Mean   :0.4324  
 3rd Qu.:0.4800   3rd Qu.:0.5100   3rd Qu.:0.6800   3rd Qu.:0.6500  
 Max.   :0.9900   Max.   :0.9000   Max.   :0.9500   Max.   :0.9900

一旦完成预处理，以确保数据已准备就绪，可用于进一步的应用。

scaled_data = as.matrix（scale（myDataClean））

聚类算法– k表示在其中找到最佳聚类数的示例

让我们尝试为该数据创建聚类。

让我们从k = 3开始并检查结果。

 
kmm
K-means clustering with 3 clusters of sizes 93, 167, 142

Cluster means:
           STG        SCG        STR        LPR        PEG
1  0.573053974  0.3863411  0.2689915  1.3028712  0.1560779
2 -0.315847301 -0.4009366 -0.3931942 -0.1794893 -0.8332218
3 -0.003855777  0.2184978  0.2862481 -0.6421993  0.8776957

Clustering vector:
  1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18  19  20  21 
...................................................................................

Within cluster sum of squares by cluster:
[1] 394.5076 524.4177 497.7787
 (between_SS / total_SS =  29.3 %)

Available components:
[1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
[6] "betweenss"    "size"         "iter"         "ifault"  

当我们检查（between_SS / total_SS）时，发现它很低。该比率实际上说明了群集之间数据点的平方总和。我们想要增加此值，并且随着群集数量的增加，我们看到它增加，但是我们不想过度拟合数据。因此，我们看到在k = 401的情况下，我们将拥有402个完全适合数据的簇。因此，我们的想法是找到一个k值，对于该值，模型不会过拟合，并且同时根据实际分布对数据进行聚类。现在让我们探讨如何解决找到最佳数目的群集的问题。

肘法

如果将集群解释的方差百分比相对于集群数量作图，则第一个集群会添加很多信息（说明很多方差），但在某个点上边际增益会下降，从而在图形。此时选择簇的数量，因此选择“肘部标准”。

 
wss
plot(1:k.max, wss,
     type="b", pch = 19, frame = FALSE, 
     xlab="Number of clusters K",
     ylab="Total within-clusters sum of squares")
 [1] 2005.0000 1635.8573 1416.7041 1253.9959 1115.4657 1026.0506  952.4835  887.7202
 [9]  830.8277  780.2121  735.6714  693.7745  657.0939  631.5901  608.3576

该图可以在下面看到：

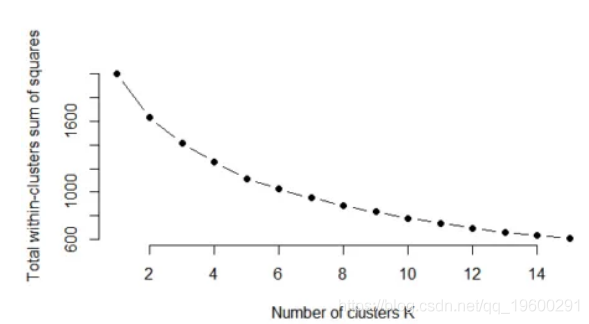
因此，对于k = 4，与其他k相比，between_ss / total_ss比率趋于缓慢变化且变化较小。因此对于该数据，k = 4应该是群集数量的一个不错的选择，

k均值的贝叶斯推断标准

k均值模型“几乎”是高斯混合模型，因此可以构造高斯混合模型的似然性，从而确定信息标准值。
 

 
d_clust$BIC
plot(d_clust)
Bayesian Information Criterion (BIC):
         EII       VII       EEI       VEI       EVI       VVI       EEE       EVE
1  -5735.105 -5735.105 -5759.091 -5759.091 -5759.091 -5759.091 -5758.712 -5758.712
2  -5731.019 -5719.188 -5702.988 -5635.324 -5725.379 -5729.256 -5698.095 -5707.733
3  -5726.577 -5707.840 -5648.033 -5618.274 -5580.305 -5620.816 -5693.977 -5632.555
..................................................................................
         VEE       VVE       EEV       VEV       EVV       VVV
1  -5758.712 -5758.712 -5758.712 -5758.712 -5758.712 -5758.712
2  -5704.051 -5735.383 -5742.110 -5743.216 -5752.709 -5753.597
3  -5682.312 -5642.217 -5736.306 -5703.742 -5717.796 -5760.915
..............................................................

Top 3 models based on the BIC criterion:
    EVI,3     EVI,4     EEI,5 
-5580.305 -5607.980 -5613.077 
> plot(d_clust)
Model-based clustering plots: 

1: BIC
2: classification
3: uncertainty
4: density

Selection: 1

可以在下面看到该图，其中k = 3和k = 4是可用的最佳选择。

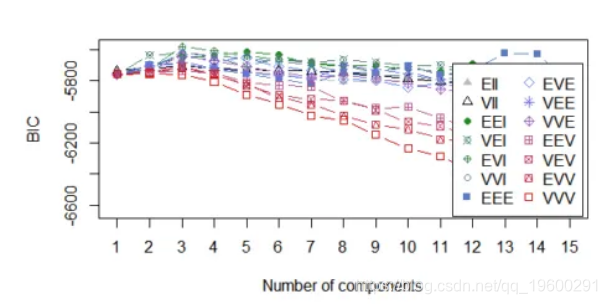
从这两种方法可以看出，我们可以在一定程度上确定对于聚类问题而言，聚类数的最佳值是多少。几乎没有其他技术可以使用。

 
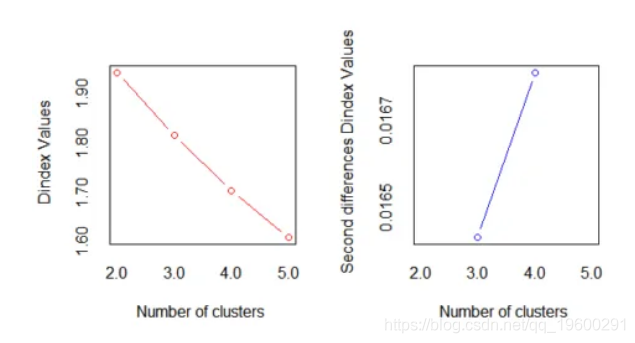
hist(nb$Best.nc[1,], breaks = max(na.omit(nb$Best.nc[1,])))

在此有一个重要的要点，即对于每个群集大小，此方法始终考虑大多数索引。因此，重要的是要了解哪些索引与数据相关，并根据该索引确定最佳选择是建议的最大值还是任何其他值。
正如我们在下面查看“第二差分D-index”图所看到的，很明显，最佳聚类数是k = 4。