12.数据结构之AVL树

news2024/10/5 0:18:43

前言

提到平衡二叉查找树，不得不提二叉查找树。二叉查找树，说简单点，其实就是将我们的数据节点，有序的维护为一个树形结构。这样我们查的时候，那么我们查找某个节点在不在集合中的时间复杂度实际上就是树的高度。如果节点在根节点左右均匀分布，那么维护的树的高度就会最低。

本节，我会详细介绍如何将一个不平衡的二叉树重新平衡。

1. 概念

1.1 平衡二叉树

平衡二叉树(Self-Balancing Binary Search Tree或Height-Balanced Binary SearchTree)，是一种二叉排序树，其中每一个节点的左子树和右子树的高度差至多等于1。也就是说，平衡二叉树要么它是一棵空树，要么它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1。

有两位俄罗斯数学家GMAdelson-Velskii和EMLandis在1962年共同发明一种解决平衡二叉树的算法，所以有不少资料中也称这样的平衡二叉树为AVL树。

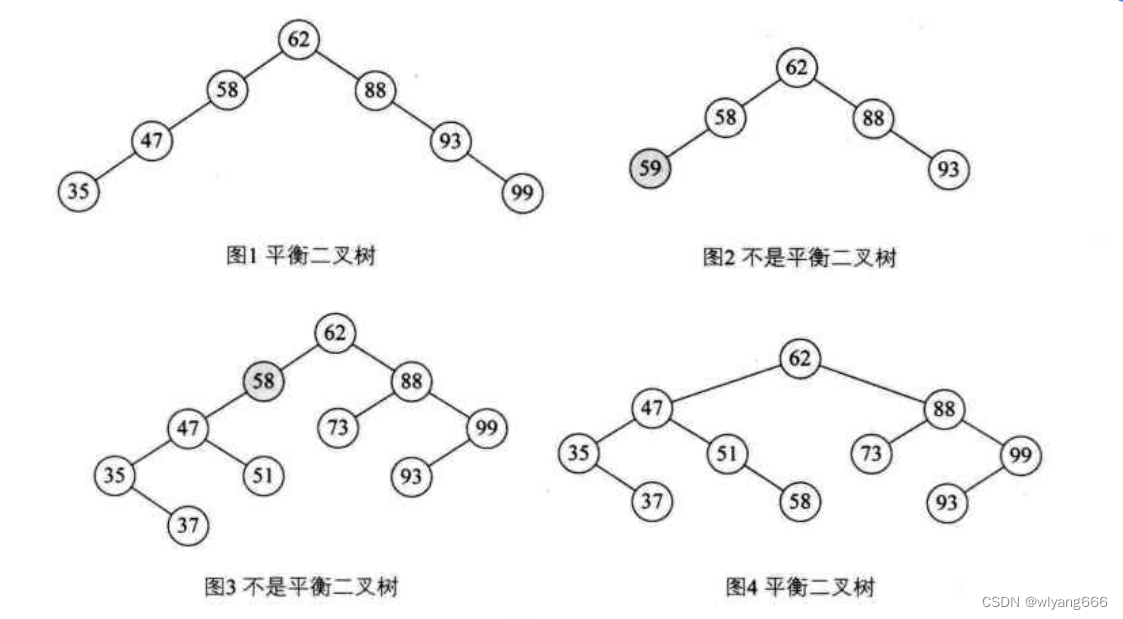
在这里插入图片描述
如上图举例所示：

  1. 图1 是平衡二叉树，因为每个节点左右字树差值都不超过1
  2. 图二不是平衡二叉树，是因为树首先得是二叉排序树，才能是平衡二叉树，但是图二 59 大于 58 ，不应该在58 的左子节点
  3. 图3 不是平衡二叉树，是因为插入37 后，节点58 左子树减去右子树高度为2，不满足条件
  4. 图4 是平衡二叉树

1.2 平衡因子

我们将二叉树上结点的左子树深度减去右子树深度的值称为平衡因子BF(BalanceFactor)，那么平衡叉树上所有结点的平衡因子只可能是-1、0和1，只要二叉树上有一个结点的平衡因子的绝对值大于1，则该二叉树就是不平衡的。

1.3 最小不平衡子树

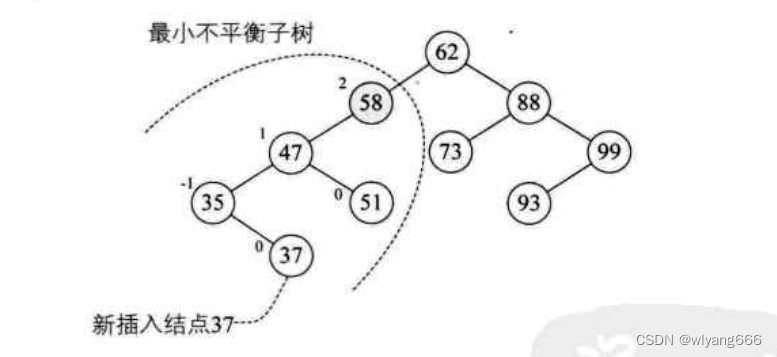
距离插入结点最近的，且平衡因子的绝对值大于1的结点为根的子树，我们称为最小不平衡子树。由此可得，在上面的图3中，最小不平衡子树是58 以下的子树。
在这里插入图片描述

2. 实现原理

平衡二叉树构建的基本思想就是在构建二叉排序树的过程中，每当插入一个结点时，先检查是否因插入而破坏了树的平衡性，若是，则找出最小不平衡子树。在保持二叉排序树特性的前提下，调整最小不平衡子树中各结点之间的链接关系，进行相应的旋转，使之成为新的平衡子树。

我们以数组节点{3，2，1，4，5，6，7，10，9，8}为例，构造平衡二叉树：

  1. 对于数组a[10]={3,2,1,5,710,9,8的前两位3和2我们很正常地构建到了第3个数“1”时，发现此时根结点“3”的平衡因子变成了2，此时整棵树都成了最小不平衡子树，因此需要调整如图1 (结点左上角数字为平衡因子BF值)。因为BF值为正，因此我们将整个树进行右旋(顺时针旋转)，此时结点2成了根结点，3成了2的右孩子，这样三个结点的BF值均为0非常的平衡，如图2所示。
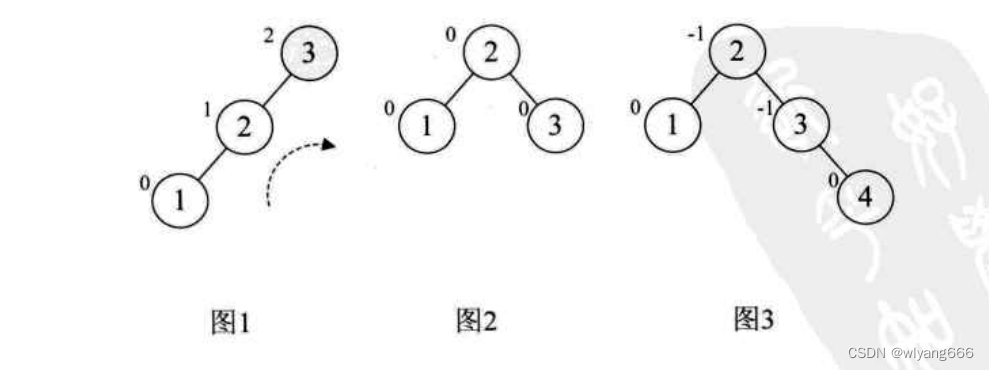
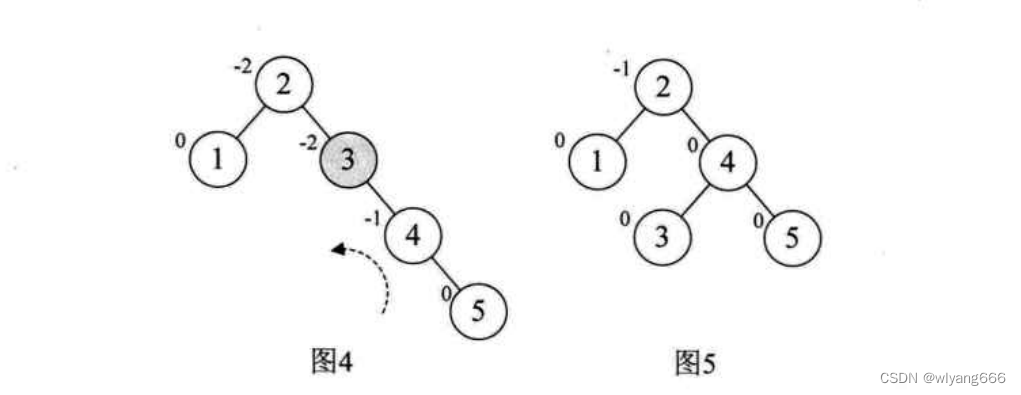
    在这里插入图片描述
  2. 然后我们再增加结点4，平衡因子没发生改变，如图3。增加结点5时，结点3的BF值为-2，说明要旋转了。由于BF是负值，所以我们对这棵最小平衡子树进行左旋(逆时针旋转)，如图4，此时我们整个树又达到了平衡。

在这里插入图片描述

  1. 继续增加结点6时，发现根结点2的BF值变成了-2,。如图6，所以我们对根结点进行了左旋，注意此时本来结点3是4的左孩子，由于旋转后需要满足二叉排序树特性，因此它成了结点2的右孩子，如图7。增加结点7，同样的左旋转，使得整棵树达到平衡，如图8和图9所示。
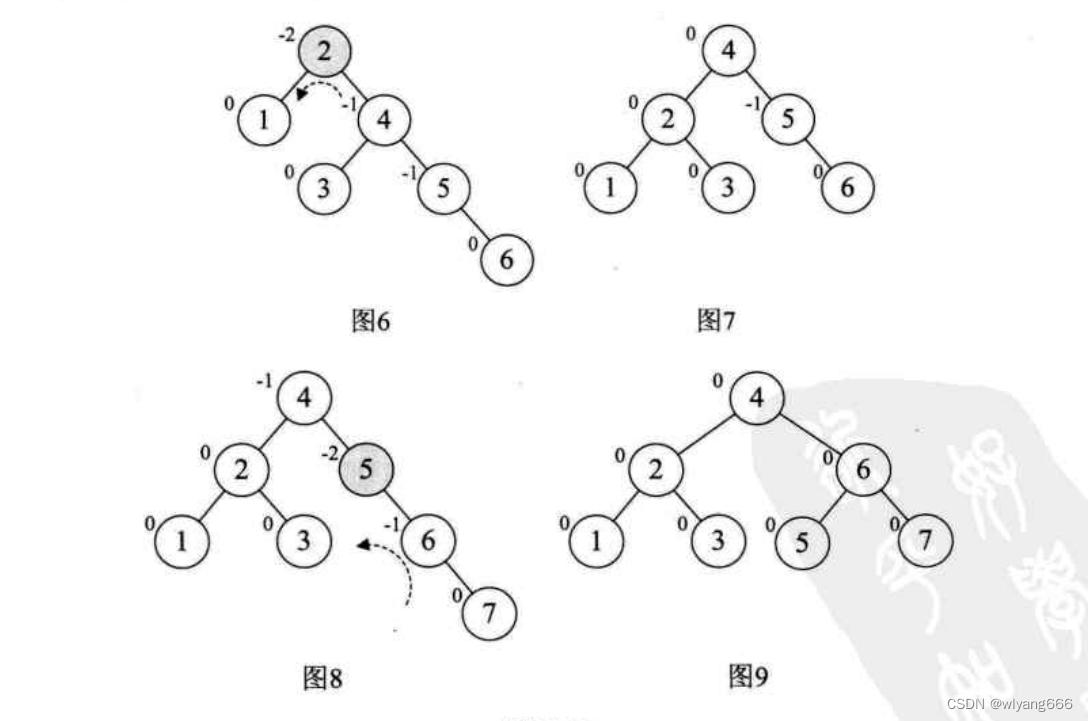
    在这里插入图片描述

  2. 当增加结点10时，结构无变化，如图10。再增加结点9，此时结点7的BF变成了-2，理论上我们只需要旋转最小不平衡子树7，9，10即可，但是如果左旋转后，结点9就成了10的右孩子，这是不符合二叉排序树的特性，此时不能简单的左旋，如图11所示。
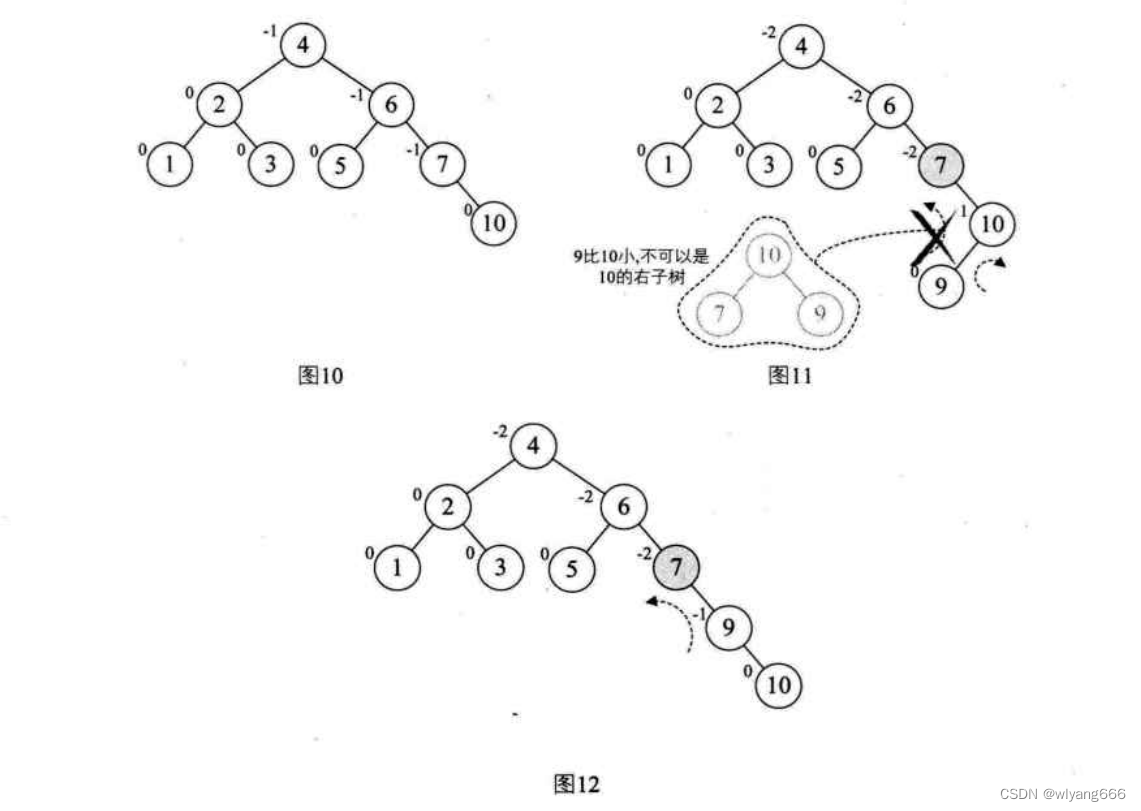
    在这里插入图片描述

  3. 仔细观察图11，发现根本原因在于结点7的BF是-2而结点10的BF是1也就是说，它们俩一正一负，符号并不统一，而前面的几次旋转，无论左还是右旋最小不平衡子树的根结点与它的子结点符号都是相同的。这就是不能直接旋转的关键。那怎么办呢?

    不统一，不统一就把它们先转到符号统一再说，于是我们先对结点9和结点10进行右旋使得结点10成了9的右子树，结点9的BF为-1，此时就与结点7的BF值符号统一了，如图12所示。

  4. 这样我们再以结点7为最小不平衡子树进行左旋，得到图13。接着插入8，情况与刚才类似，结点6的BF是-2，而它的右孩子9的BF是1，如图14，因此首先以9为根结点，进行右旋，得到图15，此时结点6和结点7的符号都是负，再以6为根结点左旋，最终得到最后的平衡二叉树，如图16所示。
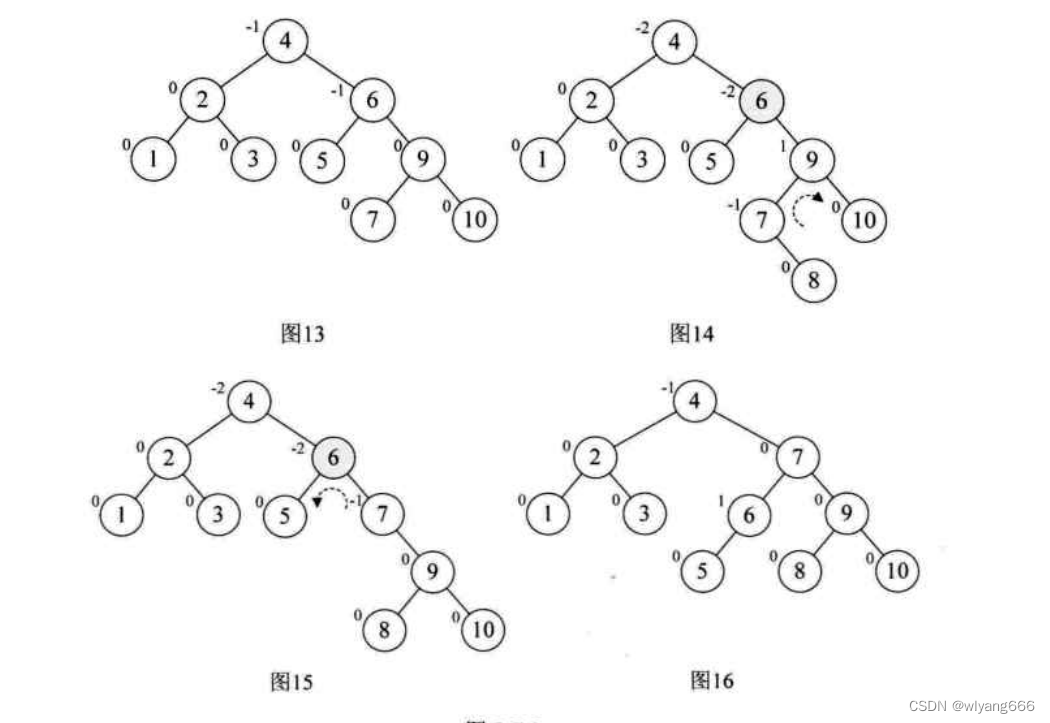
    在这里插入图片描述

通过刚才这个例子，你会发现，所谓的平衡二叉树，其实就是在二叉排序树创建过程中保证它的平衡性，一旦发现有不平衡的情况，马上处理，这样就不会造成不可收拾的情况出现。

当最小不平衡子树根结点的平衡因子BF是大于1时，就右旋，小于-1时就左旋，如上例中结点1、5、6、7的插入等。插入结点后，最小不平衡子树的BF与它的子树的BF符号相反时就需要对结点先进行一次旋转以使得符号相同后，再反向旋转一次才能够完成平衡操作，如上例中结点9、8的插入时。

3. 代码实现

3.1 定义树节点和树类

3.1.1 定义AVL树节点类

package org.wanlong.tree;

/**
 * @author wanlong
 * @version 1.0
 * @description: 平衡二叉树节点
 * @date 2023/6/5 19:03
 */
public class AVLNode<T> {

    //数据
    T data;
    //左孩子
    AVLNode<T> left;
    //右孩子
    AVLNode<T> right;

    //高度
    int height;


    public AVLNode(T data) {
        this.data = data;
    }
}

3.1.2 定义平衡树类

package org.wanlong.tree;

/**
 * @author wanlong
 * @version 1.0
 * @description: 平衡二叉查找树
 * @date 2023/6/1 15:47
 */
public class AVLTree<T extends Comparable<? super T>> {

    //根节点
    private AVLNode<T> root;

    //允许最大的不平衡因子
    private static final int ALLOWED_IMBALANCE = 1;

    //返回树的高度
    private int height(AVLNode<T> t) {
        return t == null ? -1 : t.height;
    }
    public boolean isEmpty() {
        return root == null;
    }

    public void makeEmpty() {
        root = null;
    }

    public T findMin() {
        return findMin(root).data;
    }

    public T findMax() {
        return findMax(root).data;
    }

    /**
     * @param root:
     * @return org.wanlong.tree.AVLNode<T>
     * @Description:找最小节点
     * @Author: wanlong
     * @Date: 2023/6/5 20:00
     **/
    private AVLNode<T> findMin(AVLNode<T> root) {
        if (root == null) {
            return null;
        } else if (root.left == null) {
            return root;
        }
        return findMin(root.left);
    }

    /**
     * @param root:
     * @return org.wanlong.tree.AVLNode<T>
     * @Description:找最大节点
     * @Author: wanlong
     * @Date: 2023/6/5 19:30
     **/
    private AVLNode<T> findMax(AVLNode<T> root) {
        if (root == null) {
            return null;
        } else if (root.right == null) {
            return root;
        } else {
            return findMax(root.right);
        }
    }


    /**
     * @return void
     * @Description: 打印
     * @Author: wanlong
     * @Date: 2023/6/5 19:31
     **/
    public void printTree() {
        if (isEmpty()) {
            System.out.println("节点为空");
        } else {
            printTree(root);
        }
    }

    /**
     * @return void
     * @Description: 打印
     * @Author: wanlong
     * @Date: 2023/6/5 19:31
     **/
    public void printTree(AVLNode<T> root) {
        if (root != null) {
            System.out.print(root.data);
            if (null != root.left) {
                System.out.print("左边节点" + root.left.data);
            }
            if (null != root.right) {
                System.out.print("右边节点" + root.right.data);
            }
            System.out.println();
            printTree(root.left);
            printTree(root.right);
        }
    }
}

3.2 右旋RR

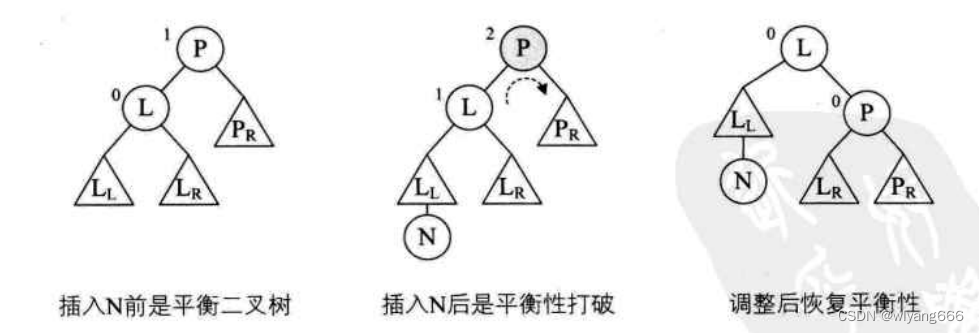
在这里插入图片描述

3.2.1 思路

如图所示。当传入一个二叉排序树P

  1. 将它的左孩子结点定义为L,将L的右子树变成P的左子树
  2. 将P改成L的右子树
  3. 将L替换P成为根结点
  4. 重新计算树的高度
  5. 这样就完成了一次右旋操作，图中三角形代表子树，N代表新增结点。调整完后，需要重新计算树的高度。

3.2.2 代码

/**
 * @param p: 最小不平衡子树
 * @return void
 * @Description:右旋
 * @Author: wanlong
 * @Date: 2023/6/5 18:36
 **/
AVLNode<T> rightRotate(AVLNode p) {
    AVLNode k1 = p.left;
    p.left = k1.right;
    k1.right = p;
    p.height = Math.max(height(p.left), height(p.right)) + 1;
    k1.height = Math.max(height(k1.left), p.height) + 1;
    return k1;
}

3.3 左旋LL

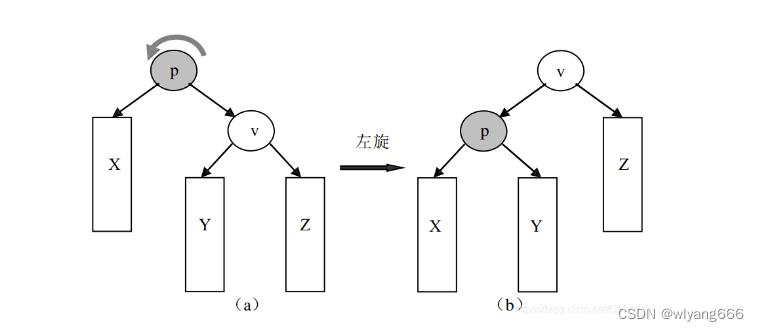
在这里插入图片描述

3.3.1 思路

左旋和右旋相反，代码类似。

3.3.2 代码

 /**
  * @param k2:最小不平衡子树
  * @return void
  * @Description:左旋
  * @Author: wanlong
  * @Date: 2023/6/5 18:46
  **/
 AVLNode<T> leftRotate(AVLNode k2) {
     AVLNode k1 = k2.right;
     k2.right = k1.left;
     k1.left = k2;
     k2.height = Math.max(height(k2.right), height(k2.left)) + 1;
     k1.height = Math.max(height(k1.right), k2.height) + 1;
     return k1;
 }

3.4 双旋LR

从之前的案例可以看到，当最小不平衡子树的根节点平衡因子为正，而它的左节点平衡因子是负的时候，此时需要进行双旋LR。

3.4.1 思路

在LR旋转中，我们需要先左旋，再右旋，左旋是保证节点的符号相同

3.4.2 代码

    /**
     * @param k2:
     * @return org.wanlong.tree.AVLNode<T>
     * @Description: LR型双旋转 先左旋，再右旋
     * @Author: wanlong
     * @Date: 2023/6/5 19:15
     **/
    AVLNode<T> leftRightRotate(AVLNode k2) {
        k2.left = leftRotate(k2.left);
        return rightRotate(k2);
    }

3.5 双旋RL

从之前的案例可以看到，当最小不平衡子树的根节点平衡因子为负，而它的右节点平衡因子是正的时候，此时需要进行双旋RL。

3.5.1 思路

在RL旋转中，我们需要先右旋，再左旋，右旋是保证节点的符号相同

3.5.2 代码

    /**
     * @param k2:
     * @return org.wanlong.tree.AVLNode<T>
     * @Description: RL型双旋转 先右旋，再左旋
     * @Author: wanlong
     * @Date: 2023/6/5 19:15
     **/
    AVLNode<T> rightLeftRotate(AVLNode k2) {
        k2.right = rightRotate(k2.right);
        return leftRotate(k2);
    }

3.6 完整代码

package org.wanlong.tree;

/**
 * @author wanlong
 * @version 1.0
 * @description: 平衡二叉查找树
 * @date 2023/6/1 15:47
 */
public class AVLTree<T extends Comparable<? super T>> {

    //根节点
    private AVLNode<T> root;

    //允许最大的不平衡因子
    private static final int ALLOWED_IMBALANCE = 1;

    //返回树的高度
    private int height(AVLNode<T> t) {
        return t == null ? -1 : t.height;
    }

    public boolean isEmpty() {
        return root == null;
    }

    public void makeEmpty() {
        root = null;
    }

    public T findMin() {
        return findMin(root).data;
    }

    public T findMax() {
        return findMax(root).data;
    }

    //插入节点
    public void insert(T x) {
        root = insert(x, root);
    }

    //删除节点
    public void remove(T x) {
        root = remove(x, root);
    }

    //以某节点为根节点，删除子树的对应节点
    private AVLNode<T> remove(T x, AVLNode<T> t) {

        if (null == t) {
            return t;
        }

        int compareResult = x.compareTo(t.data);

        //小于当前根节点
        if (compareResult < 0) {
            t.left = remove(x, t.left);
        } else if (compareResult > 0) {
            //大于当前根节点
            t.right = remove(x, t.right);
        } else if (t.left != null && t.right != null) {
            //找到右边最小的节点
            t.data = findMin(t.right).data;
            //当前节点的右边等于原节点右边删除已经被选为的替代节点
            t.right = remove(t.data, t.right);
        } else {
            t = (t.left != null) ? t.left : t.right;
        }
        return balance(t);
    }

    //以某节点为根节点，插入子树的对应节点
    private AVLNode<T> insert(T x, AVLNode<T> t) {

        //如果根节点为空，则当前x节点为根及诶单
        if (null == t) {
            return new AVLNode(x);
        }

        int compareResult = x.compareTo(t.data);

        //小于当前根节点 将x插入根节点的左边
        if (compareResult < 0) {
            t.left = insert(x, t.left);
        } else if (compareResult > 0) {
            //大于当前根节点 将x插入根节点的右边
            t.right = insert(x, t.right);
        } else {

        }
        return balance(t);
    }


    /**
     * @param t:
     * @return org.wanlong.tree.AVLNode<T>
     * @Description: 平衡节点方法
     * @Author: wanlong
     * @Date: 2023/6/5 19:58
     **/
    private AVLNode<T> balance(AVLNode<T> t) {
        if (t == null) {
            return t;
        }
        //左子树大于右子树 ，平衡因子大于1
        if (height(t.left) - height(t.right) > ALLOWED_IMBALANCE) {
            //左子树的左子树高度大于左子树的右子树高度 即根节点左节点的平衡因子和根节点一致 直接右旋
            if (height(t.left.left) >= height(t.left.right)) {
                t = rightRotate(t);
            } else {
                //左子树的左子树高度小于左子树的右子树高度 即根节点左节点的平衡因子为负数，和根节点相反 ，此时需要先左旋，再右旋
                t = leftRightRotate(t);
            }
            //右子树高度 大于 左子树，平衡因子小于 -1
        } else if (height(t.right) - height(t.left) > ALLOWED_IMBALANCE) {
            //右子树的右子树高度 大于 右子树的左子树高度 ，根节点右节点的平衡因子和根节点一致，直接左旋
            if (height(t.right.right) >= height(t.right.left)) {
                t = leftRotate(t);
            } else {
                //右子树的右子树高度 小于 右子树的左子树高度 ，根节点右节点的平衡因子和根节点相反，先右旋，再左旋
                t = rightLeftRotate(t);
            }
        }
        //重新计算树的高度
        t.height = Math.max(height(t.left), height(t.right)) + 1;
        return t;
    }


    /**
     * @param p: 最小不平衡子树
     * @return void
     * @Description:右旋
     * @Author: wanlong
     * @Date: 2023/6/5 18:36
     **/
    AVLNode<T> rightRotate(AVLNode p) {
        AVLNode k1 = p.left;
        p.left = k1.right;
        k1.right = p;
        p.height = Math.max(height(p.left), height(p.right)) + 1;
        k1.height = Math.max(height(k1.left), p.height) + 1;
        return k1;
    }


    /**
     * @param k2:最小不平衡子树
     * @return void
     * @Description:左旋
     * @Author: wanlong
     * @Date: 2023/6/5 18:46
     **/
    AVLNode<T> leftRotate(AVLNode k2) {
        AVLNode k1 = k2.right;
        k2.right = k1.left;
        k1.left = k2;
        k2.height = Math.max(height(k2.right), height(k2.left)) + 1;
        k1.height = Math.max(height(k1.right), k2.height) + 1;
        return k1;
    }

    /**
     * @param k2:
     * @return org.wanlong.tree.AVLNode<T>
     * @Description: LR型双旋转 先左旋，再右旋
     * @Author: wanlong
     * @Date: 2023/6/5 19:15
     **/
    AVLNode<T> leftRightRotate(AVLNode k2) {
        k2.left = leftRotate(k2.left);
        return rightRotate(k2);
    }

    /**
     * @param k2:
     * @return org.wanlong.tree.AVLNode<T>
     * @Description: RL型双旋转 先右旋，再左旋
     * @Author: wanlong
     * @Date: 2023/6/5 19:15
     **/
    AVLNode<T> rightLeftRotate(AVLNode k2) {
        k2.right = rightRotate(k2.right);
        return leftRotate(k2);
    }


    /**
     * @param root:
     * @return org.wanlong.tree.AVLNode<T>
     * @Description:找最小节点
     * @Author: wanlong
     * @Date: 2023/6/5 20:00
     **/
    private AVLNode<T> findMin(AVLNode<T> root) {
        if (root == null) {
            return null;
        } else if (root.left == null) {
            return root;
        }
        return findMin(root.left);
    }

    /**
     * @param root:
     * @return org.wanlong.tree.AVLNode<T>
     * @Description:找最大节点
     * @Author: wanlong
     * @Date: 2023/6/5 19:30
     **/
    private AVLNode<T> findMax(AVLNode<T> root) {
        if (root == null) {
            return null;
        } else if (root.right == null) {
            return root;
        } else {
            return findMax(root.right);
        }
    }


    /**
     * @return void
     * @Description: 打印
     * @Author: wanlong
     * @Date: 2023/6/5 19:31
     **/
    public void printTree() {
        if (isEmpty()) {
            System.out.println("节点为空");
        } else {
            printTree(root);
        }
    }

    /**
     * @return void
     * @Description: 打印
     * @Author: wanlong
     * @Date: 2023/6/5 19:31
     **/
    public void printTree(AVLNode<T> root) {
        if (root != null) {
            System.out.print(root.data);
            if (null != root.left) {
                System.out.print("左边节点" + root.left.data);
            }
            if (null != root.right) {
                System.out.print("右边节点" + root.right.data);
            }
            System.out.println();
            printTree(root.left);
            printTree(root.right);
        }
    }
}

4. 测试验证

@Test
public void testAVLTree(){
    //3，2，1，4，5，6，7，10，9，8
    AVLTree<Integer> tree = new AVLTree<>();
    int[] array=new int[]{3,2,1,4,5,6,7,10,9,8};
    for (int i : array) {
        tree.insert(i);
    }
    tree.printTree();
    System.out.println("=====");
    Integer min = tree.findMin();
    Integer max = tree.findMax();
    System.out.println("min:"+min);
    System.out.println("max:"+max);
}

代码运行结果：

4左边节点2右边节点7
2左边节点1右边节点3
1
3
7左边节点6右边节点9
6左边节点5
5
9左边节点8右边节点10
8
10
=====
min:1
max:10

可以看到，和下图预期结果一致：
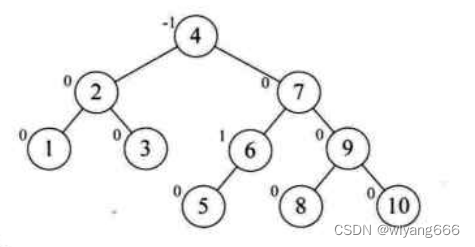
在这里插入图片描述

5. 参考资料：

国外数据结构演示网站
大话数据结构图书
java实现AVL树

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/613009.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

华为OD机试真题 Java 实现【玩牌高手】【2023 B卷 100分】，附详细解题思路

华为OD机试真题 Java 实现【玩牌高手】【2023 B卷 100分】，附详细解题思路

一、题目描述 给定一个长度为n的整型数组&#xff0c;表示一个选手在n轮内可选择的牌面分数。选手基于规则选牌&#xff0c; 请计算所有轮结束后其可以获得的最高总分数。 选择规则如下&#xff1a; 在每轮里选手可以选择获取该轮牌面&#xff0c;则其总分数加上该轮牌面分…
阅读更多...
python笔记 第二章 变量

python笔记 第二章 变量

系列文章目录 第一章 初识python 文章目录 2.1变量2.1.1变量的作用2.1.2定义变量标识符命名习惯使用变量 2.2 认识bugDebug工具Debug工具使用步骤: 2.3 数据类型 2.1变量 目标 变量的作用定义变量认识数据类型 2.1.1变量的作用 变量就是一个存储数据的的时候当前数据所在的…
阅读更多...
Java基础——堆和栈、static关键字、静态变量和成员变量的区别

Java基础——堆和栈、static关键字、静态变量和成员变量的区别

Java程序运行顺序&#xff1a;Java应用程序—虚拟机—操作系统—硬件 Java中栈内存用来存储局部变量和方法调用&#xff0c;堆内存用来存储Java中的对象&#xff0c;成员变量、局部变量、类变量指向的对象都存储在堆内存中。 static关键字&#xff1a; 随着类的加载而加载优先…
阅读更多...
ISATAP隧道配置与验证

ISATAP隧道配置与验证

ISATAP隧道配置与验证 【实验目的】 熟悉IPv6ISATAP隧道的概念。 掌握IPv6和IPv4共存的实现方法。 掌握IPv6 ISATAP地址编址规则。 掌握IPv6 ISATAP隧道的配置。 验证配置。 【实验拓扑】 设备参数如下表所示。 设备 接口 IP地址 子网掩码 默认网关 R1 S0/0 192.…
阅读更多...
【内存管理大猫腻：从“越界”到“内存泄漏”应有尽有】

【内存管理大猫腻：从“越界”到“内存泄漏”应有尽有】

本章重点 什么是动态内存 为什么要有动态内存 什么是野指针 对应到C空间布局&#xff0c; malloc 在哪里申请空间 常见的内存错误和对策 C中动态内存“管理”体现在哪 什么是动态内存 动态内存是指在程序运行时&#xff0c;根据需要动态分配的内存空间。 #include <stdio.h&…
阅读更多...
1.链表的实现：不带哨兵

1.链表的实现：不带哨兵

一、链表linked list 1.定义 链表是数据元素的线性集合&#xff0c;其每个元素都指向下一个元素&#xff0c;元素存储上并不连续,链表逻辑连续。 2.分类 ①单向链表&#xff1a;每个元素只知道其下一个元素是谁 ②双向链表: 每个元素知道其上一个元素和下一个元素 ③循环链…
阅读更多...
Java - Stream流详解

Java - Stream流详解

文章目录 前言 大家好,好久不见了,最近由于实训的影响导致拖更了,在更新这一次估计javaSE基本上就算是完结了,还有一些落下的后面也会补上的,下次见面就是数据结构了 尽情期待吧!那么就让我们步入Stream流的学习吧! 一、Stream流是什么&#xff1f; Stream流是Java 8中的一个…
阅读更多...
【openEuler 20.03 TLS编译openGauss2.0.0源码】

【openEuler 20.03 TLS编译openGauss2.0.0源码】

openEuler 20.03 TLS编译openGauss2.0.0源码 一、安装环境二、安装前准备二、安装步骤 一、安装环境 项目Value操作系统openEuler 20.03 64bit with ARMopenGauss2.0.0openGauss-third_party2.0.0 二、安装前准备 项目Value购买华为ECS鲲鹏 8vCPU32G 100M/s带宽 openEuler 2…
阅读更多...
使用CubeMX配置STM32驱动HC-SR04超声波模块

使用CubeMX配置STM32驱动HC-SR04超声波模块

文章目录 前言1 使用STM32CubeMX初始化代码1.1 时钟配置1.2 设置定时器1.3 触发引脚1.4 串口配置 2 代码编写2.1 添加驱动文件2.2 修改main.c 3 实现效果参考 前言 硬件选择 stm32f103c8t6&#xff08;最小板&#xff09;hc-sr04超声波模块 软件环境 stm32cubeIDE 1.12.1 …
阅读更多...
【Linux】TCP网络套接字编程+协议定制+序列化和反序列化

【Linux】TCP网络套接字编程+协议定制+序列化和反序列化

悟已往之不谏&#xff0c;知来者之可追。抓不住的就放手&#xff0c;属于你的都在路上…… 文章目录 一、TCP网络套接字编程1.日志等级分类的日志输出API2.单进程版本的服务器客户端通信3.多进程版本和多线程版本4.线程池版本5.守护进程化的线程池服务器6.三次握手和四次挥手的…
阅读更多...
python编程——pycharm的安装与使用

python编程——pycharm的安装与使用

作者&#xff1a;Insist-- 个人主页&#xff1a;insist--个人主页 本文专栏&#xff1a;python专栏 专栏介绍&#xff1a;本专栏为免费专栏&#xff0c;并且会持续更新python基础知识&#xff0c;欢迎各位订阅关注。 目录 一、python IDLE的使用 二、pycharm的安装与使用 1、…
阅读更多...
十分钟带你看懂——Python测试框架之pytest最全讲

十分钟带你看懂——Python测试框架之pytest最全讲

pytest特短 pytest是一个非常成熟的全功能的Python测试框架&#xff0c;主要有以下几个特点&#xff1a; 简单灵活&#xff0c;容易上手 支持参数化 能够支持简单的单元测试和复杂的功能测试&#xff0c;还可以用来做selenium/appnium等自动化测试、接口自动化测试&#xff08…
阅读更多...
重磅版本发布｜三大关键特性带你认识 Milvus 2.2.9 ：JSON、PartitionKey、Dynamic Schema

重磅版本发布｜三大关键特性带你认识 Milvus 2.2.9 ：JSON、PartitionKey、Dynamic Schema

亮点颇多、精彩程度堪比大版本的 Milvus 2.2.9 来啦&#xff01; 随着 LLM 的持续火爆&#xff0c;众多应用开发者将目光投向了向量数据库领域&#xff0c;而作为开源向量数据库的领先者&#xff0c;Milvus 也充分吸收了大量来自社区、用户、AI 从业者的建议&#xff0c;把重心…
阅读更多...
非常简单就能理解的 链表带环问题 你也能轻松学会！

非常简单就能理解的 链表带环问题 你也能轻松学会！

文章目录 判断链表是否带环若链表带环找出环的入口其他高频的面试问题 判断链表是否带环 题目描述&#xff1a; 给定一个链表&#xff0c;判断链表中是否有环。 思路&#xff1a; 可以明确的是&#xff1a;若一个链表带环&#xff0c;那么用指针一直顺着链表遍历&#xff0c…
阅读更多...
《嵌入式系统》知识总结10：使用位带操作操纵GPIO

《嵌入式系统》知识总结10：使用位带操作操纵GPIO

位操作 汇编层面 外设控制常要针对字中某个位&#xff08;Bit&#xff09;操作 以字节编址的存储器地址空间中&#xff0c;需要3步骤&#xff08;读出-修改-写回&#xff09; 1.&#xff08;从外设&#xff09;读取包含该位的字节数据 2. 设置该位为0或1、同时屏蔽其他位&am…
阅读更多...
微信小程序 ＜view＞＜/view＞容器嵌套，wxss样式修改内部内部样式不产生效果

微信小程序 ＜view＞＜/view＞容器嵌套，wxss样式修改内部内部样式不产生效果

网上关于”微信小程序讲的知识很少“&#xff0c;微信开发文档对于新手不是很友好&#xff0c;但是建议一定要学会看文档。 问题如下&#xff1a; 我写了好几个<view></view> 容器嵌套&#xff0c;我在对内部容器包括的内容做修改时&#xff0c;不产生效果&#…
阅读更多...
apache RocketMQ远程代码执行（CVE-2023-33246）

apache RocketMQ远程代码执行（CVE-2023-33246）

RocketMQ是阿里巴巴在2012年开发的分布式消息中间件&#xff0c;专为万亿级超大规模的消息处理而设计&#xff0c;具有高吞吐量、低延迟、海量堆积、顺序收发等特点。它是阿里巴巴双十一购物狂欢节和众多大规模互联网业务场景的必备基础设施。 RocketMQ的NameServer、Broker、…
阅读更多...
【计算机网络之HTTP篇】Cookie与Session的区别

【计算机网络之HTTP篇】Cookie与Session的区别

目录 Cookie 原理 缺点 Session 原理 区别 Cookie cookie是浏览器在本地存储数据的一种机制。 原理 当浏览器向服务器第一次发送请求时&#xff0c;服务器会向浏览器返回一个Cookie&#xff0c;此时 cookie记录着浏览器访问服务器的用户登录状态。 后续浏览器再次访问服…
阅读更多...
[深度学习入门案例1]基于Keras的手写数字图像识别

[深度学习入门案例1]基于Keras的手写数字图像识别

文章目录 一、工具与环境 二、深度学习环境的搭建 1.安装Anaconda 2.创建虚拟环境 第1步&#xff1a;打开Anaconda的命令窗口&#xff0c;即Anaconda Prompt 第2步&#xff1a;使用命令创建指定版本的python环境&#xff08;这里以py36命令环境名称举例&#xff09; 3.切换…
阅读更多...
深度解析MethodHandle方法句柄之findspecial方法的原理

深度解析MethodHandle方法句柄之findspecial方法的原理

网上看过太多关于MethodHandle方法句柄的文章&#xff0c;但是基本上没有人能把其中的findspecial方法讲清楚&#xff0c;特别是findspecial的第四个参数specialCaller, 相信大家都不明白是干嘛用的&#xff0c;网上给出的水文是很多都是说&#xff1a; 执行到specialCaller的父…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023