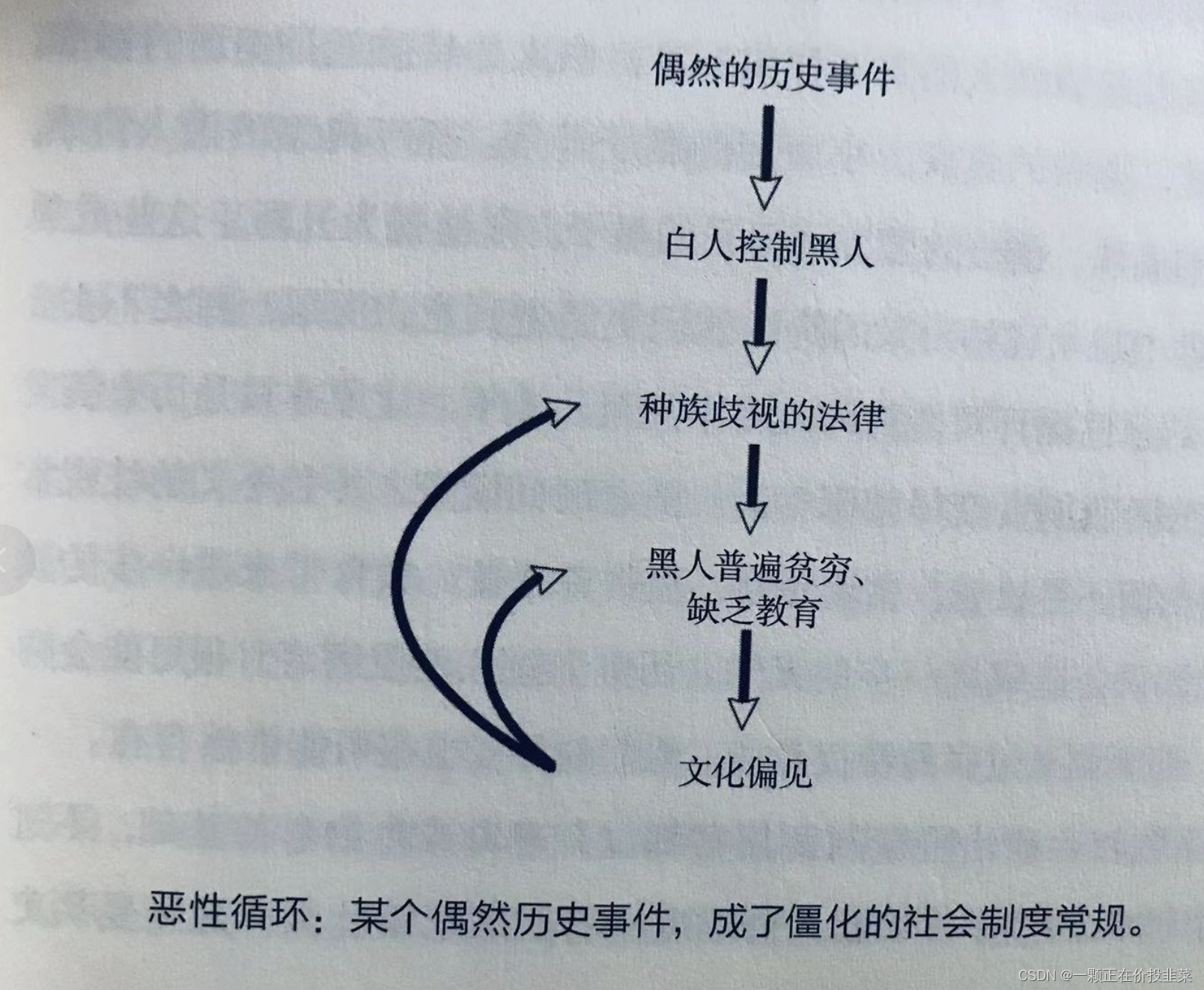
一、多元分类
之前讨论的神经网络都是以二元分类为目的进行介绍的。
当我们有不止两种分类时(也就是 y = 1 , 2 , 3 … . y=1,2,3…. y=1,2,3….),比如以下这种情况,该怎么办?如果我们要训练一个神经网络算法来识别路人、汽车、摩托车和卡车,在输出层我们应该有4个值。例如,第一个值为1或0用于预测是否是行人,第二个值用于判断是否为汽车。
输入向量
x
x
x有三个维度,两个中间层,输出层4个神经元分别用来表示4类,也就是每一个数据在输出层都会出现
[
a
b
c
d
]
T
{{\left[ a\text{ }b\text{ }c\text{ }d \right]}^{T}}
[a b c d]T,且
a
,
b
,
c
,
d
a,b,c,d
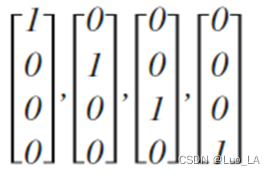
a,b,c,d中仅有一个为1,表示当前类。下面是该神经网络的可能结构示例:

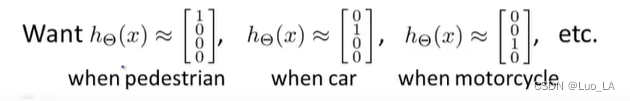
神经网络算法的输出结果为四种可能情形之一:
二、代价函数
首先引入一些便于稍后讨论的新标记方法:
假设神经网络的训练样本有
m
m
m个,每个包含一组输入
x
x
x和一组输出信号
y
y
y,
L
L
L表示神经网络层数,
S
I
S_I
SI表示每层的neuron个数(
S
l
S_l
Sl表示输出层神经元个数),
S
L
S_L
SL代表最后一层中处理单元的个数。
将神经网络的分类定义为两种情况:二类分类和多类分类,
二类分类:
S
L
=
0
,
y
=
0
o
r
1
S_L=0, y=0\, or\, 1
SL=0,y=0or1表示哪一类;
K
K
K类分类:
S
L
=
k
,
y
i
=
1
S_L=k, y_i = 1
SL=k,yi=1表示分到第
i
i
i类;
(
k
>
2
)
(k>2)
(k>2)
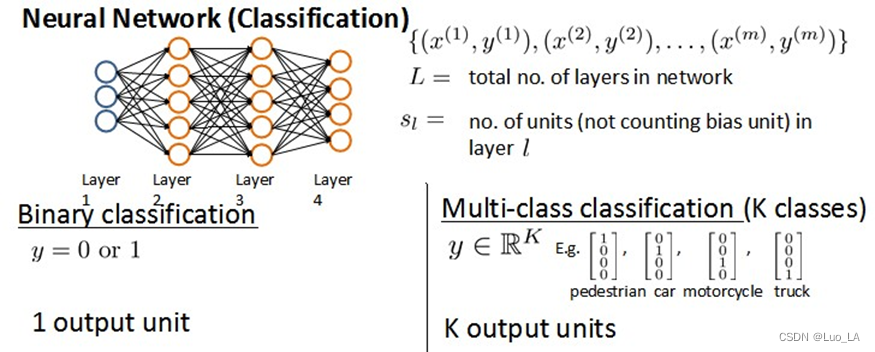
我们回顾逻辑回归问题中我们的代价函数为:
J
(
θ
)
=
1
m
∑
i
=
1
m
[
−
y
(
i
)
log
(
h
θ
(
x
(
i
)
)
)
−
(
1
−
y
(
i
)
)
log
(
1
−
h
θ
(
x
(
i
)
)
)
]
+
λ
2
m
∑
j
=
1
n
θ
j
2
J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{[-{{y}^{(i)}}\log \left( {h_\theta}\left( {{x}^{(i)}} \right) \right)-\left( 1-{{y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( {{x}^{(i)}} \right) \right)]}+\frac{\lambda }{2m}\sum\limits_{j=1}^{n}{\theta _{j}^{2}}
J(θ)=m1i=1∑m[−y(i)log(hθ(x(i)))−(1−y(i))log(1−hθ(x(i)))]+2mλj=1∑nθj2
在逻辑回归中,我们只有一个输出变量,又称标量(scalar),也只有一个因变量
y
y
y,但是在神经网络中,我们可以有很多输出变量,我们的
h
θ
(
x
)
h_\theta(x)
hθ(x)是一个维度为
K
K
K的向量,并且我们训练集中的因变量也是同样维度的一个向量,因此我们的代价函数会比逻辑回归更加复杂一些,为:
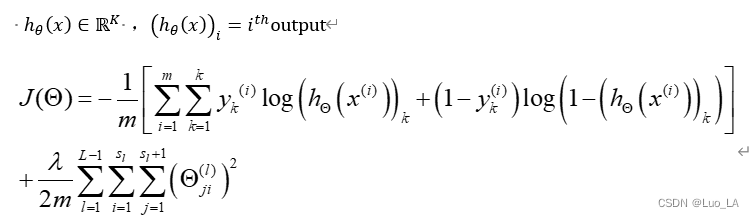
(
h
θ
(
x
)
)
i
{\left({h_\theta}\left(x\right)\right)}_{i}
(hθ(x))i 表示第
i
i
i个输出,也就是说
h
θ
(
x
)
h_\theta\left(x\right)
hθ(x)是一个k维向量。
这个看起来复杂很多的代价函数背后的思想还是一样的,我们希望通过代价函数来观察算法预测的结果与真实情况的误差有多大,唯一不同的是,对于每一行特征,我们都会给出 K K K个预测,基本上我们可以利用循环,对每一行特征都预测 K K K个不同结果,然后再利用循环在 K K K个预测中选择可能性最高的一个,将其与 y y y中的实际数据进行比较。
正则化的那一项只是排除了每一层 θ 0 \theta_0 θ0后,每一层的 θ \theta θ 矩阵的和。最里层的循环 j j j循环所有的行(由 s l + 1 s_{l+1} sl+1 层的激活单元数决定),循环 i i i则循环所有的列,由该层( s l s_l sl层)的激活单元数所决定。即: h θ ( x ) h_\theta(x) hθ(x)与真实值之间的距离为每个样本-每个类输出的加和,对参数进行regularization的bias项处理所有参数的平方和。
三、反向传播算法
下面介绍一个让代价函数最小化的算法——反向传播算法(Backpropagation Algorithm)。
之前我们在计算神经网络预测结果的时候我们采用了一种正向传播方法,我们从第一层开始正向一层一层进行计算,直到最后一层的 h θ ( x ) h_{\theta}\left(x\right) hθ(x)。
以一个例子来说明:
假设我们的训练集只有一个样本
(
x
(
1
)
,
y
(
1
)
)
\left({x}^{(1)},{y}^{(1)}\right)
(x(1),y(1)),我们的神经网络是一个四层的神经网络,其中
K
=
4
,
S
L
=
4
,
L
=
4
K=4,S_{L}=4,L=4
K=4,SL=4,L=4:
前向传播算法:

这里实现了把前向传播向量化,使得我们可以计算神经网络里面的每一个神经元的激活值。前向传播见这篇文章 机器学习——神经网络介绍及模型表示
现在,为了计算代价函数的偏导数 ∂ ∂ Θ i j ( l ) J ( Θ ) \frac{\partial}{\partial\Theta^{(l)}_{ij}}J\left(\Theta\right) ∂Θij(l)∂J(Θ),我们需要采用一种反向传播算法,也就是首先计算最后一层的误差,然后再一层一层反向求出各层的误差,直到倒数第二层。
我们用 δ \delta δ来表示误差, δ j ( l ) \delta^{(l)}_j δj(l) 表示第 l l l层第 j j j个节点的误差。
我们从最后一层(输出层)的误差开始计算,误差是激活单元的预测(
a
(
4
)
{a^{(4)}}
a(4))与实际值(
y
k
y^k
yk)之间的误差,(
k
=
1
:
k
k=1:k
k=1:k)。
对于每一个输出层的节点:
δ
j
(
4
)
=
a
i
(
4
)
−
y
i
\delta^{(4)}_j=a^{(4)}_i-y_i
δj(4)=ai(4)−yi
把
δ
,
a
,
j
\delta,a,j
δ,a,j都看作向量,则有:
δ
(
4
)
=
a
(
4
)
−
y
\delta^{(4)}=a^{(4)}-y
δ(4)=a(4)−y
我们利用这个误差值来计算前一层的误差:
δ
(
3
)
=
(
Θ
(
3
)
)
T
δ
(
4
)
∗
g
′
(
z
(
3
)
)
\delta^{(3)}=\left({\Theta^{(3)}}\right)^{T}\delta^{(4)}\ast g'\left(z^{(3)}\right)
δ(3)=(Θ(3))Tδ(4)∗g′(z(3))
其中
g
′
(
z
(
3
)
)
g'(z^{(3)})
g′(z(3))是
S
S
S 形函数的导数,我们通过计算可以得到:
g
′
(
z
(
3
)
)
=
a
(
3
)
∗
(
1
−
a
(
3
)
)
g'(z^{(3)})=a^{(3)}\ast(1-a^{(3)})
g′(z(3))=a(3)∗(1−a(3))。而
(
θ
(
3
)
)
T
δ
(
4
)
(θ^{(3)})^{T}\delta^{(4)}
(θ(3))Tδ(4)则是权重导致的误差的和。
下一步是继续计算第二层的误差: δ ( 2 ) = ( Θ ( 2 ) ) T δ ( 3 ) ∗ g ′ ( z ( 2 ) ) \delta^{(2)}=(\Theta^{(2)})^{T}\delta^{(3)}\ast g'(z^{(2)}) δ(2)=(Θ(2))Tδ(3)∗g′(z(2))
因为第一层是输入变量,不存在误差。我们有了所有的误差的表达式后,便可以计算代价函数的偏导数了,假设
λ
=
0
λ=0
λ=0,即我们不做任何正则化处理时有:
∂
∂
Θ
i
j
(
l
)
J
(
Θ
)
=
a
j
(
l
)
δ
i
l
+
1
\frac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta)=a_{j}^{(l)} \delta_{i}^{l+1}
∂Θij(l)∂J(Θ)=aj(l)δil+1
我们不需要知道上面式子的推导过程,重要的是清楚地知道上面式子中上下标的含义:
l
l
l 代表目前所计算的是第几层。
j
j
j 代表目前计算层中的激活单元的下标,也将是下一层的第
j
j
j个输入变量的下标。
i
i
i 代表下一层中误差单元的下标,是受到权重矩阵中第
i
i
i行影响的下一层中的误差单元的下标。
想了解一下反向传播算法的具体计算过程的,可以参考一下李宏毅老师的机器学习视频中对反向传播算法的讲解李宏毅2021/2022春机器学习课程
————————————————————————————————————————
上面介绍的是以一个训练样本为例的反向传播算法,当我们有一个非常大的训练样本(m个)的时候,我们同样需要计算每一层的误差单元,但是我们需要为整个训练集计算误差单元,此时的误差单元也是一个矩阵。
我们用
Δ
i
j
(
l
)
\Delta^{(l)}_{ij}
Δij(l)来表示这个误差矩阵:第
l
l
l 层的第
i
i
i 个激活单元受到第
j
j
j 个参数影响而导致的误差。
我们的算法表示为:

即首先用正向传播方法计算出每一层的激活单元,利用训练集的结果与神经网络预测的结果求出最后一层的误差,然后利用该误差运用反向传播法计算出直至第二层的所有误差。
注意:
f
o
r
for
for循环中的
i
i
i和
Δ
i
j
(
l
)
\Delta^{(l)}_{ij}
Δij(l)中的
i
i
i表示的含义是不一样的,前者是用于循环,表示的是训练样本中的第
i
i
i组数据;后者的下标
i
i
i不参与循环,代表某一层的第
i
i
i个激活单元
在求出了
Δ
i
j
(
l
)
\Delta_{ij}^{(l)}
Δij(l)之后,我们便可以计算代价函数的偏导数了,计算方法如下:
D
i
j
(
l
)
:
=
1
m
Δ
i
j
(
l
)
+
λ
Θ
i
j
(
l
)
D_{ij}^{(l)} :=\frac{1}{m}\Delta_{ij}^{(l)}+\lambda\Theta_{ij}^{(l)}
Dij(l):=m1Δij(l)+λΘij(l)
i
f
j
≠
0
{if}\; j \neq 0
ifj=0
D i j ( l ) : = 1 m Δ i j ( l ) D_{ij}^{(l)} :=\frac{1}{m}\Delta_{ij}^{(l)} Dij(l):=m1Δij(l) i f j = 0 {if}\; j = 0 ifj=0
计算出代价函数的偏导数之后,我们就可以利用梯度下降的方法计算最小代价函数了。

![[附源码]计算机毕业设计网上鲜花购物系统Springboot程序](https://img-blog.csdnimg.cn/daa309c783fe45439d301c5cefa1c0ee.png)

![[附源码]计算机毕业设计基于SpringBoot的党务管理系统](https://img-blog.csdnimg.cn/ecb6f2d98eb74baf80dc334ede819a74.png)