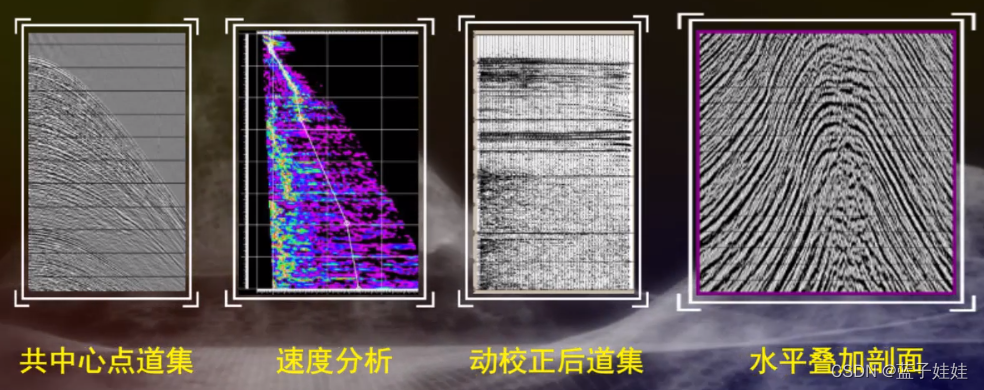
速度分析
在地震资料数字处理中,速度分析是动校正和水平叠加和地震偏移的基础。
在水平界面情况下,共中心点时距曲线方程是一条双曲线。在共中心点时距曲线中,炮检距 x x x 和时间 t 0 t_0 t0 都是已知的,只有速度 v v v 是未知的。
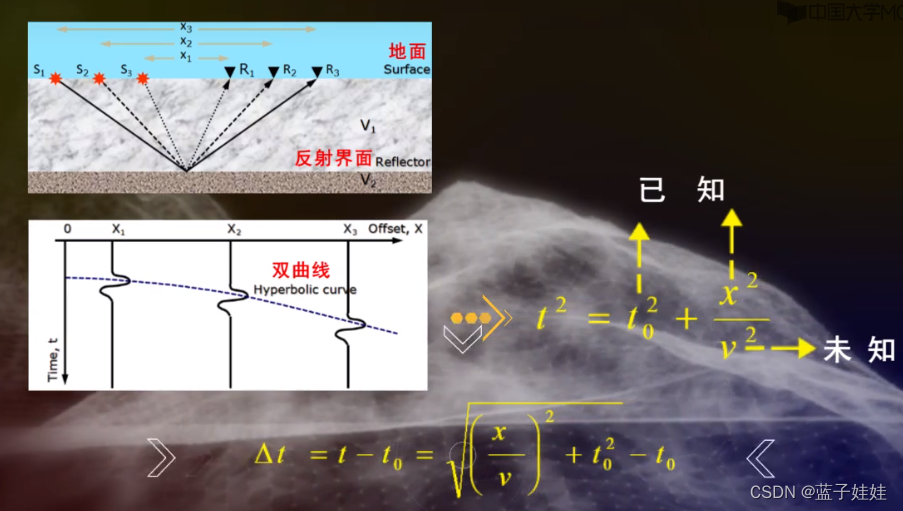
地震速度分析就是利用速度扫描对地震数据进行正常时差校正,通过将反射波同相轴拉平,求取叠加速度或动校正速度的方法。

反射波的时距曲线在 t t t- x x x 坐标下是双曲线,在 t 2 t^2 t2- x 2 x^2 x2 下是直线。只要求出直线的斜率,就可估算出地震速度。这种方法很简单但是计算精度不高,现在很少使用。
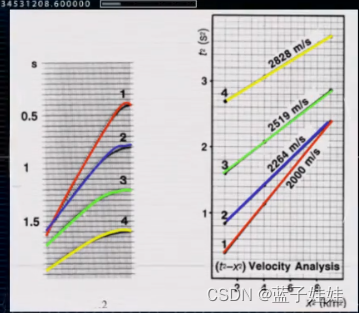
目前常用的速度分析方法叫做速度谱,类似于频谱。频谱表示不同频率地震波的能量变化,速度谱表示不同叠加速度随叠加或者相关的能量变化。
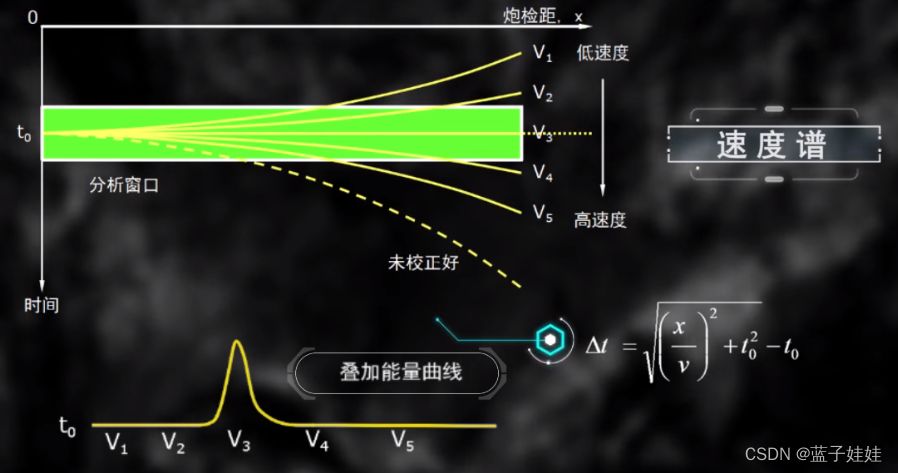
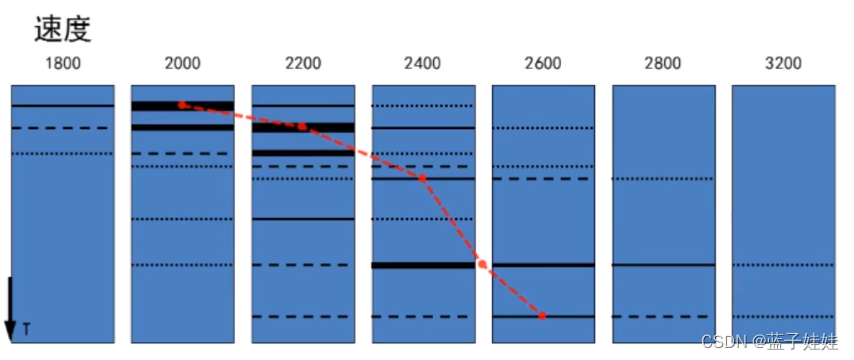
在一个共中心点道集中,固定某一个 t 0 t_0 t0,让炮检距 x x x 变化,任意给一个叠加速度 v 1 v_1 v1,可以计算出动校正量,计算之后再进行动校正,然后水平叠加得到一个叠加能量 A 1 A_1 A1。以此类推,可以得到叠加能量 A 随着叠加速度 V的变化曲线。这条曲线成为速度谱曲线。从下图所示的速度谱曲线可知,当速度为 v 3 v_3 v3 时,刚好可以将双曲线校直,叠加能量对应是最大值。从速度谱上找到叠加能量的最大值就是某一个 t 0 t_0 t0 处的动校正速度。
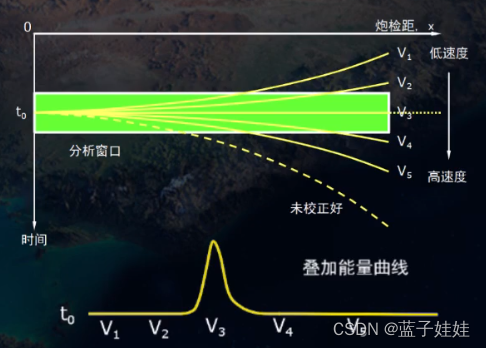
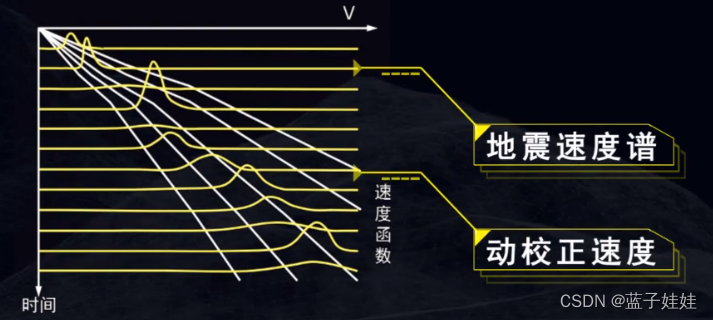
对于另外一个 t 0 t_0 t0,按照上述方法,同样可以得到一条速度谱曲线。以此类推,可以得到随 t 0 t_0 t0 变化的一系列速度谱线。从浅到深排列就是地震速度谱。从浅到深可以解释出多条速度函数曲线,其中有一条就是该共中心点道集从浅到深所用的动校正速度。
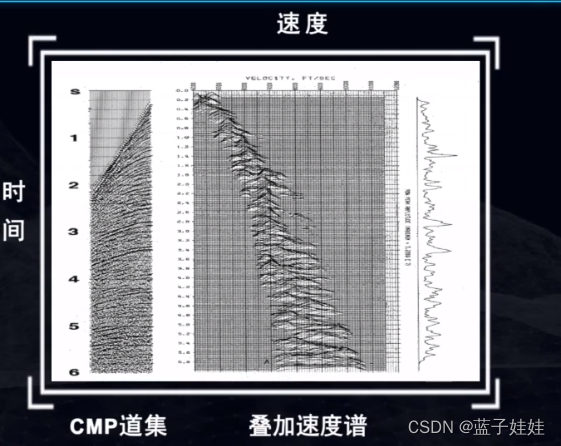
下图展示了一张实际的共中心点道集计算的速度谱。
速度谱还可以使用等值线形式表示,不同颜色表示不同的叠加能量。
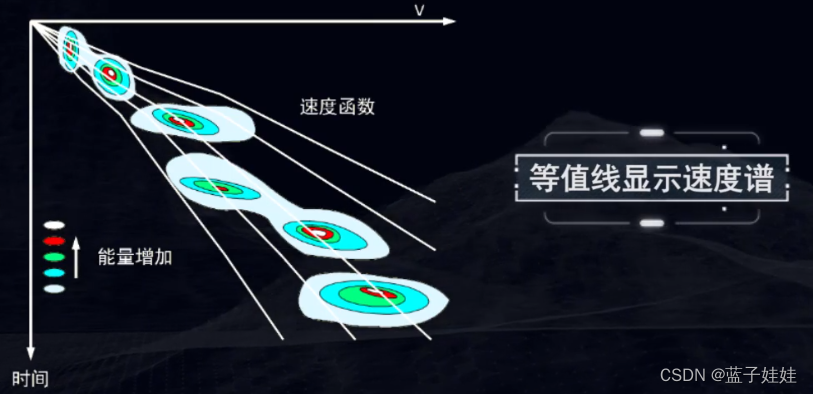
速度谱还可以使用彩色显示,不同颜色代表不同能量大小。

下图显示了一张制作叠加速度谱的程序设计框图。
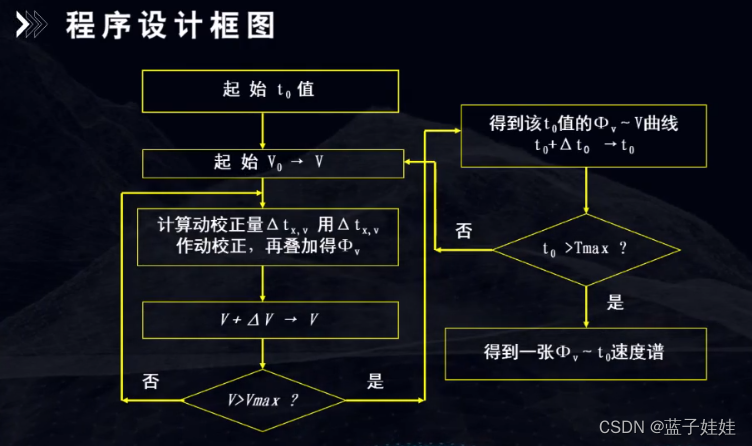
影响速度分析的精度和分辨率的因素有多种,主要包括近地表,地下地质因素和地震采集因素。
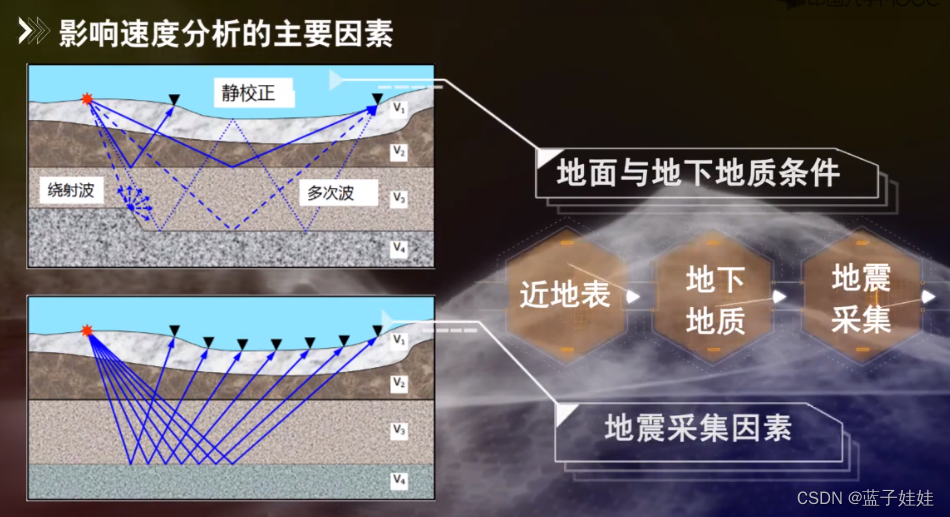

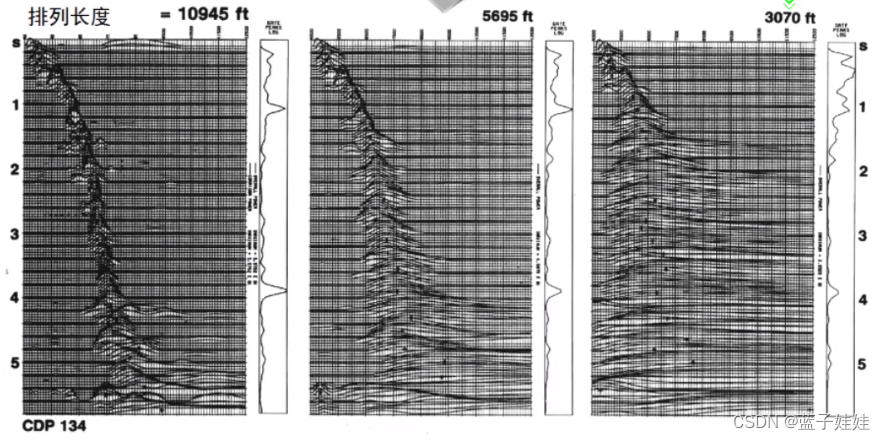
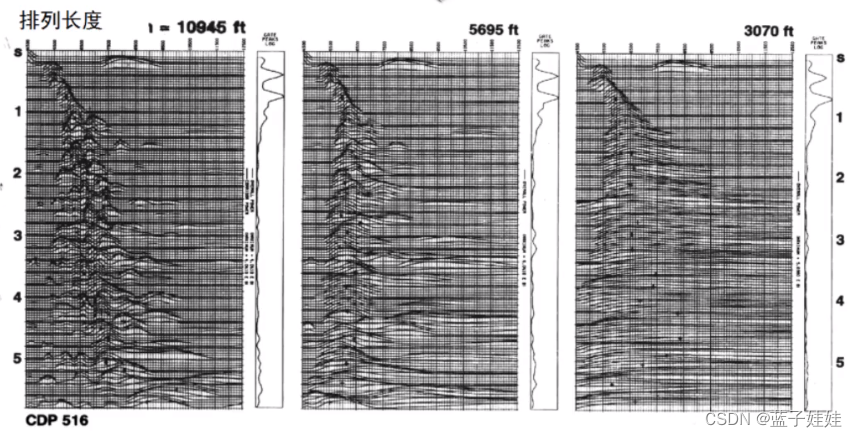
排列长度对速度谱有一定的影响,排列长度太短,速度谱分辨率会降低。例如在下图例子中,0-350m,0-750m的排列长度下,深层的速度分辨率较差。
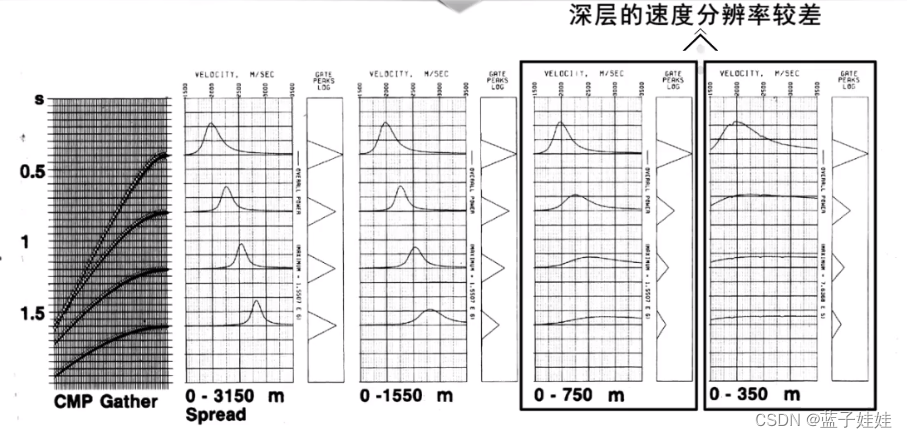
在下图例子中,排列长度为3070时,速度谱的深层分辨率降低。
近地表产生的静校正问题对速度分析影响也较大,如果静校正没有做好,速度分辨率会受到较大的影响。
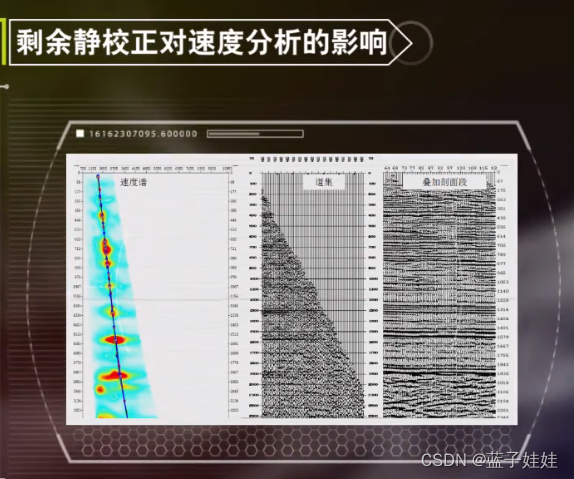
下图显示了某地区剩余静校正前的速度谱,动校正后的道集和叠加剖面由于存在剩余静校正,动校正后道集的分辨率不高,导致叠加剖面横向断断续续。
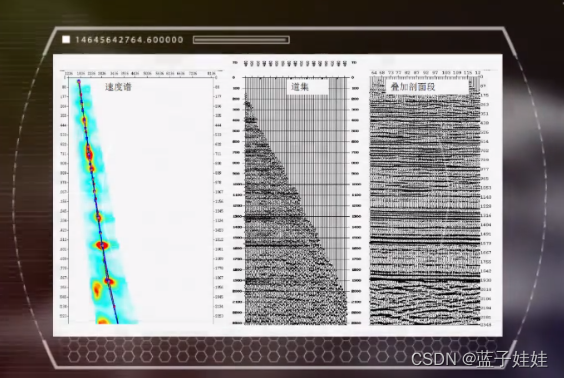
下图展示了剩余静校正后的速度谱,由于进行了剩余静校正,动校正后的道集分辨率提高,地震剖面上可以清晰对比解释。
如果只用大炮检距的资料进行速度谱分析,浅层的速度完全拾取不到,大小炮检距都用的情况下,速度分析效果较佳。
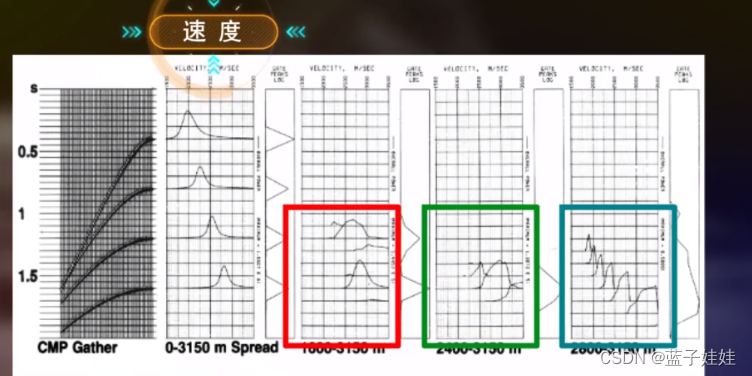
随着覆盖次数的增加,速度谱的质量会随之提高。过低的覆盖次数无法保证速度谱的质量。在实际应用中,可以采取相邻几个面元组成的宏面元进行分析。
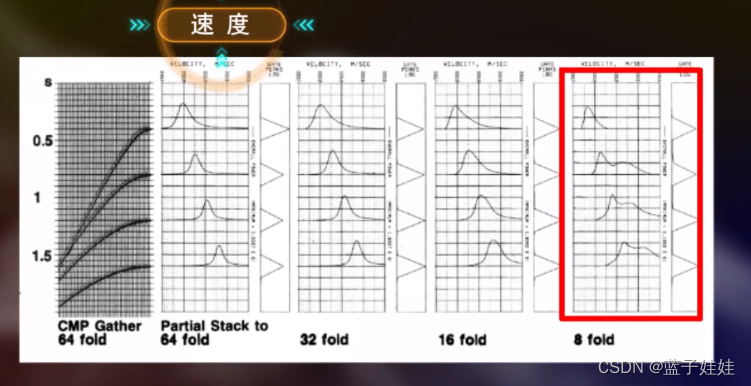
下图展示了信噪比为6,3,1的共中心点道集和对应的速度谱。

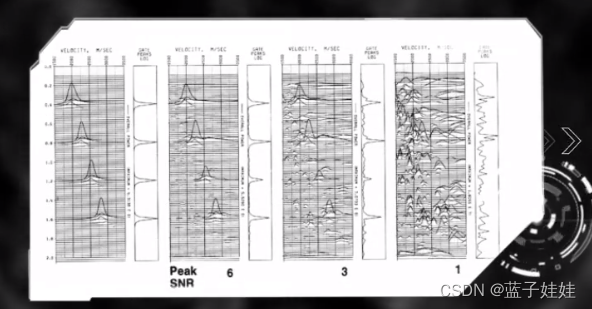
从速度谱可以看出,信噪比越高,速度分析的精度越高。
动校正会造成拉伸畸变波形,应该仔细选择切除参数。共中心点道集动校正拉伸畸变切除补偿后的速度谱就比切除未补偿的分辨率要高。
速度扫描范围应该包括所有的一次反射波速度。频带宽度也影响速度谱的精度,频带越宽,速度分辨率越高。为了提高速度分析的质量,可以对速度分析的道集进行一些必要的提高分辨率和提高信噪比的处理。
除了利用速度谱进行速度分析以外,还有一些辅助的手段对速度进行分析和提取。例如常速动校正扫描,常速动校正叠加扫描和沿层速度分析。
常速动校正扫描(CVP)是对某一个共中心点道集的记录用一系列恒定速度进行NMO校正。对于M个试验速度,就可以得到M个校正后的道集,将它们按照速度大小排列,校正后的各个道集同相轴校直的速度就是 t 0 t_0 t0时刻对应的叠加速度值。CVP方法简单快速,但是该方法存在速度拾取的不确定问题。
常速动校正叠加扫描方法 (CVS) 是在CVP的基础上,得到与速度个数相等的叠加剖面,将它们按照速度大小排列起来,然后从 CVS 中选出最佳叠加速度。实际处理中,常把速度谱和常速动校正叠加扫描一起处理和显示,这样可以取长补短,确定最佳的叠加速度。
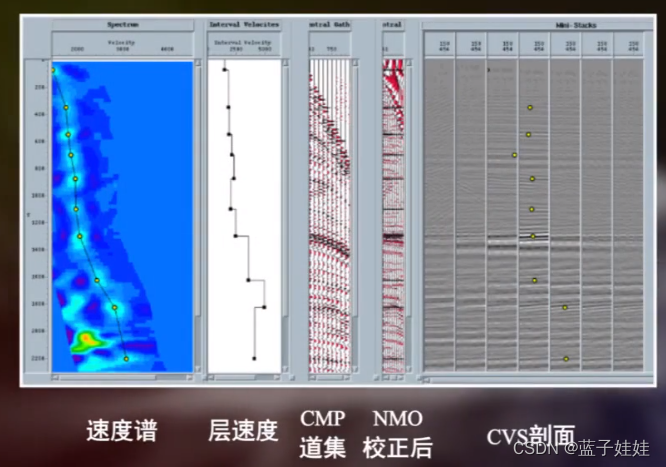
为了研究沿着某个或者几个反射层的叠加速度情况,还可以沿着反射层,以反射层在叠加剖面上的 t 0 t_0 t0 为中心取一时窗进行叠加速度分析,称为沿层速度分析。

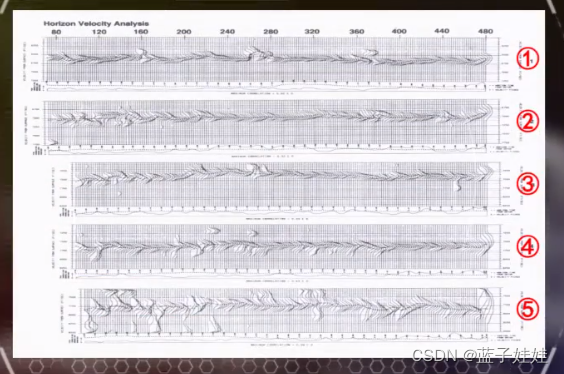
在地下界面时倾斜的情况下,除了要进行 NMO 校正外,还要进行 DMO (倾角)校正,在DMO校正后的速度谱要比校正前的分辨率高很多。
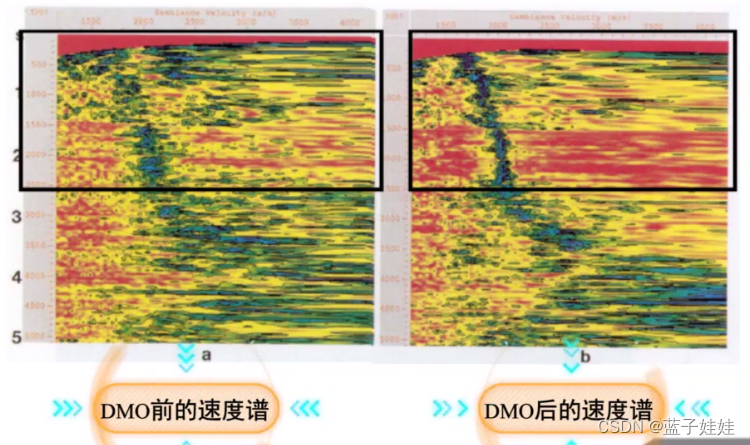
在地震资料数字处理过程中,针对水平层状介质,炮检距远大于反射界面深度之半的条件下,利用地震波时距曲线方程泰勒展开式的高次项进行的速度分析称为高阶速度分析。采用公式的前三项可以进行四次项速度分析。采用公式的前四项可以进行六次项速度分析。
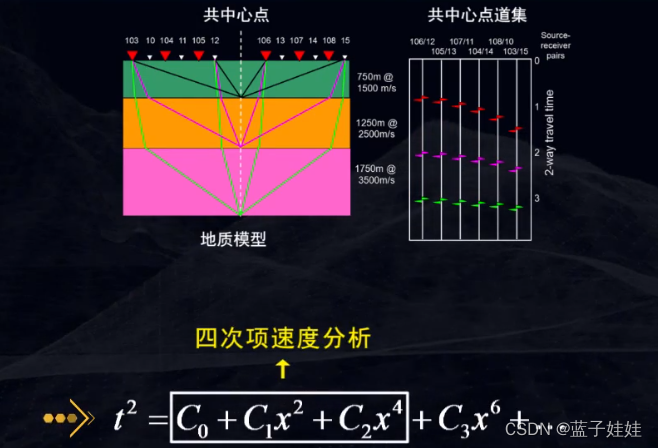
以上考虑的是二维速度分析,三维地震速度分析还要考虑 CDP 面元,方位角和地层倾角等因素的影响。