背包DP-入门篇

news2024/11/16 7:41:10

目录

01背包：

完全背包：

多重背包：

分组背包：

01背包：

[NOIP2005 普及组] 采药 - 洛谷https://www.luogu.com.cn/problem/P1048

01背包背景

在一个小山上，有个n个黄金和一个容量为w的背包，每块黄金有体积和价值两种属性，我们想要选若干黄金装入背包，使背包中黄金的总价值最大且不超过背包容量。

 闫式DP分析法：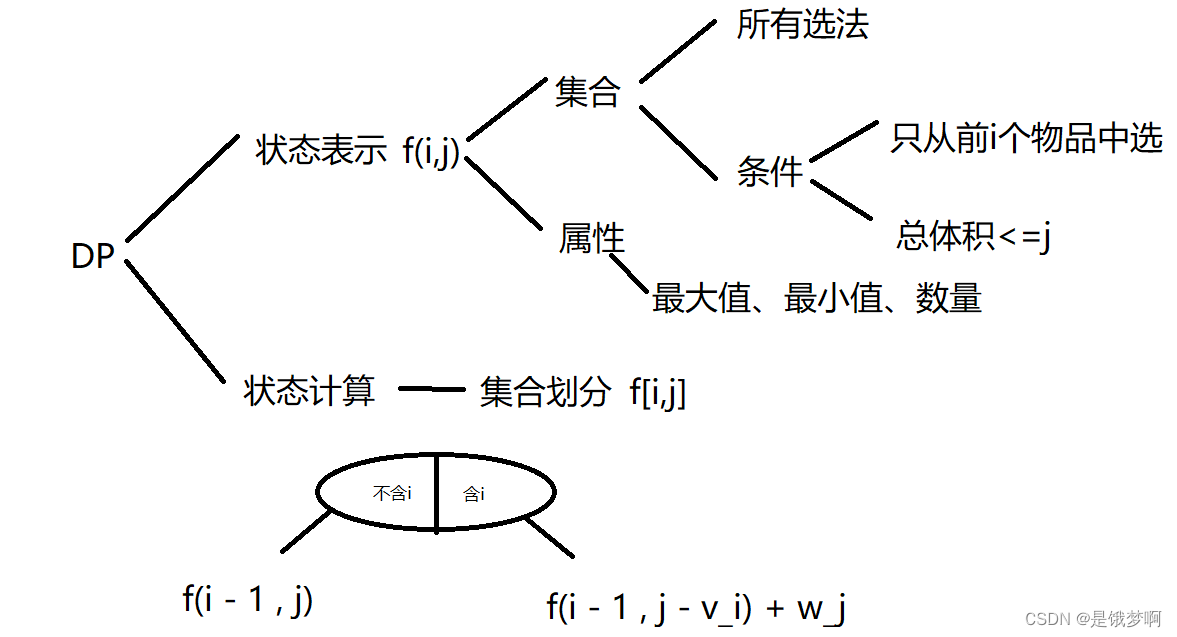

对于每个块黄金，我们都有两种选择，选或者不选。

在所有的选法中，对于第 i 块黄金，当我们不选择它时，f(i , j) = f ( i - 1 , j );

当我们选择它时，我们需要换一个思路考虑，在所有的选法中，我们都选择了这块黄金，我们在所有的选法中，都减去这个黄金的，也就是从前 i-1块黄金中选，总体积不超过j-v_{i},即f(i,j) = f(i-1,j-v_{i}) + w_{i};最后在加上第i块黄金的价值。

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 1010;

int n,m;

int f[N][N];

int t[N],w[N];


int main()
{
    
    scanf("%d%d",&m,&n);
    
    for(int i =1 ; i <=n ;i ++) scanf("%d%d",&t[i],&w[i]);
    
    
    for(int i = 1; i <= n ;i ++)
    {
        for(int j = 0 ; j<= m; j ++)
        {
            f[i][j] = f[i-1][j];
            if(j>=t[i]) f[i][j] = max(f[i][j],f[i-1][j-t[i]] + w[i]);
        }
    }
    printf("%d",f[n][m]);
    
    return 0;
}

现在我们来思考一下优化：

f(i,j)中对于第i层的更新，我们只用到了第i-1层，没有用到i-2及之前的数据。于是我们可以使用一维来存储，更新的时候直接更新掉就行，反正以后也用不到了。我们直接删掉第一维，考虑是否正确。

 
    for(int i = 1; i <= n ;i ++)
    {
        for(int j = t[i] ; j<= m; j ++)
        {
            f[j] = max(f[j],f[j-t[i]] + w[i]);
        }
    }

我们删掉第一维后，核心代码变成了这个样子，我们思考

f[j] =max(f[j],f[j-t_{i}]+w_{i})是否等价于f[i][j] =max(f[i][j],f[i-1][j-t_{i}]+w_{i})

答案是否定的，其应该等价于 f[i][j] =max(f[i][j],f[i][j-t_{i}]+w_{i})，当我们直接去掉第一维后，相当于所有的第一维都变成相同的了，但其实并不相同。

我们知道 j-t_{i}<j,我们更新 j 时其实用到的也只有i-1时的j-t_{i}。我们只要倒着遍历，这样，访问f[j-t_{i}]时，其值还没有被更新也就还是第i-1层的数据。

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 1010;

int n,m;

int f[N];

int t[N],w[N];


int main()
{
    
    scanf("%d%d",&m,&n);
    
    for(int i =1 ; i <=n ;i ++) scanf("%d%d",&t[i],&w[i]);
    
    for(int i = 1; i <= n ;i ++)
    {
        for(int j = m ; j>=t[i]; j --)
        {
            f[j] = max(f[j],f[j-t[i]] + w[i]);
        }
    }
    printf("%d",f[m]);
    
    return 0;
}

完全背包：

疯狂的采药 - 洛谷https://www.luogu.com.cn/problem/P1616

完全背包的背景：

完全背包和01背包的区别就在于，完全背包中，每个物品的数量都是无限的，可以取无限个，只要不超过背包容量。

闫式DP分析法：

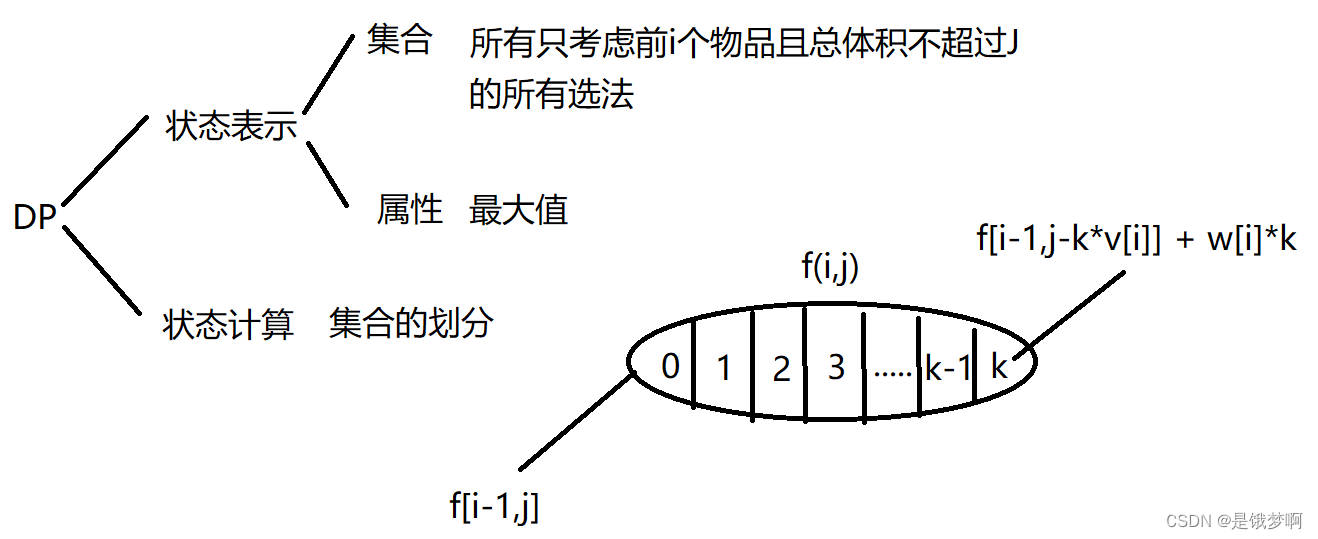
 此次集合划分中，我们根据每个物品选取的数量进行划分；

当我们选取0个物品时,也就是第i个物品一个也不选，即：f[i,j] = f[i-1,j]

当我们选取K个物品时，我们采取和之前01背包一样的解决策略，每个方案都选取了k个第i个物品，我们将所有方案都减去第i个物品，最后在加上第i个物品的价值，即：

f[i,j] = f[i-1,j-k*v[i]]+w[i]*k

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>

using namespace std;

typedef long long LL;
typedef pair<int,int> PII;

const int N = 1010;

int n,m;

int f[N][N];
int t[N],w[N];

int main()
{
	cin >> m >> n;
	
	for(int i =1 ;i <= n ;i ++) cin >> t[i] >> w[i];
	
	for(int i = 1 ;i <= n ;i ++)
	{
		for(int j =0 ;j <= m ;j ++)
		{
			for(int k = 0 ;k *t[i] <= j ; k ++)
			f[i][j] = max(f[i][j],f[i-1][j-k*t[i]]+w[i]*k);
		}
	}
	
	cout<<f[n][m];	
	
	
	return 0;
}

我们发现这个写法时间复杂度太高了，看看有没有优化的方法。

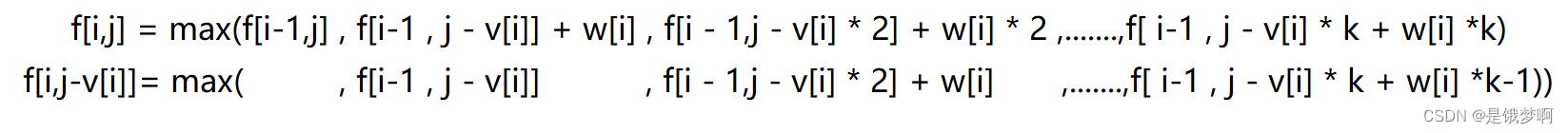
我们观察上式发现，f[i,j]和f[i,j-v[i]]的状态很像；

于是乎，我们的f[i,j]就可以利用f[i,j-v[i]]的状态进行优化，即

f[i,j] = max(f[i-1,j],f[i,j-v[i]]+w[i]); 

for(int i = 1 ;i <= n ;i ++)
	{
		for(int j =0 ;j <= m ;j ++)
		{
			f[i][j] = f[i-1][j];
			if(j>=t[i]) f[i][j] = max(f[i][j],f[i][j-t[i]]+w[i]);
		}
	}

接下来我们对比完全背包和01背包的状态转移方程：

01背包：f[i,j] = max(f[i-1,j],f[i-1,j-v[i]] +w[i]) 

完全背包：f[i,j] = max(f[i-1,j],f[i,j-v[i]]+w[i])

我们考虑将完全背包优化到一维(将第一维直接删掉)：

for(int i = 1 ;i <= n ;i ++)
	{
		for(int j =t[i] ;j <= m ;j ++)
		{
			f[j] = max(f[j],f[j-t[i]]+w[i]);
		}
	}

完全背包中，因为j-v[i]是第i层，所以没有01背包那个问题，可以直接删掉第一维。

//AC代码
#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>

using namespace std;

typedef long long LL;
typedef pair<int,int> PII;

const int N = 1e7+10;

int n,m;

LL f[N];
int t[N],w[N];

int main()
{
	scanf("%d%d",&m,&n);
	
	for(int i =1 ;i <= n ;i ++) scanf("%d%d",&t[i],&w[i]);
	
	for(int i = 1 ;i <= n ;i ++)
	{
		for(int j =t[i] ;j <= m ;j ++)
		{
			f[j] = max(f[j],f[j-t[i]]+w[i]);
		}
	}
	
	printf("%lld",f[m]);	
	
	return 0;
}

多重背包：

宝物筛选 - 洛谷https://www.luogu.com.cn/problem/P1776多重背包和完全背包的一个区别的，物品的数量不在是有无限个，而是有固定是s[i]个；

那我们完全背包的朴素版本和完全背包就很类似了；

 for(int i = 1 ;i <=n ;i ++)
    {
        for(int j = 0; j<= m ;j ++)
        {
            for(int k =0 ;k <= s[i] && k*v[i] <= j ; k ++)
            {
                f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+w[i]*k);
            }
        }
    }

这里我们只需要控制一下，每个物品可以选取的最大数量以及不要超过容量的上限即可。

但是这样的方法时间复杂度太高了，这是我们接受不了的。我们考虑有没有优化方式。

对于每个物品，我们考虑了选取1个、2个、..........等等。我们每次选取都做了很多重复性工作，我们考虑能不能将进行打包，以减少枚举次数。

这就是二进制分组优化方案：

举个例子：

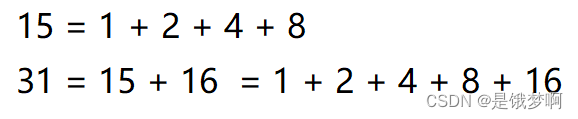
 也就是说任何一个+1后是2的整数次幂的数都可以通过二进制进行拆分。

那如果是一个随便的数是否也可以凑呢

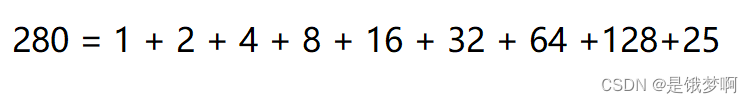
从1~128中，我们可以凑出1~255中的任何一个数，但是不够280；要是加上256就超出了280的范围。

我们最后加上280 - 255 = 25 的话，1~128可以凑出1~255中的任何一个数加上25，就可以凑出1~280中的任何一个数不重不漏。

时间复杂度就可以从O(N*M*S)优化到O(N*M*log(S));

//AC代码
#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>

using namespace std;


typedef long long LL;
typedef pair<int,int> PII;

const int N = 1000010;

int n,m;
int v[N],w[N];
int f[N];

int main()
{
	cin >> n >> m;
	
	int cnt = 0;
	for(int i = 1; i<= n; i++)
	{
		
		int a,b,c;
		cin >> a >> b >> c;
		
		int k = 1;
		while(k<= c)
		{
			cnt ++;
			v[cnt] = a * k;
			w[cnt] = b * k;
			c -= k;
			k *= 2;
		}
		if(c > 0)
		{
			cnt ++;
			v[cnt] = a * c;
			w[cnt] = b * c;
		}
	}
	
	n = cnt;
	
	for(int i =1 ;i <= n ;i ++)
	{
		for(int j = m ;j >= w[i] ;j --)
		{
			f[j] = max(f[j],f[j-w[i]]+v[i]);
		}
	}
	
	cout<<f[m]<<endl;
	
	return 0;
}

分组背包：

通天之分组背包 - 洛谷https://www.luogu.com.cn/problem/P1757

分组背包背景：

有 N 组物品和一个容量是 V 的背包。

每组物品有若干个，同一组内的物品最多只能选一个。
每件物品的体积是 v_{ij}，价值是w_{ij}，其中 i 是组号，j 是组内编号。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

闫式DP分析法：

 我们这次是遍历第 i 组中第 k 个物品选或不选，最后也就转化为了01背包问题；

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<vector>

using namespace std;

const int N = 10010,M = 110;
typedef long long LL;
typedef pair<int,int> PII;

int n,m;

vector<vector<int>> val,wei;
int cnt;
int st[N],f[N];

int main()
{
	cin >> m >> n;
		
	val.resize(M);
	wei.resize(M);
	
	for(int i =1;i <=n ;i ++)
	{
		int a,b,c;
		cin >> a >> b >> c;
		
		if(!st[c]) cnt++,st[c] = 1;
		
		wei[c].push_back(a);
		val[c].push_back(b);
	}
	
	for(int i = 1;i <= cnt ; i ++)
	{
		for(int j = m ;j >=0; j--)
		{
			for(int k = 0;k < wei[i].size() ;k ++ )
			if(wei[i][k]<=j) f[j] = max(f[j],f[j-wei[i][k]]+val[i][k]);
		}	
	}
	
	cout<<f[m]<<endl;
	
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/612229.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【Python】深度理解Class类、Object类、Type元类的概念和关系

【Python】深度理解Class类、Object类、Type元类的概念和关系

深度理解Class类、Object类、Type元类 1.Class类、Object类、Type元类的表面关系2.Class、Object、Type解释3.关系详解4.那么如何看待object、type在Python面对对象概念中的一席之地呢&#xff1f;5.那么object、type扮演了什么样的角色呢&#xff1f;他们对class又分别做了什么…
阅读更多...
【计算机组成】Cache与CPU的直接映射、全相联映射与组相联映射

【计算机组成】Cache与CPU的直接映射、全相联映射与组相联映射

一.Cache与CPU需要映射的原因 CPU准备访问内存时&#xff0c;会先问问cache存储器有没有已经提前准备好了数据&#xff0c;如果没有则再找内存要&#xff1a; 如果Cache刚好命中&#xff0c;则直接从Cache中读取数据&#xff1a; 如果Cache没有命中&#xff08;Cache失效&#…
阅读更多...
时序数据库InfluxDB快速入门使用

时序数据库InfluxDB快速入门使用

推荐博客&#xff1a; Influxdb中文文档 linux安装influxdb Influxdb安装、启动influxdb控制台、常用命令、Influx命令使用、Influx-sql使用举例、Influxdb的数据格式、Influxdb客户端工具 1.安装 1、influxdb数据库官网的下载链接&#xff1a; https://portal.influxdata.c…
阅读更多...
如何利用MES系统进行生产防呆防错？

如何利用MES系统进行生产防呆防错？

一、认识MES系统的防呆防错功能 首先&#xff0c;我们要清楚了解&#xff0c;什么是MES系统的防呆防错。MES系统防呆防错是指利用MES系统来避免生产过程中的错误和缺陷&#xff0c;保障生产排程和生产过程顺利进行的过程。MES系统防呆防错包括以下方面&#xff1a; 1. 自动识别…
阅读更多...
relation-graph关系图谱组件2.0版本遇到的问题

relation-graph关系图谱组件2.0版本遇到的问题

前提&#xff1a;之前已经写过一篇1.1版本的问题&#xff0c;这里就不过多讲了&#xff08;如果想要解决火狐低版本兼容&#xff0c;看那个就行&#xff09; 这次主要讲的是和1.X版本的区别和一些其它问题 区别 参数名不同&#xff1a;以前的links>lines (虽然现在links也…
阅读更多...
遇见未来，降低职场焦虑——中国人民大学与加拿大女王大学金融硕士来助力

遇见未来，降低职场焦虑——中国人民大学与加拿大女王大学金融硕士来助力

身在职场的你有感到一丝丝的焦虑吗&#xff1f;偶尔的小焦虑可以作为我们工作中的动力&#xff0c;时刻提醒我们保持奋进。预见未来才能遇见未来&#xff0c;随着社会经济不断发展&#xff0c;没有什么是一成不变的。处于职场上升期的我们更要懂得未雨绸缪&#xff0c;增加自身…
阅读更多...
ClickHouse集群搭建总结

ClickHouse集群搭建总结

简介 ClickHouse是俄罗斯最大的搜素引擎Yandex于2016年开源的列式数据库管理系统&#xff0c;使用C 语言编写, 主要应用于OLAP场景。 使用理由 在大数据量的情况下&#xff0c;能以很低的延迟返回查询结果。 笔者注&#xff1a; 在单机亿级数据量的场景下可以达到毫秒级的查询…
阅读更多...
SpringCloudAlibaba 微服务生态

SpringCloudAlibaba 微服务生态

一 微服务架构 1.1 微服务 微服务其实是一种架构风格&#xff0c;我们在开发一个应用的时候这个应用应该是由一组小型服务组成&#xff0c;每个小型服务都运行在自己的进程内&#xff1b;小服务之间通过HTTP的方式进行互联互通。 1.2 微服务架构的常见问题 一旦采用微服务系…
阅读更多...
ChatGPT 之后，B 端产品设计会迎来颠覆式革命吗？| Liga妙谈

ChatGPT 之后，B 端产品设计会迎来颠覆式革命吗？| Liga妙谈

近日&#xff0c;脑机接口公司 Neuralink 宣布&#xff0c;其植入式脑机接口设备首次人体临床研究已被准许启动。遥想当年&#xff0c;我们还嘲讽罗老师「动嘴做 PPT」&#xff0c;谁曾想不久后我们可能连嘴都不用动&#x1f64a;。 脑机接口何时会引爆人机交互革命尚未可知&a…
阅读更多...
简述三观；

简述三观；

文章目录 三观世界观人生观价值观三观不合怎么看三观不正: 教养育儿教育心智不成熟的表现 三观 指人生观&#xff0c;世界观和价值观; https://wenku.baidu.com/view/102a655fd4bbfd0a79563c1ec5da50e2534dd1d8.html?fraladdin664466&ind1&_wkts_1685949448098&…
阅读更多...
深入理解API网关Kong：动态负载均衡配置

深入理解API网关Kong：动态负载均衡配置

深入理解API网关Kong&#xff1a;动态负载均衡配置 背景 在 NGINX 中&#xff0c;负载均衡的配置主要在 upstream 指令中进行。upstream 指令用于定义一个服务器群组和负载均衡方法。客户端请求在这个服务器群组中进行分发。 NGINX 提供了以下几种负载均衡方法&#xff1a; …
阅读更多...
python接口自动化 —— 什么是接口、接口优势、类型（详解）

python接口自动化 —— 什么是接口、接口优势、类型（详解）

简介 经常听别人说接口测试&#xff0c;接口测试自动化&#xff0c;但是你对接口&#xff0c;有多少了解和认识&#xff0c;知道什么是接口吗&#xff1f;它是用来做什么的&#xff0c;测试时候要注意什么&#xff1f;坦白的说&#xff0c;笔者之前也不是很清楚。接下来先看一下…
阅读更多...
从简历被拒到收割 8 个高薪 offer，我用了 3 个月...

从简历被拒到收割 8 个高薪 offer，我用了 3 个月...

半年前我一个小老弟从外包离职了&#xff0c;本以为有两年经验进个一般的公司没有问题的&#xff0c;结果人家一看是外包出来的&#xff0c;面试问的问题也不是很懂&#xff0c;简历被拒了好几次。还好这个小老弟没有气馁&#xff0c;在论坛博客和里面的大佬虚心学习&#xff0…
阅读更多...
地震勘探基础（八）之地震动校正

地震勘探基础（八）之地震动校正

地震动校正 在地震资料数字处理过程中&#xff0c;速度分析&#xff0c;动校正和水平叠加三个处理内容是相互关联的。水平叠加是为了提高地震资料的信噪比&#xff0c;要想得到好的叠加效果&#xff0c;必须做好动校正。而做好动校正&#xff0c;需要进行准确的速度分析。只有…
阅读更多...
Tomcat部署

Tomcat部署

目录 Tomcat 什么是 servlet&#xff1f; 什么是 JSP? Tomcat 功能组件结构&#xff1a; Container 结构分析&#xff1a; Tomcat 请求过程&#xff1a; ---------------------Tomcat 服务部署------------------------- 1.关闭防火墙&#xff0c;将安装 Tomcat 所需软…
阅读更多...
长尾词挖掘，长尾词的优化方法有哪些

长尾词挖掘，长尾词的优化方法有哪些

我们都知道&#xff0c;长尾词能给我们带来较高的流量和转化率&#xff0c;且优化难度低&#xff0c;成本低。今天就来分享长尾词的优化方法。 首先需要挖掘长尾词&#xff0c;挖掘长尾词的方法以下3种比较实用&#xff1a; 1、使用长尾词挖掘工具 可以通过第三方工…
阅读更多...
ROS：tf坐标系广播与监听的编程实现

ROS：tf坐标系广播与监听的编程实现

目录 一、创建功能包二、创建代码并编译运行&#xff08;C&#xff09;2.1创建代码2.2编译2.3运行 一、创建功能包 创建的 learning_tf 包来进行代码存放和编译 cd ~/catkin_ws/src catkin_create_pkg learning_tf roscpp rospy tf turtlesim二、创建代码并编译运行&#xff…
阅读更多...
银行业务相关

银行业务相关

省联社&#xff0c;农商行、农村信用社之间的关系 一些知乎回答 省联社、农商行、农村信用社之间有什么联系&#xff1f; - mobye的回答 - 知乎 https://www.zhihu.com/question/24220844/answer/28276903 发源于空想社会主义&#xff0c;世界上第一个信用合作社诞生于1984年的…
阅读更多...
第9章集 合

第9章集 合

文章目录 9.1 Java集合框架9.1.1 集合接口与实现分离9.1.3 迭代器9.1.4 泛型实用方法 9.2 集合框架中的接口9.3.1 链表9.3.2 数组列表9.3.3散列集9.3.4 树集9.3.5 队列与双端队列9.3.6 优先队列 9.4 映射9.4.1 基本映射操作9.4.2 更新映射条目9.4.3 映射视图9.4.4 弱散列映射9.…
阅读更多...
python数据可视化-matplotlib学习总结

python数据可视化-matplotlib学习总结

目录 &#xff08;一&#xff09;常见的图形 1、趋势图&#xff08;直线图&#xff09;&#xff1a;plot&#xff08;&#xff09; 2、散点图&#xff1a;scatter(): (二&#xff09;统计图形 1、柱状图&#xff1a;bar( 2、条形图&#xff1a;barh() 3、直方图&#xff…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023