图的连通度
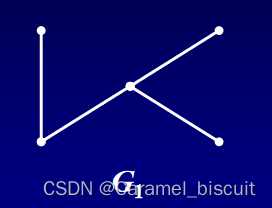
删去任意一条边后便不连通
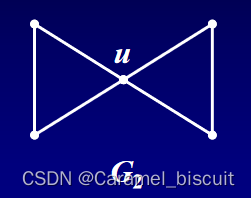
删去任意一条边后仍连通,但删去点u后不连通。

G3和G4删去任意一条边或任意一个点后仍连通,但从直观上看,G4的连通程度比G3高。
割边
设e是图G的一条边,若ω(G-e)>ω(G),则称e为G的割边。——若删去一条边,使图的分枝数变大,则称为割边。
若G连通,则割边是指删去后使G不连通的边,故非平凡树的每条边都是割边。
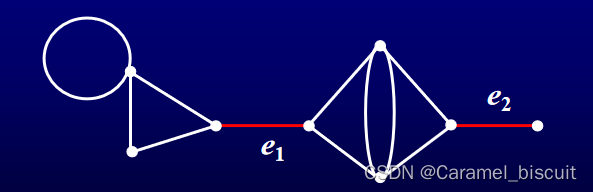
图中,边e1和e2为割边,而其余边均不为割边。
定理:e是图的割边当且仅当e不在G的任何圈中。
证明:因结论若在G的含e的连通分支中成立,则必在G中成立,所以我们不妨假定G连通。
必要性:设e=uv是图的割边,若e在圈C中,令P=C-e。
易知P是G-e中一条(u,v)路。
任取G-e中两个不同点x和y,因G连通,故G中存在(x,y)路Γ。
若Γ不含e,作为Γ是G-e中一条(x,y)路。
若Γ含e,用P替换e后也可以得到G-e中一条(x,y)路,以上表明G-e连通,这与e是割边矛盾,所以e不在G的任何圈中。
充分性:设e=uv,若e不是G的割边,则G-e仍连通,从而G-e中存在(u,v)路P,这样P+e便是G中含e的圈,这与假设“e不在G的任何圈中”矛盾。
圈中的边一定不是割边,所以删去圈中的边不会破坏图的连通性。
设e是连通图G的任意一条边,若e含在G的某圈中,则G-e仍连通。
若G的每个顶点的度数均为偶数,则G没有割边。
若不然,设e=uv为割边,则G-e的含有顶点u(或v)的那个分支中点u或v的度数必为奇数,而其余点的度数均为偶数,与度数为奇数的顶点的个数为偶数矛盾。
若G为k正则二部图,则G无割边。
若不然,设e=uv为G的割边。
假设G1为G-e的包含顶点u的连通分支,显然G1中除了点u的度数为k-1,其余点的度数均为k。
显然G1仍然为偶数,设其二部划分为S和T,且|S|=s,|T|=t。
不妨假设S包含顶点u,则ks-1=|E(G1)|=kt.
但是因为k≥2,所以等式不能成立,因此e一定不是割边。
割点及其性质
定义:图G=(V,E)的顶点v称为割点,如果E可划分为两个非空子集E1和E2,使得G[E1]和G[E2]恰有一个公共顶点v。
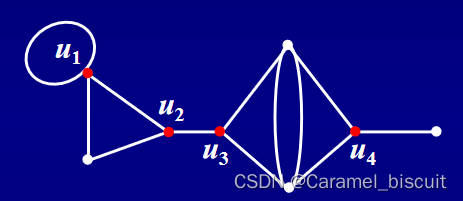
图中u1,u2,u3和u4是割点,其余点均不为割点。
- 若ω(G-v)>ω(G),则v必为G的割点。
- 若G无环,则v是G的割点当且仅当ω(G-v)>ω(G)。
- 若无环图G连通,则割点是指删去该点使G不连通的点。