摘要

This week, I read a computer science about GNN. At present, the attention mechanism of graph neural network is not well understood, especially the graph noise problem. In this paper, self-supervised graph attention Network is proposed, which is an improved noise graph attention model. Specifically, edges are predicted using two forms of attention compatible with self-supervised tasks, whose presence and absence contain inherent information about the importance of the relationship between nodes. By encoding the edges, SuperGAT gains more attention when it comes to distinguishing errant chain neighbors. Experiments on real data sets show that the performance of the designed model is significantly better than that of the most advanced baseline. In addition, I learn the weighted residual value method of finite element, realize the shortest circuit algorithm with python, and learn and think about the principle of Gaussian diffusion equation.

本周，阅读了一篇与GNN相关的文章。目前，大家对图神经网络的注意力机制还没有很好地理解，特别是图噪声问题。对此，提出了自监督图注意网络(SuperGAT)，即一种改进的噪声图注意力模型。具体来说，利用与自监督任务兼容的两种注意力形式来预测边缘，其存在和不存在包含了节点之间关系重要性的固有信息。通过对边缘进行编码，SuperGAT在区分错链邻居时获得了更多的注意力。通过在真实数据集上的实验表明，所设计模型的性能明显优于最先进的基线。此外，我学习了有限元的加权残值法内容，用python实现最短路算法以及学习并思考了高斯扩散方程的原理内容。

文献阅读

1.题目

文献链接：How to Find Your Friendly Neighborhood: Graph Attention Design with Self-Supervision

2.背景

最近，图神经网络通过聚合其邻居节点的特征来生成中心节点的特征，从而显示出显著的性能提升。然而，现实世界的图通常是有噪声的，不相关节点之间的连接（节点之间的类别不同），阻碍了GNN模型的性能。图注意力网络(GATs) ，采用自注意力机制来缓解这个问题。类似于序列数据中的注意力，图注意力捕获了图的关系重要性。换句话说，每个邻居对表示中心节点的重要性程度。GATs在节点分类方面表现出了性能的提高，但它们在不同数据集中改进的程度不一致，而且对图注意力实际学习的内容很少。

3.方案

根据明确的分析，提出了SuperGAT的两种变体：scaled dot- product (SD)和mixed GO and DP (MX)，以强调GO和DP的优势。这两种图注意力关系重要性取决于图的平均度和同质性，因此生成具有不同度和同质性的合成图数据集，并分析注意力的选择对节点分类性能的影响。基于这个结果，提出了一种具有边自监督的图注意力的方法，该方法对给定的图特征最有效。在17个真实数据集上进行了实验，并表明所提出的方法可以在这些数据集上进行推广，所提出的模型性能优于基线。

4.本文贡献

1）提出了利用边信息的自监督注意力模型；
2）使用标签一致性和链接预测任务对经典的注意力形式GO和DP进行分析，发现GO在标签一致性和DP在链接预测方面表现更好；
3）提出了基于同质性和平均度的图注意力设计方法，并通过在真实数据集上的实验验证了其有效性。

5.模型

5.1 图注意力形式

在两种广泛使用的注意力机制中，原始的GAT (GO)通过以 al+1 ∈ R2^Fl+1为参数的单层前馈网络来计算系数。另一个是点积(DP)注意力，受到之前关于节点表示学习的工作的启发，它采用了相同的数学表达式用于链路预测得分。本文进一步扩展了注意力机制，除了层注意力（GO），提出了点积（DP）注意力，形式如下：
在这里插入图片描述

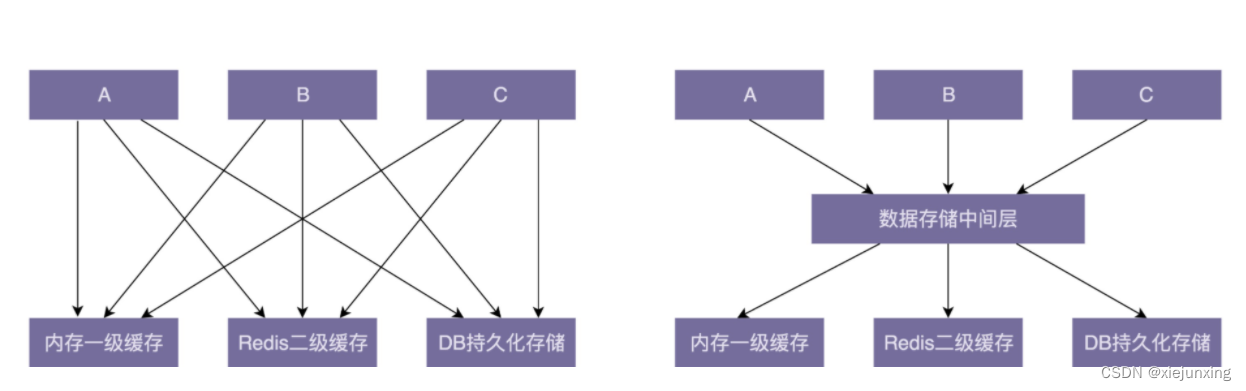
5.2 superGAT

提出了用节点对之间的边的存在或不存在来引导注意力的模型–SuperGAT。利用链接预测任务使用来自边的标签来自我监督注意力：对于一对 i 和 j，如果存在边，则为1，否则为0。引入带 aφ 和sigmoid函数σ，推导出 i 和 j 之间一条边的概率φij：
在这里插入图片描述
基于GO和DP注意力，采用了四种SuperGAT类型(GO、DP、SD和MX)。对于更高级的版本，用 i 和 j 之间存在边的非归一化注意力 eij 和概率 φij 来描述 SuperGATSD和SuperGATMX：

SuperGATSD将节点的点积除以一个维度的平方根，这可以防止一些较大的值在softmax后主导整个注意力。 SuperGATMX用sigmoid乘GO和DP注意，这种形式的动机来自于门控循环单元的门控机制。由于DP注意力的sigmoid表示边的概率，它可以轻轻地删除不太可能链接的邻居，同时隐式地分配其余节点的重要性。

将层 l 的优化目标定义为二元交叉熵损失：
在这里插入图片描述
其中：1是指标函数，在每次训练迭代中，从随机性中获得正则化效果。最后，我们结合了节点标签上的交叉熵损失、所有 L 层的自监督图注意损失和L2正则化损失，混合系数为 λE 和 λ2：

下图中虚线框中的部分代表了原始的GAT模型（单层）：
在这里插入图片描述

6.实验

在多个真实数据集上，SuperGAT都得到了更好的结果。
在这里插入图片描述

7.结论

1）根据输入图的特征，提出了一种新的图神经结构设计来自监督图的注意力。
2）首先评估了什么是图注意学习，并分析了边缘自我监督对链接预测和节点分类性能的影响。
3）通过分析表明，两种广泛应用的注意力机制(原始GAT和点积)在同时编码标签一致性和边缘存在性方面存在困难。
4）针对这一问题，提出了几种平衡这两种因素的图注意形式，并认为应该根据输入图的平均度和同质性来设计图注意。
5）实验结果证明，图形注意力可以在各种真实世界的数据集上推广，因此设计出的模型优于其他基线模型。

有限元

通过上周对加权残值法的学习，现在我们知道试函数高度够了，怎样才能让它更加贴近真实解，所以再引入一个自由度：
在这里插入图片描述
因此两个方程，两个未知数，可以求解，引入两个自由度就如此贴近真实值：

再来看得到的近似解在 (0, 1) 各处的残差，有：

如下图所示，取的试函数越多，残差就会越小，因此我们需要有序且密集地分布的试函数：
在这里插入图片描述

数学建模

python实现最短路径算法：

import numpy as np


# 找到一条从start到end的路径
def findPath(graph, start, end, path=[]):
    path = path + [start]
    if start == end:
        return path
    for node in graph[start]:
        if node not in path:
            newpath = findPath(graph, node, end, path)
            if newpath:
                return newpath
    return None


# 找到所有从start到end的路径
def findAllPath(graph, start, end, path=[]):
    path = path + [start]
    if start == end:
        return [path]

    paths = []  # 存储所有路径
    for node in graph[start]:
        if node not in path:
            newpaths = findAllPath(graph, node, end, path)
            for newpath in newpaths:
                paths.append(newpath)
    return paths


# 查找最短路径
def findShortestPath(graph, start, end, path=[]):
    path = path + [start]
    if start == end:
        return path

    shortestPath = []
    for node in graph[start]:
        if node not in path:
            newpath = findShortestPath(graph, node, end, path)
            if newpath:
                if not shortestPath or len(newpath) < len(shortestPath):
                    shortestPath = newpath
    return shortestPath


# 以字典的形式构建有向图
graph = {'A': ['B', 'C', 'D'],
         'B': ['E'],
         'C': ['D', 'F'],
         'D': ['B', 'E', 'G'],
         'E': [],
         'F': ['D', 'G'],
         'G': ['E']}

onepath = findPath(graph, 'A', 'G')
print('一条路径:', onepath)

allpath = findAllPath(graph, 'A', 'G')
print('\n所有路径：', allpath)

shortpath = findShortestPath(graph, 'A', 'G')
print('\n最短路径：', shortpath)

查看程序输出：

一条路径: ['A', 'C', 'D', 'G']

所有路径： [['A', 'C', 'D', 'G'], ['A', 'C', 'F', 'D', 'G'], ['A', 'C', 'F', 'G'], ['A', 'D', 'G']]

最短路径： ['A', 'D', 'G']

深度学习

1.高斯扩散

高斯扩散是一种常用的大气污染物传输模型，基于高斯分布原理，可以用于描述大气中污染物的传播和扩散过程。该模型假设大气中的污染物传输是在平稳、均匀的大气环境条件下进行的。

2.原理

1）高斯分布，也称为正态分布，是一种常见的连续概率分布。它的特点是在分布的中心具有一个峰值，两侧呈对称的形状。高斯分布的概率密度函数可以用以下公式表示：
在这里插入图片描述
其中，μ是均值，σ是标准差，x是变量。
2）根据高斯分布的特性，可以将大气中污染物的传输过程近似为高斯扩散过程。假设污染物的源释放在某一点上，根据风向和风速等大气运动参数，可以计算出不同位置处的污染物浓度。根据高斯扩散模型，离源点越远的位置，污染物浓度逐渐减小，呈现出高斯分布的形状。
3）高斯扩散模型中的关键参数是扩散系数，它描述了污染物在大气中的传输和扩散速度。扩散系数受到风速、大气稳定度等因素的影响。一般来说，风速越大、大气稳定度越差，污染物传输的速度越快，扩散范围越广。
4）高斯扩散模型基于一些简化假设，例如，假设大气环境是均匀的、平稳的，并且污染物的源释放是稳定的。实际情况中，大气环境具有复杂的非均匀性和动态性，还会受到地形、建筑物等因素的影响。因此，高斯扩散模型在复杂的大气环境中的应用存在一定的限制。

总结

通过本周对有限元中加权残值法的补充学习，我体会到有限元的本质就是系统化地定义试验函数T和试函数以高效地求解试验函数中的未知系数。在有限元中，有限元网格就提供了一个高效且系统化建立试函数和试验函数的方法。此外，还补充学习了高斯扩散的原理内容，以及用python实现最短路径算法。下周，我将继续思考论文的大致思路，争取有所突破。