OJ须知:
- 一般而言,OJ在1s内能接受的算法时间复杂度:10e8 ~ 10e9之间(中值5*10e8)。在竞赛中,一般认为计算机1秒能执行 5*10e8 次计算。
时间复杂度 取值范围 o(log2n) 大的离谱 O(n) 10e8 O(nlog(n)) 10e6 O(nsqrt(n))) 10e5 O(n^2) 5000 O(n^3) 300 O(2^n) 25 O(3^n) 15 O(n!) 11
时间复杂度排序:o(1) < o(log2n) < o(n) < o(nlog2n) < o(n^2) < o(n^3) < o(2^n) < o(2^n) < o(3^n) < o(n!)
目录
算法思想
算法局限性
过程
案例
平衡分割字符串⭐
方法一:贪心
复杂度分析
买股票的最佳时机2⭐⭐
方法一:贪心
复杂度分析
跳跃游戏⭐⭐
方法一:贪心(nums[i] == 0为核心)
复杂度分析
方法二:贪心(nums[i]为核心)
算法思想
贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的是在某种意义上的局部最优解。
融汇贯通的理解:
贪心算法是不会考虑全局的,其每一步都会确定当前其所看到的场景下的最优的一个解 —— 整个贪心问题的解:每一步的最优解叠加之后的结果。
有一个概念,就叫做最优子结构:每一个子问题,其的最优解最终叠加之后,能够作为最终问题的解,那就是最优子结构。
融汇贯通的理解:
所以,如果想用贪心算法,首先就要去确定一下,这个问题是不是最优子结构。(将问题进行一定的缩小,查看缩小版是否符合最优子结构)
算法局限性
用贪心算法的时候,其如果不是一个最优子结构,那我们得到的这一个解,其不一定是全局的一个最优解,有可能是一个局部的最优解。
- 不能保证求得的最后解是最佳的
- 不能用来求最大值或最小值的问题
- 只能求满足某些约束条件的可行解的范围比
过程
- 建立数学模型来描述问题
- 把求解的问题分成若干个子问题
- 对每一子问题求解,得到子问题的局部最优解
- 把子问题的局部最优解合成原来解问题的一个解
说白了就是:假设一个问题比较复杂,暂时找不到全局最优解,那么我们可以考虑把原问题拆成几个小问题(分而治之的思想),分别求每个小问题的最优解,再把这些 “局部最优解” 叠起来,就 “当作” 整个问题的最优解了。
案例
在我们排序所学知识中,选择排序就很好的诠释了贪心算法的使用。
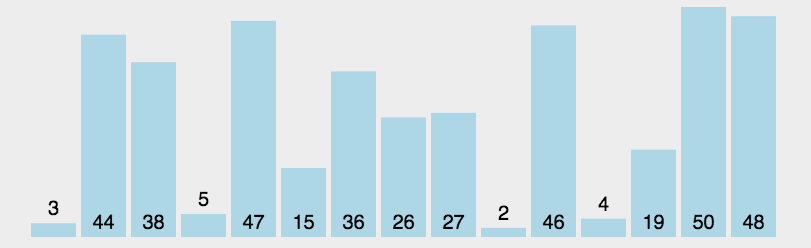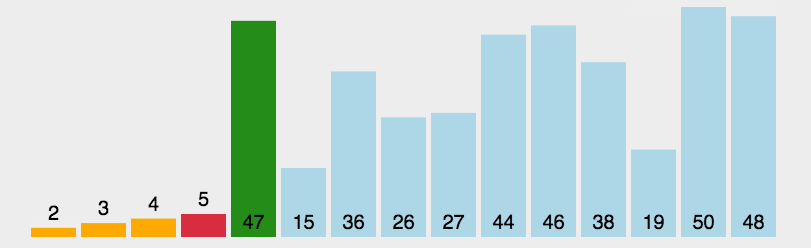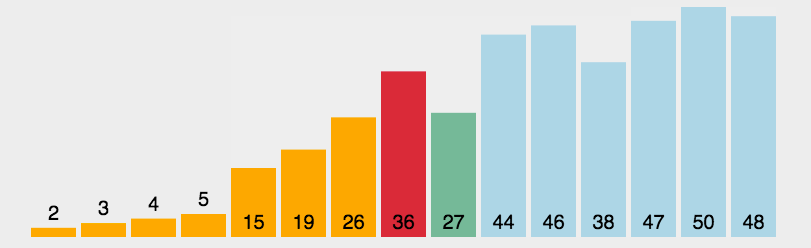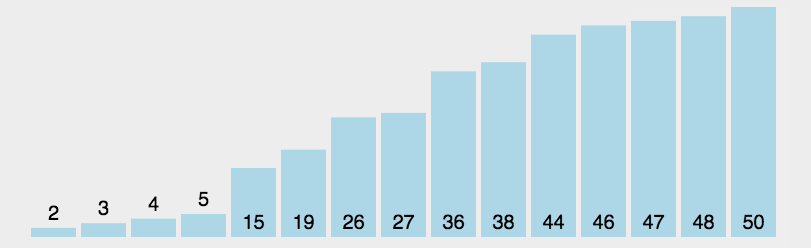
其每一次的排序都是选择未排序的区间内的最小值。 所以这个地方每一个子问题,其的最优解最终叠加之后,能够作为最终问题的解,所以是一个最优子结构。
//直接插入排序
// 对比 插入排序,谁更小。
void SelectSort(int* a, int n)
{
assert(a);
int begin_i = 0, end_i = n - 1;
while (begin_i < end_i)
{
// 贪心算法: 每次从未排序数组中找到最小值
int min_i = begin_i;
for (int i = begin_i + 1; i <= end_i; ++i)
{
if (a[i] < a[min_i])
min_i = i;
}
Swap(&a[begin_i], &a[min_i]);
++begin_i;
}
}贪心算法:每次找当前情况的最优解,不用考虑上一步是什么 / 下一步是什么。
平衡分割字符串⭐
1221. 分割平衡字符串 - 力扣(LeetCode)
平衡字符串 中,'L' 和 'R' 字符的数量是相同的。
给你一个平衡字符串 s,请你将它分割成尽可能多的子字符串,并满足:
每个子字符串都是平衡字符串。
返回可以通过分割得到的平衡字符串的 最大数量 。提示:
2 <= s.length <= 1000s[i] = 'L' 或 'R's是一个 平衡 字符串
方法一:贪心
抽象题中线索:
- 整体策略:不能让平衡字符串嵌套
- 当前情况决策:当前情况下的字符串,是否符合平衡分割字符串
class Solution {
public:
int balancedStringSplit(string s) {
int ret = 0;
int balance = 0;
for(auto ch : s)
{
// 当前情况决策: 当前情况下的字符串,是否符合平衡分割字符串
ch == 'L' ? balance++ : balance--;
if(balance == 0) ret++;
}
return ret;
}
};复杂度分析
- 时间复杂度:O(n)。
- 空间复杂度:O(1)。
买股票的最佳时机2⭐⭐
122. 买卖股票的最佳时机 II
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你
也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
提示:
1 <= prices.length <= 3 * 10e40 <= prices[i] <= 104
方法一:贪心
抽象题中线索:
- 整体策略:不能股票的购买售出嵌套
- 当前情况决策:当前情况下的股票以最低价买入,然后以高价售出
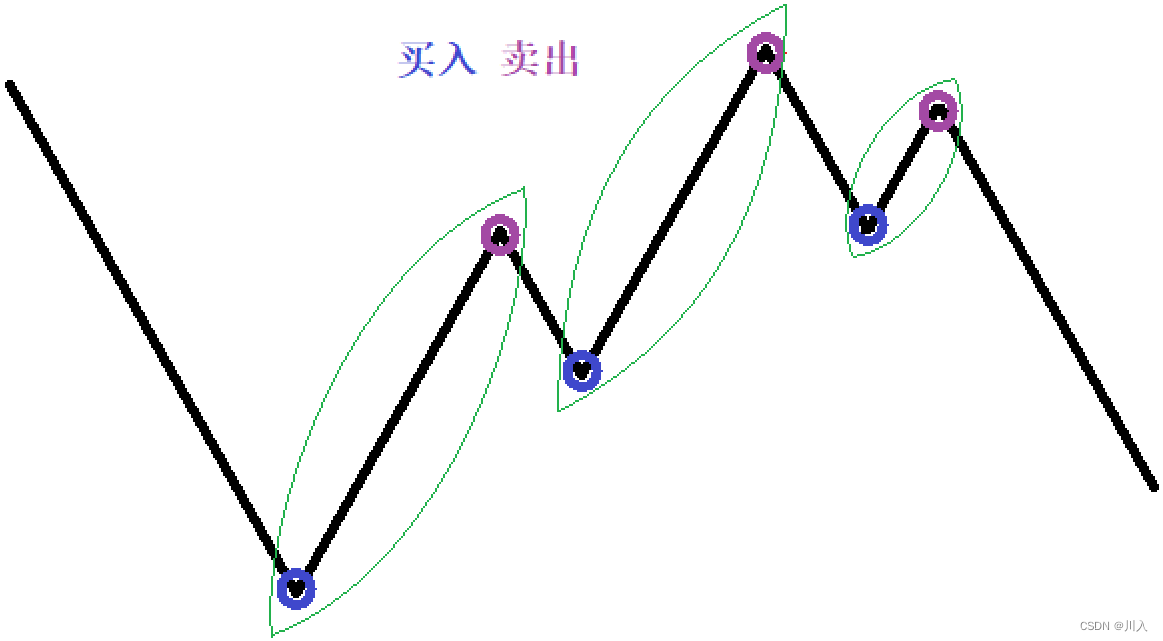
就是判断趋势:
- 连续上涨:上涨的最低点买入,上涨的最高点卖出 —— 上涨区间中买卖绝对利润相同。
- 连续下跌:不进行买卖。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int profit = 0;
int buy = prices[0];
int sell = 0;
for(int i = 1; i < prices.size(); i++)
{
// 判断趋势
if(prices[i] > prices[i - 1]) profit += prices[i] - prices[i - 1];
}
return profit;
}
};复杂度分析
- 时间复杂度:O(n)。
- 空间复杂度:O(1)。
跳跃游戏⭐⭐
55. 跳跃游戏 - 力扣(LeetCode)
给定一个非负整数数组
nums,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
提示:
1 <= nums.length <= 3 * 10e40 <= nums[i] <= 105
方法一:贪心(nums[i] == 0为核心)
抽象题中线索:
- 整体策略:不要嵌套nums[i] == 0。
- 当前情况决策:当前情况下有nums[i] == 0,其前面的最大值是否跨的过。
需要注意:最后一个数据为0,不用提出,已经到最后了。
class Solution {
public:
bool canJump(vector<int>& nums) {
int max = 0;
for(int i = 0; i < nums.size() - 1; i++)
{
// 当前情况决策: 当前情况下有nums[i] == 0,其前面的最大值是否跨的过
if(nums[i] + i > max) max = nums[i] + i;
if(nums[i] == 0)
if(max > i)
continue;
else
return false;
}
return true;
}
};max_i 位置很有可能已经完全足够到达最后,所以我们可以增加以一次判断。
class Solution {
public:
bool canJump(vector<int>& nums) {
int max_i = 0;
for(int i = 0; i < nums.size() - 1; i++)
{
// 当前情况决策: 当前情况下有nums[i] == 0,其前面的最大值是否跨的过
if(nums[i] + i > max_i)
if((max_i = nums[i] + i) >= nums.size() - 1) return true;
if(nums[i] == 0)
if(max_i > i)
continue;
else
return false;
}
return true;
}
};复杂度分析
- 时间复杂度:O(n)。
- 空间复杂度:O(1)。
方法二:贪心(nums[i]为核心)
抽象题中线索:
- 整体策略:不要嵌套nums[i + 1]。
- 当前情况决策:当前位置 i 前述最大值是否可以到达。
class Solution {
public:
bool canJump(vector<int>& nums) {
int max_i = 0;
for(int i = 0; i < nums.size(); i++)
{
// 当前情况决策: 当前位置 i 前述最大值是否可以到达。
if(max_i >= i)
{
max_i = max(max_i, nums[i] + i);
// max_i 位置已经完全足够到达最后
if(max_i >= nums.size() - 1) return true;
}
else return false;
}
return true;
}
};