随机森林入门

决策树入门、sklearn实现、原理解读和算法分析中针对决策树进行了详细的描述，但是其只考虑了一颗决策树的情况。俗话说，三个臭皮匠，顶个诸葛亮。本文将研究如何通过组合多颗决策树的方式，进一步提升模型的效果，即随机森林。

为了理解清楚随机森林算法背后的原理，我们先来看一个非常简单但却很有意思的实例：有3位法官需要判断被告是否有罪，最终的判断结果使用少数服从多数的方式确定。

假设每位法官判断正确的概率均为$p$，如果只有1位法官，那么该法官判断正确的概率就是$p$。

当法官数量增加至3位时，最终能够判断正确的情况有两种：一种是3位法官均判断正确，另一种是只有一位法官判断错误，其余两位则判断正确。其总概率为
$$p^3+3p^2(1-p)$$

只有3位法官判断正确的概率高于1位法官判断正确的概率时，增加法官数量才是有意义的，此时
$$p^3+3p^2(1-p)>p$$
化简得到
$$p(p-1)(p-0.5)<0$$
因为$p$的基本约束是$0\le p\le 1$，结合上式可以将约束条件变为
$$0.5<p<1$$

也就是说，只要单位法官判断正确的概率超过0.5，那么增加法官数量后，就可以进一步提升判断正确的概率。

除了概率约束，上述推导过程中还隐含了另外两个约束：（1）法官们各自做独立判断，互不影响，这是计算3位法官判断正确的概率的基本前提；（2）法官对表决对象拥有共同目标，因为如果有法官有意包庇罪犯，可能会故意给出错误判断。

事实上，已经有一个定理针对该情况进行了描述，即孔多塞陪审团定理：总数为奇数的一组人（模型）将未知的世界状态分为真或假。每个人（模型）正确分类的概率为$p>0.5$，并且任何一个人（模型）分类正确的概率在统计上独立于其他人（模型）分类的正确性。定理便可以描述为：多数投票正确的概率比任何人（模型）都更高；当人数（模型数）变得足够大时，多数投票的准确率将接近100%。

构造随机森林

将孔多塞陪审团定理应用到随机森林算法中：只要多颗树是相互独立的，并且每棵树预测正确的概率超过0.5，那么随机森林算法的效果就能优于单颗决策树。

单颗决策树预测正确的概率超过0.5大概率是正确的，因为随机猜测的正确概率已经是0.5，有了训练集的学习后，可以预期其判断正确的概率超过0.5。

实现多棵树为互相独立的方式是:
(1) 通过自助采样(bootstrap sample)策略生成不同且相互独立的数据集。其具体流程如下:从原数据集中有放回地（即同一样本可以被多次抽取）重复随机抽取一个样本，抽取次数与原数据集数量相同，这样会创建一个与原数据集大小相同的数据集，但有些数据点会缺失（缺失量大约37%），有些会重复。
(2) 基于新创建的数据集来构造决策树，但是要对我们在介绍决策树时所描述的算法稍作修改。在每个结点处，算法随机选择特征的一个子集，并对其中一个特征寻找最佳测试，而不是对每个结点都寻找最佳测试。选择的特征个数由max_features参数来控制。每个结点中特征子集的选择是相互独立的，这样树的每个结点可以使用特征的不同子集来做出决策。

由于使用了自助采样，随机森林中构造每棵决策树的数据集都是略有不同的。由于每个结点的特征选择，每棵树中的每次划分都是基于特征的不同子集。这两个步骤共同保证了随机森林中的所有树都不相同并且互相独立。

想要利用随机森林进行预测，首先需要对森林中的每棵树进行预测。此后，对于回归问题，我们对这些结果取平均值作为最终预测。对于分类问题，则采用“软投票”(soft voting)策略。也就是说，每个算法做出“软”预测，给出每个可能的输出标签的概率，对所有树的预测概率取平均值，然后将概率最大的类别作为预测结果。

以下为使用随机森林求解预测问题时的流程图。

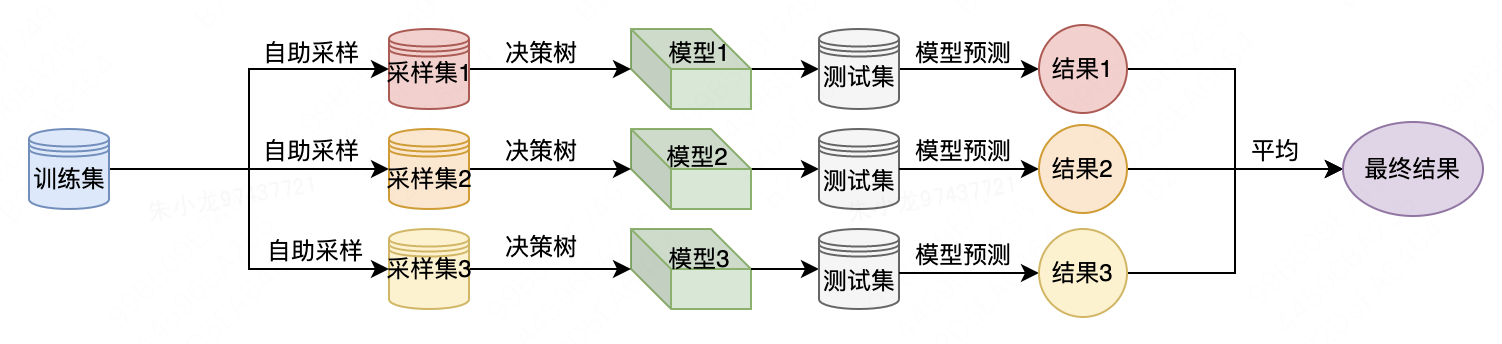
随机森林性能

我们先通过可视化看一下随机森林和每一颗决策树的结果。以下为使用sklearn包的实现代码。

import mglearn.plots
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

from data import two_moons


if __name__ == '__main__':
    X, y = two_moons.two_moons()
    # 数据集拆分
    X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
    # 创建一个随机森林分类器，包含 5 棵树，随机种子为 2
    forest = RandomForestClassifier(n_estimators=5, random_state=2)
    # 使用训练数据拟合模型
    forest.fit(X_train, y_train)

    # 创建一个 2x3 的图像，用于显示每棵树的分割情况
    fig, axes = plt.subplots(2, 3, figsize=(20, 10))
    # 遍历每棵树，显示其分割情况
    for i, (ax, tree) in enumerate(zip(axes.ravel(), forest.estimators_)):
        ax.set_title('Tree {}, score {:.2f}'.format(i, forest.estimators_[i].score(X_train, y_train)))
        # 绘制决策树
        mglearn.plots.plot_tree_partition(X_train, y_train, tree, ax=ax)

    # 在最后一个子图中显示整个随机森林的决策边界
    mglearn.plots.plot_2d_separator(forest, X_train, fill=True, ax=axes[-1, -1], alpha=0.4)
    axes[-1, -1].set_title('Random Forest, , score {:.2f}'.format(forest.score(X_train, y_train)))
    # 在前两个子图中显示训练数据的散点图
    mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)

运行代码后，可以得到下图。随机森林模型的结果，肉眼可见地优于一颗颗独立的决策树。从得分上来看，5颗决策树的值分别为0.88、0.93、0.93、0.95和0.84，而随机森林却将得分进一步提升到了0.96。

计算特征重要性就简单多了，一行代码就行：

forest.feature_importances_

以下为输出结果

array([0.38822127, 0.61177873])

在使用单决策树求解时，我们当时提到，重要性值分别为0.1478和0.2138。

看起来差异好像挺大，但其实是因为当时没有对重要性值做归一化处理。归一化后，第一个特征的重要性值为：
$$0.1478/(0.1478+0.2138)=0.4087$$
第二个特征的重要性值为：
$$0.2138/(0.1478+0.2138)=0.5913$$
现在看起来，两种方法下的差异就没那么大了。

随机森林特点

从本质上看，随机森林拥有决策树的所有优点。此外，在模型训练过程中，每一颗决策树的训练都可以并行执行，从而提升训练效率。

需要调节的重要参数有n_estimators和max_features。n_estimators指的是决策树数量，其总是越大越好。对更多的树取平均可以降低过拟合，从而得到鲁棒性更好的预测模型。不过收益是递减的，而且树越多需要的内存也越多，训练时间也越长。常用的经验法则就是“在你的时间/内存允许的情况下尽量多”。

max_features指的是每颗决策树所使用的特征数量。较小的max_features可以降低过拟合。一般来说，好的经验就是使用默认值：对于分类，默认值是max_features=sqrt(n_features)；对于回归，默认值是max_features=n_features。