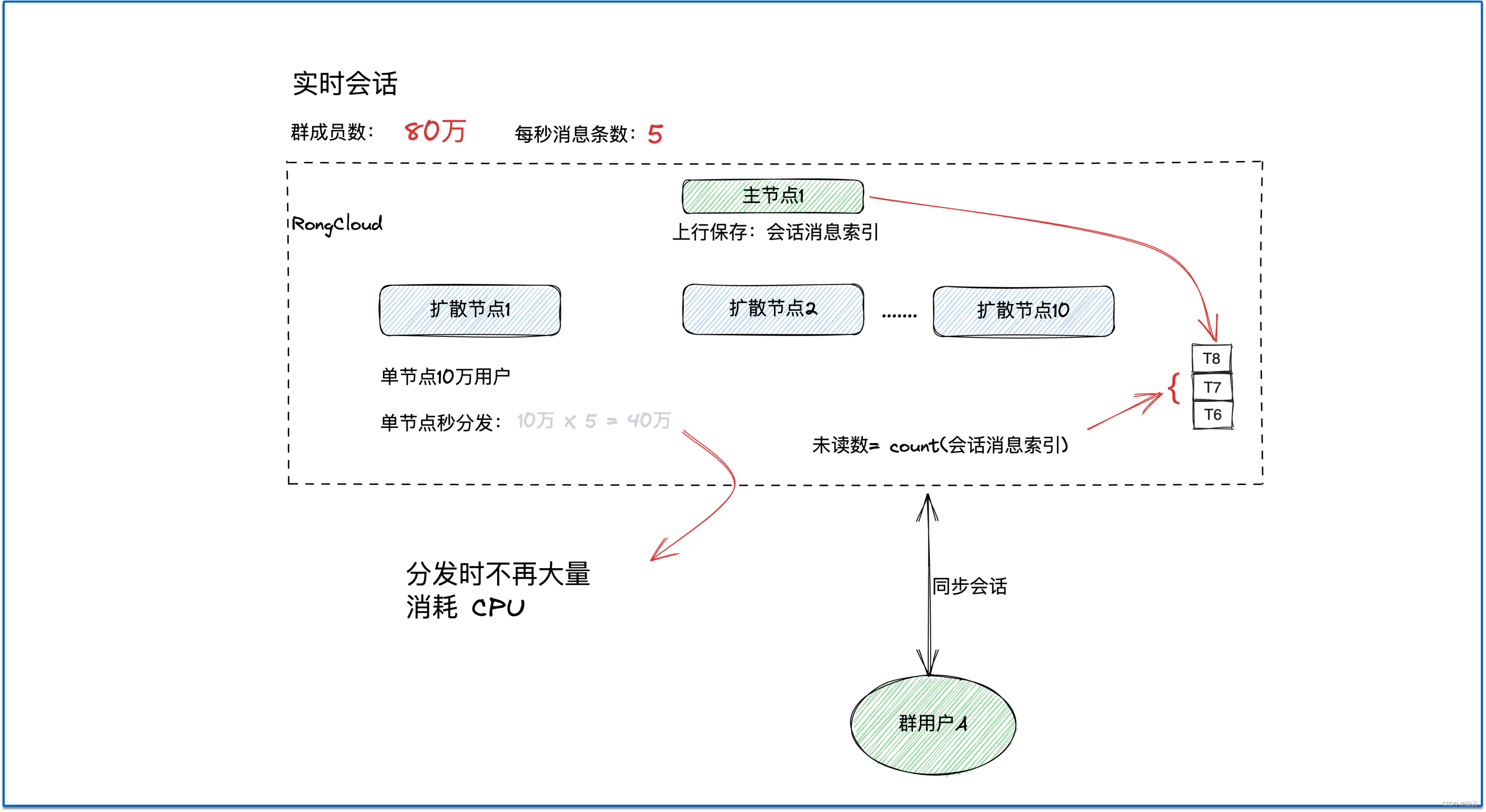
SiLu激活函数

在yolo v5中，我们使用了SiLu激活函数

首先，了解一下激活函数的作用：

激活函数在神经网络中起到了非常重要的作用。以下是激活函数的一些主要功能：

引入非线性：激活函数的主要目标是在模型中引入非线性。这是因为，如果没有激活函数，无论神经网络有多少层，它都只能表示线性函数。通过引入非线性，我们可以让神经网络更好地适应复杂的数据，模拟更复杂的函数。

决定神经元是否应被激活：激活函数定义了给定输入（包括偏置）时神经元输出的形式。换句话说，激活函数决定了神经元是否应该被激活。这是根据输入信息是否重要、是否需要被进一步传播来决定的。

帮助优化：激活函数和它们的导数（梯度）在反向传播过程中起到关键作用。在反向传播过程中，梯度被用来更新网络的权重和偏置。选择正确的激活函数可以帮助网络更快地收敛，并减少在训练过程中出现的问题，例如梯度消失或爆炸。

不同的激活函数有不同的特性，例如 Sigmoid，ReLU，tanh，Leaky ReLU，Swish 等，都有各自的优缺点。在实际使用中，选择哪种激活函数取决于具体的应用场景。

SiLu激活函数

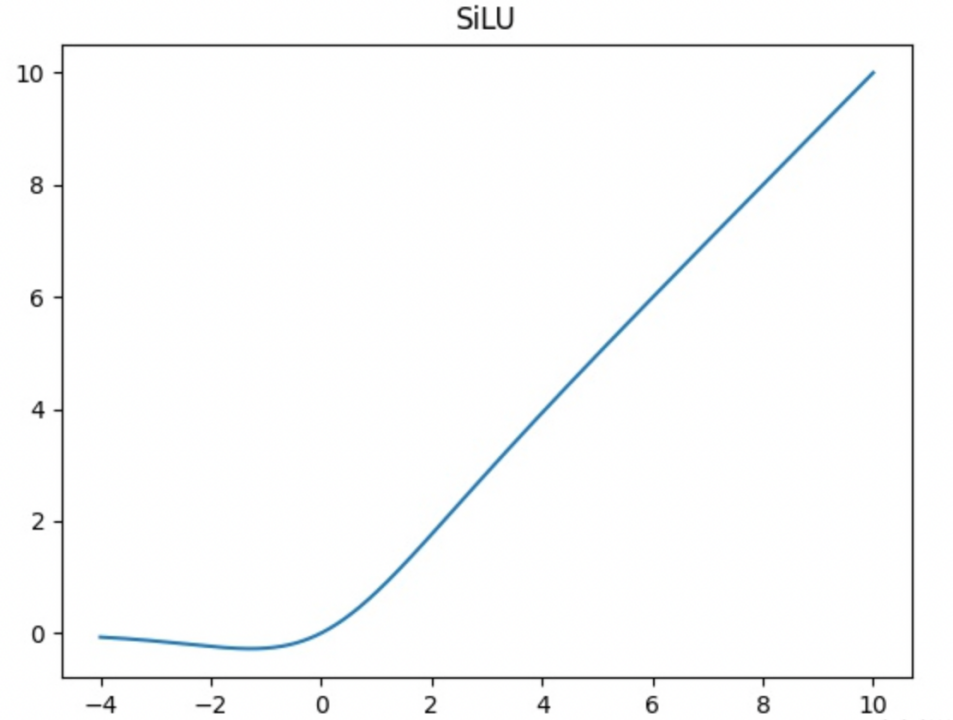
SiLU是Sigmoid和ReLU的改进版。SiLU具备无上界有下界、平滑、非单调的特性。SiLU在深层模型上的效果优于 ReLU。可以看做是平滑的ReLU激活函数。

SiLU（Sigmoid Linear Unit）激活函数也被称为 Swish 激活函数，它是 Google Brain 在 2017 年引入的一种自适应激活函数。

Swish 函数的定义如下：
f(x) = x * sigmoid(x)
其中 sigmoid(x) 是标准的 sigmoid 函数，它的值在 0 和 1 之间。Swish 函数的特性包括非线性，连续可导，并且在负无穷到正无穷的范围内都有定义。

Swish 函数在实践中已经证明了其有效性，特别是在深度神经网络中。它既有 ReLU（Rectified Linear Unit）激活函数的一些优点（例如，能够缓解梯度消失问题），又能解决 ReLU 函数的一些缺点（例如，ReLU 函数不是零中心的，且在负数部分的梯度为零）。此外，Swish 函数还是平滑函数，这意味着它在整个定义域内都有导数，这有利于优化。

代码：

class SiLU(nn.Module):
    @staticmethod
    def forward(x):
        return x * torch.sigmoid(x)