前言

文献阅读：一种预测中国东海岸非平稳和不规则波的VMD-LSTM/GRU混合模型

背景

研究区域和数据

VMD

LSTM/GRU预测模型

VMD-LSTM/GRU 方法的数值算法

序列的非平稳分析

神经网络设计

结论

代码：lstm预测污染物浓度

总结

前言

I read an article this week. This paper combines the advantages of LSTM model, GRU model and VMD technology to propose a VMD-LSTM/GRU model. (where LSTM is a variant of RNN and GRU is a variant of LSTM, VMD technology can effectively separate nonlinearity and non-smoothness in data.) This model is a good predictor of wave height at the seashore. It can also be applied to wave height prediction problems in other regions, and even to nonlinear prediction work in some areas.In addition to this, this week I am practicing practical applications of LSTM.

本周我读了一篇文章。本文结合LSTM模型、GRU模型和VMD技术的优点，提出了一种VMD-LSTM/GRU模型。（其中LSTM是RNN的变型，GRU是LSTM的变型，VMD技术可以有效地分离数据中的非线性和非平滑性。）这个模型可以很好的预测海边的海浪高度。它也可以应用于其他地区的波高预测问题，甚至可以应用于某些领域的非线性预测工作。除此之外，本周我在练习lstm的实际应用。

文献阅读：一种预测中国东海岸非平稳和不规则波的VMD-LSTM/GRU混合模型

--Lingxiao Zhao, Zhiyang Li, Leilei Qu, Junsheng Zhang, Bin Teng,
A hybrid VMD-LSTM/GRU model to predict non-stationary and irregular waves on the east coast of China,
Ocean Engineering,
Volume 276,
2023,
114136,
ISSN 0029-8018,
https://doi.org/10.1016/j.oceaneng.2023.114136.

背景

准确的波浪预报对于港口和海上结构操作以及船舶航行的安全至关重要。计算流体动力学（CFD）和传统的时间序列模型在处理非线性和非平滑性方面无效。然而，长短期记忆（LSTM）和栅极循环单元（GRU）具有很强的非线性处理能力，但在非平稳情况下存在缺陷。为避免现有波高预测方法的缺点，采用VMD方法对十分之一最高序列进行了预处理。变分模态分解（VMD）可以有效地分离数据中的非线性和非平滑性。基于长短期记忆（LSTM）和门循环单元（GRU）模型，使用GRU的更新和复位门代替LSTM的输入、遗忘和输出门。将混合LSTM/GRU模型与VMD算法相结合，构建VMD-LSTM/GRU模型，预测中国东部沿海2个站点非平稳波的十分之一最高。

研究区域和数据

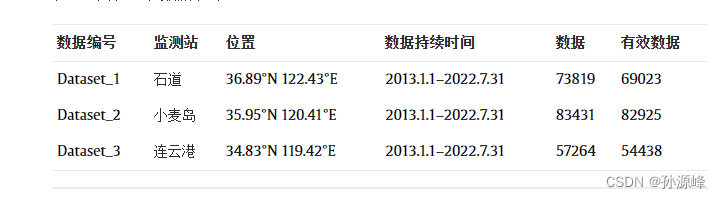
为了研究不同统计特征的预报模型的波浪效应，我们利用国家海洋数据中心、国家科技资源共享服务平台（http://mds.nmdis.org.cn/）从中国东部沿海的三个不同站点获取了十分之一的最高数据。选择这三个地点是为了确保它们包含不同的波高数据特征。

VMD

信号的电流处理通常使用经验模态分解（EMD）和变分模态分解（VMD）进行。EMD有几个缺点，例如存在模式混合，终点效应以及难以确定停止条件。为了克服这些限制，已经提出了VMD。变分模态分解（VMD）是一种用于模态变分分解和信号处理的自适应、完全非递归的方法（Sun 等人，2022 年）。该方法通常将一维输入信号分解为指定数量的K个内在模函数（IMF）。

与EMD的递归分解模式相比，VMD将信号分解转换为变分分解模式，本质上是一个多重自适应维纳滤波器组。VMD可以实现信号频域内各分量的自适应分割，可有效解决EMD分解过程中出现的模式重叠现象，噪声鲁棒性更强，终点效应比EMD弱。

$\alpha$ 是表示白噪声的方差正则化参数。

LSTM/GRU预测模型

GRU和LSTM可以选择性地记住重要信息并忘记不重要的信息。LSTM使用自己的三个门控设备来控制网络中的数据和信息流，从而解决了长期依赖的问题。然而，由于LSTM网络设置的参数过多，每个小区中有4个完全连接的层。在实际应用中，如果时间跨度大，LSTM网络深度深，则容易发生过拟合，计算处理要求高。与 LSTM 相比，GRU 用更新的门替换了 LSTM 的输入门、遗忘门和输出门Zt和复位门Rt.GRU 是 LSTM 的简化，参数更少，降低了过度拟合的风险。但是，在大型数据集的情况下，它的性能不如 LSTM。基于 LSTM 和 GRU 的复合 LSTM/GRU 模型保留了两种模型的优点，减少了过度拟合，并实现了高度准确的预测（ArunKumar 等人，2021 年）。

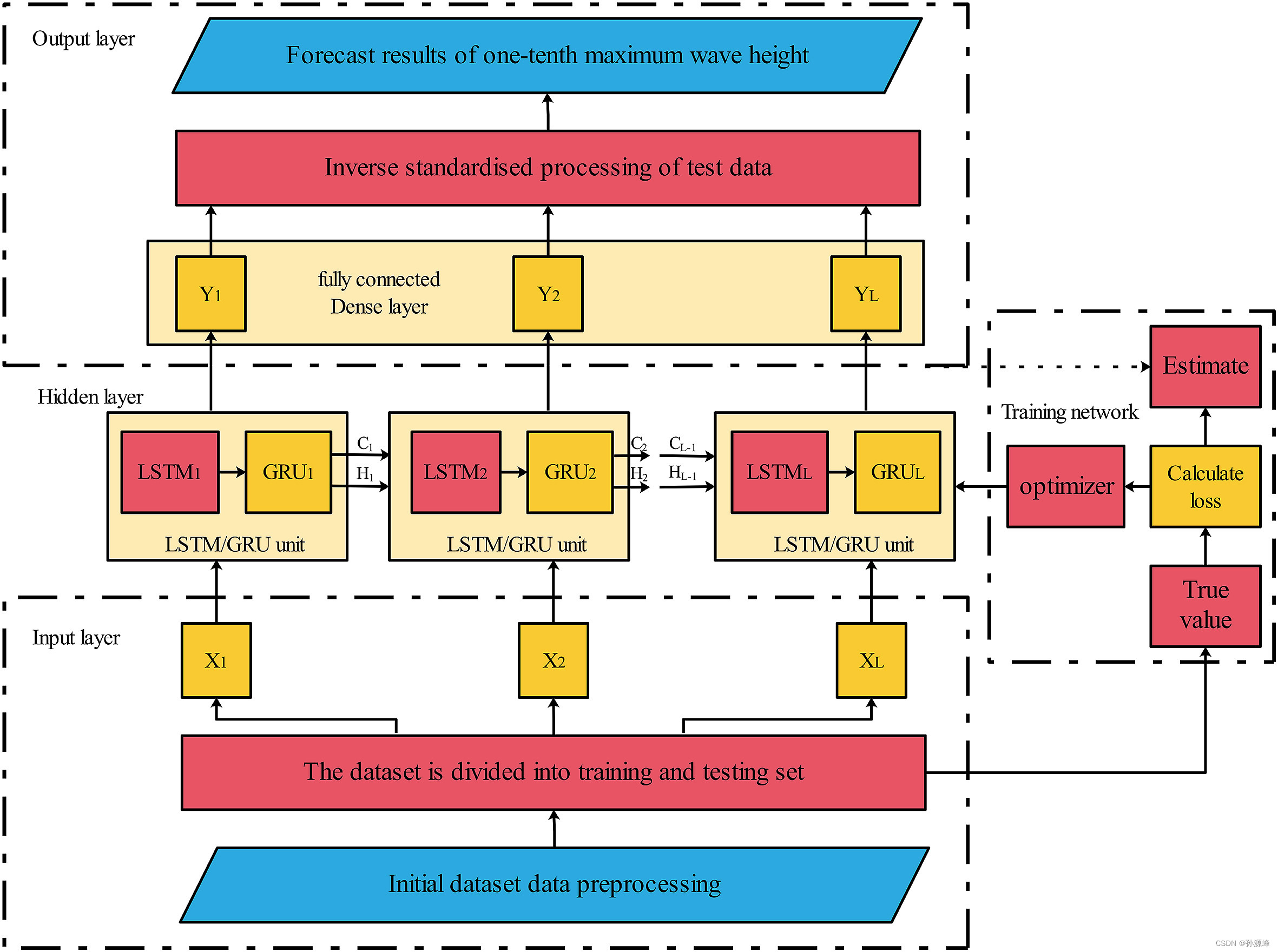
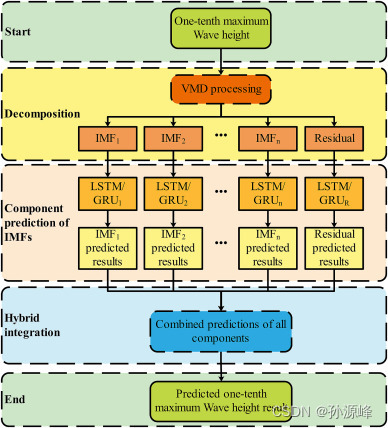
我们使用了混合LSTM/GRU门控长期和短期记忆网络，这是一种改进的RNN循环记忆网络算法，用于解决RNN在时间轴上对向后早期数据的“体重遗忘”或“梯度消失”问题。具体预测模型的整体框架如下图 2 所示，包含以下 4 个组件

VMD-LSTM/GRU 方法的数值算法

在自然海洋中，波浪是具有非平稳性特征和复杂的不规则非线性变化的时间序列。一般来说，不规则波浪在海洋和近海工程中是一个难以分析的问题。尽管可以使用计算流体动力学（CFD）以数值方式解决这个问题，但这种方法受到长计算周期和大量资本支出的抑制（Vardaroglu 等人，2022 年）。

VMD和LSTM/GRU模型的结合是预测非平稳性和不规则非线性波的有效方法。使用VMD-LSTM/GRU方法进行波浪预报的过程包括三个步骤，如图3所示。第一步是将去掉缺失值的波高时间序列数据分解为基于VMD算法的几组简单平滑的本征模态函数（IMF）和残差。第二步是使用LSTM/GRU模型分别预测基金组织的每个组成部分。最后，对各分量的预测进行聚合，得到最终的预测结果。

序列的非平稳分析

对于十分之一最高的非平滑特性，Duan等人（2016b）使用递归图分析了波高数据中的非平稳行为，并使用经验模态分解（EMD）算法处理非平滑时间序列。他们得出的结论是，如果时间序列是平滑的，则递归图应均匀分布。相反，如果时间序列是非平稳的，则递归图是非均匀分布的。根据研究结果，可以观察到所分析的Pogo时间序列的递归图是非均匀分布的，表明Pogo具有非平稳性的特征。

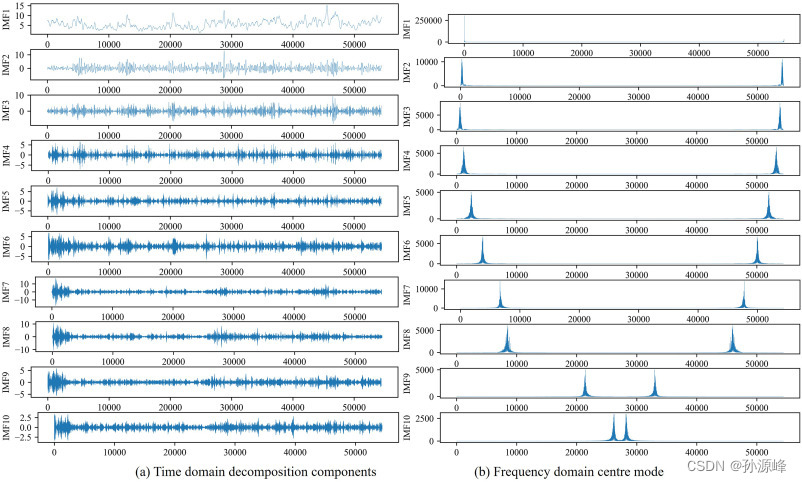
EMD算法处理非平稳时间序列的有效性也在Hao等人（2022）的研究中得到了证实。鉴于VMD算法与非平稳时间序列的EMD算法相比具有更好的性能（Abdoos，2016），本报告使用这种方法来分析非平稳特性，以可能获得更准确的预测结果。基于VMD算法，将十分之一的最高数据集分解为几个IMF分量和残差，如图6、图8和10所示。很明显，使用VMD算法将dataset_1-dataset_3的复杂波时间序列分解为几个简单的时程分量。

神经网络设计

神经网络的预测准确性可以通过添加更多层或更多神经元来提高。然而，在某些情况下添加更多的层和神经元不利于提高神经网络的准确性，同时增加训练时间。在这项研究中，LSTM/GRU网络结构模型中的隐藏神经元层数设置为3，隐藏层中的每一层包含200个神经元。最后，有一个只有一个神经元的全连接层，该层的输出大小等于预测结果的大小。回归层计算半均方误差损失以监控网络的收敛性。

该模型是使用带有深度学习工具箱的 MATLAB R2022a 实现的。在此网络中，不需要 dropout 图层，因为数据集的大小足够大以防止过度拟合。基于自适应矩估计（Adam）优化器进行训练。对于调查中使用的三个数据集，最大 Epochs 的迭代次数为 500，迷你批大小为 16。初始学习率、学习率下降因子和学习率下降周期分别为0.005、0.2和100，采用分段学习率时间表。

结论

非平稳特性对波浪预报的性能有重要影响。时间序列中的非平稳特征会导致 LSTM 模型和 GRU 模型的预测出现明显的相位偏差，从而导致预测性能不佳。此外，非平滑特征对模型预测性能的影响与预测持续时间成正比。当预测持续时间较短时，非平滑度的影响会降低。随着预测持续时间的增加，其效果逐渐增加，相移引起的误差也逐渐增加。

本报告从国家海洋数据中心、国家科技资源共享服务平台获得中国东部沿海不同地理位置十分之一的最高。然后使用LSTM/GRU模型构建VMD-LSTM/GRU模型进行波浪预报。其次，通过对比LSTM、GRU、LSTM/GRU和VMD-LSTM/GRU模型，确定VMD算法在平滑波浪时间序列后能有效提高波浪预测结果的精度;随着预测持续时间的增加，非平滑性的影响逐渐增大，LSTM、GRU和LSTM/GRU模型的预测相移逐渐增大。特别是，对于2 h预测持续时间，LSTM / GRU模型具有很高的精度。然而，在10 h预报时间内，LSTM/GRU模型的准确性不再满足准确预测的要求。最后，通过研究两种模型的误差模式，确定采用VMD算法对波浪时间序列进行平滑处理后，VMD-LSTM/GRU模型的预测精度显著提高，有效抑制了非平滑性对预测性能的影响。主要调查结果如下。

(1)当使用VMD-LSTM/GRU模型进行波浪预报时，结果揭示了波浪的总体趋势，并捕捉了局部峰谷的波动，从而大大提高了预测精度。

(2)波浪时间序列的非平稳性恶化了模型的预测性能。LSTM模型和GRU模型在非平稳时间序列数据方面存在一定的局限性，导致预测结果与实际结果之间存在相位偏差。

(3)利用VMD算法对波浪时间序列进行预处理，提高了LSTM/GRU模型预测结果与实际结果的相关性。与单独的LSTM和GRU模型相比，拟议的VMD-LSTM / GRU模型表现出更高的性能。当预测时间增加时，非平滑性变得明显。这表明VMD算法能够有效解决时间序列的非平稳性问题，提高十分之一最高的预测性能。

该模型对来自国家海洋数据中心、国家科技资源共享服务平台的三个位置的不同数据集表现出良好的预测。鉴于三个数据集不同，差异是显着的。因此，混合VMD-LSTM/GRU模型对这三个数据集的良好预测表明该模型具有良好的迁移和泛化属性。它可以应用于其他地区的波高预测问题，甚至可以应用于某些领域的非线性预测工作。

尽管该模型具有上述优点，但我们没有考虑有关三个调查区域的地理位置的信息。这意味着混合 VMD-LSTM/GRU 方法仅对时态信息进行建模，而不对空间信息进行建模。此外，不同地区的波浪并非相互独立;它们之间有一些耦合。应开展进一步研究，提取和分析空间信息。未来，高级特征提取算法可能会与机器学习相结合，以进一步提高性能。

代码：lstm预测污染物浓度

date,pollution
2010-01-01,0.5
2010-01-02,0.6
2010-01-03,0.4
...
import pandas as pd
import numpy as np

# 加载数据
data = pd.read_csv('data.csv')

# 将日期列转换成时间戳索引
data['date'] = pd.to_datetime(data['date'])
data.set_index('date', inplace=True)

# 归一化处理
data = (data - data.min()) / (data.max() - data.min())

# 构建监督学习数据集
lag = 30  # 时间步长
X = []
y = []
for i in range(len(data) - lag):
    X.append(data[i:i+lag].values)
    y.append(data.iloc[i+lag])
X = np.array(X)
y = np.array(y)

# 划分训练集和测试集
split = int(len(X) * 0.8)
X_train, X_test = X[:split], X[split:]
y_train, y_test = y[:split], y[split:]
from keras.models import Sequential
from keras.layers import LSTM, Dense

# 构建模型
model = Sequential()
model.add(LSTM(64, input_shape=(lag, 1)))
model.add(Dense(1))
model.compile(loss='mse', optimizer='adam')

# 训练模型
model.fit(X_train, y_train, epochs=100, batch_size=32)
from sklearn.metrics import mean_squared_error

# 预测测试集
y_pred = model.predict(X_test)

# 反归一化处理
y_test = y_test * (data.max() - data.min()) + data.min()
y_pred = y_pred * (data.max() - data.min()) + data.min()

# 评估模型
mse = mean_squared_error(y_test, y_pred)
print('MSE:', mse)

如果要增加影响因素，可以考虑将其他相关的变量加入到模型中，例如天气、风向、风速等。这样可以提高模型的预测准确度。

下面是一个增加天气和风向作为影响因素的代码示例：

在这个示例中，我们将天气和风向信息加入到了数据集中，并对离散变量进行了独热编码。然后，我们重新构建了监督学习数据集，并修改了LSTM模型的输入维度。最后，我们在测试集上进行预测，并进行了反归一化处理和评估模型的表现。

import pandas as pd
import numpy as np

# 加载数据
data = pd.read_csv('data.csv')

# 将日期列转换成时间戳索引
data['date'] = pd.to_datetime(data['date'])
data.set_index('date', inplace=True)

# 增加天气和风向列，假设我们有一份天气数据和风向数据
weather = pd.read_csv('weather.csv')
wind = pd.read_csv('wind.csv')

data['weather'] = weather['weather']
data['wind_direction'] = wind['direction']

# 将离散变量进行编码
data = pd.get_dummies(data, columns=['weather'])

# 归一化处理
data = (data - data.min()) / (data.max() - data.min())

# 构建监督学习数据集
lag = 30  # 时间步长
X = []
y = []
for i in range(len(data) - lag):
    X.append(data[i:i+lag].values)
    y.append(data.iloc[i+lag])
X = np.array(X)
y = np.array(y)

# 划分训练集和测试集
split = int(len(X) * 0.8)
X_train, X_test = X[:split], X[split:]
y_train, y_test = y[:split], y[split:]

# 构建模型
from keras.models import Sequential
from keras.layers import LSTM, Dense

model = Sequential()
model.add(LSTM(64, input_shape=(lag, X_train.shape[2])))
model.add(Dense(1))
model.compile(loss='mse', optimizer='adam')

# 训练模型
model.fit(X_train, y_train, epochs=100, batch_size=32)

# 预测测试集
y_pred = model.predict(X_test)

# 反归一化处理
y_test = y_test * (data.max() - data.min()) + data.min()
y_pred = y_pred * (data.max() - data.min()) + data.min()

# 评估模型
from sklearn.metrics import mean_squared_error

mse = mean_squared_error(y_test, y_pred)
print('MSE:', mse)