💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
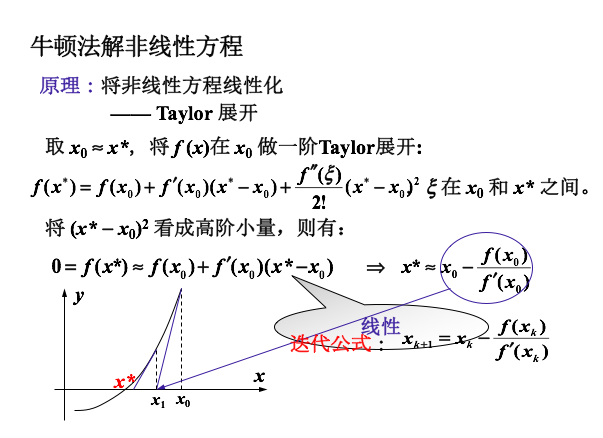
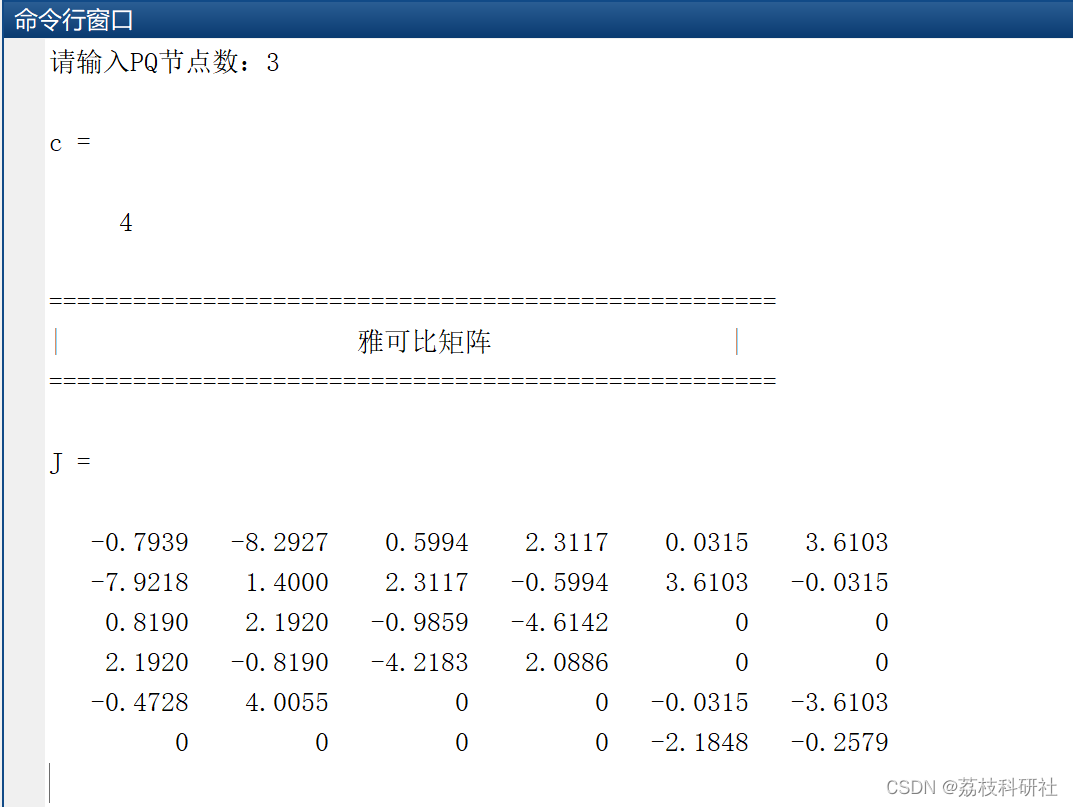
2.1 雅可比矩阵
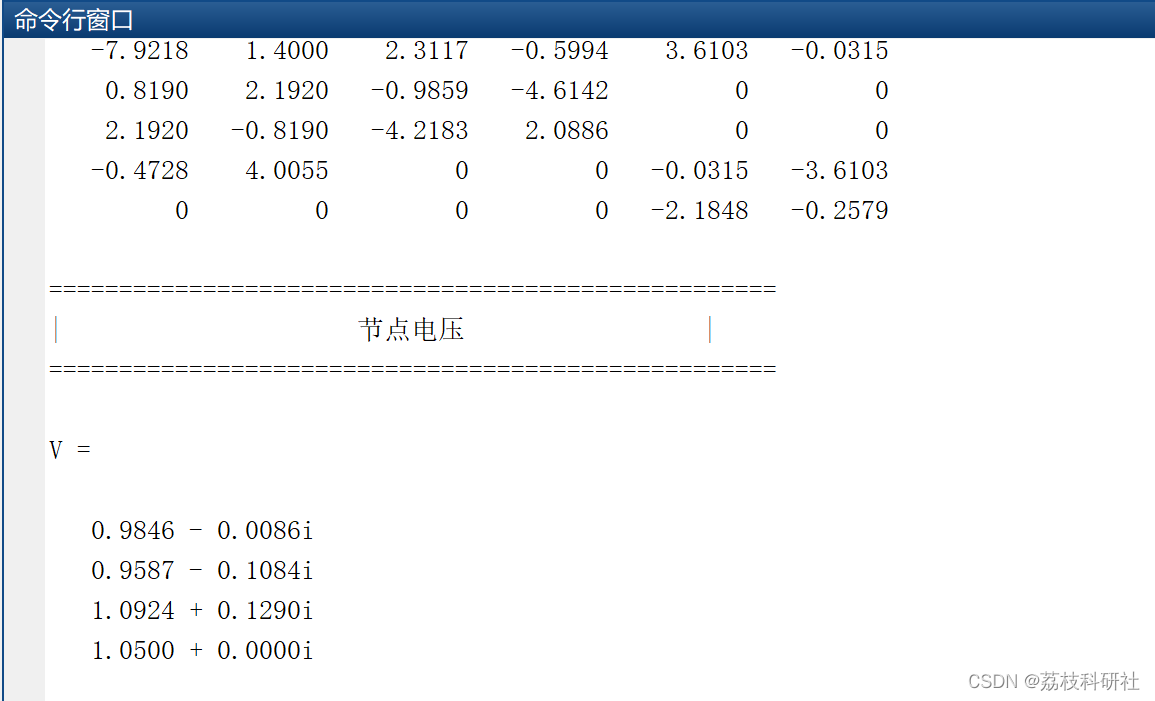
2.2 节点电压
2.3 节点负荷
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
牛顿-拉夫逊法在数学上是求解非线性代数方程式的有效方法。
其要点是把非线性方程式的求解过程变成反复地对相应的线性方程式进行求解的过程,即通常所称的逐次线性化过程。是数值计算普遍使用的重要方法,以开方运算为例,求平方根不是四则运算,因此在计算机上求平方根使用牛顿-拉夫逊迭代法来转化为四则运算进行求解。
牛顿 迭代法 ( Newton's method )又称为 牛顿-拉夫逊(拉弗森)方法(Newton-Raphson method) ,它是 牛顿 在17世纪提出的一种在 实数 域和 复数 域上近似求解方程的方法。多数方程不存在求根公式,因此求精确根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要。方法使用函数f(x)的 泰勒级数 的前面几项来寻找方程f(x) = 0的根。牛顿迭代法是求方程根的重要方法之一,其最大优点是在方程f(x) = 0的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根,此时线性收敛,但是可通过一些方法变成超线性收敛。另外该方法广泛用于计算机编程中。
📚2 运行结果
2.1 雅可比矩阵
2.2 节点电压
2.3 节点负荷

请输入PQ节点数:3
c =
4
====================================================
| 雅可比矩阵 |
====================================================J =
-0.7939 -8.2927 0.5994 2.3117 0.0315 3.6103
-7.9218 1.4000 2.3117 -0.5994 3.6103 -0.0315
0.8190 2.1920 -0.9859 -4.6142 0 0
2.1920 -0.8190 -4.2183 2.0886 0 0
-0.4728 4.0055 0 0 -0.0315 -3.6103
0 0 0 0 -2.1848 -0.2579====================================================
| 节点电压 |
====================================================V =
0.9846 - 0.0086i
0.9587 - 0.1084i
1.0924 + 0.1290i
1.0500 + 0.0000i====================================================
| 节点负荷 |
====================================================S =
-0.3000 -0.1800
-0.5500 -0.1300
0.5000 0.0934
0.3679 0.2647>>
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]蒋焱. 配电网潮流计算理论算法研究与程序实现[D].南昌大学,2020.DOI:10.27232/d.cnki.gnchu.2020.001258.
[2]叶帆. 配电网潮流计算的分析与运用[D].南昌大学,2015.