【人工智能】— 监督学习、分类问题、决策树、线性分类器、K近邻、回归问题、交叉验证
- 监督学习 - 正式设置
- 符号表示
- 假设选择
- 学习目标
- 预测
- 分类
- Decision Trees 决策树
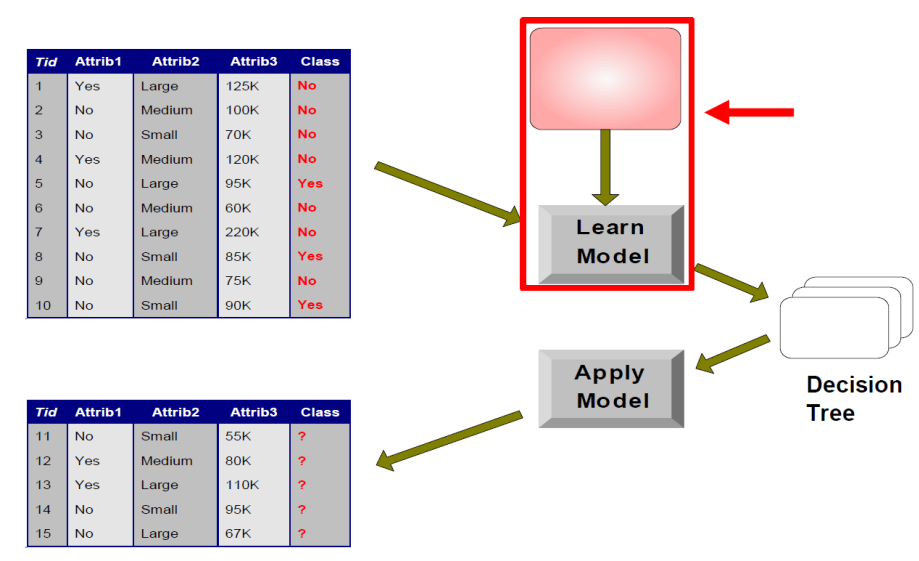
- 建立决策树分类模型的流程
- 如何建立决策树?
- 决策树学习
- 表达能力
- 决策树学习
- 信息论在决策树学习中的应用
- 特征选择准则一:信息增益
- 举例
- 结论
- 不足
- 回到餐厅的例子
- 从12个例子中学到的决策树:
监督学习 - 正式设置
监督学习是一种学习框架,其中给定一组输入和输出示例 ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) (x_1, y_1), (x_2, y_2), ..., (x_N, y_N) (x1,y1),(x2,y2),...,(xN,yN),目标是学习一个函数 f ( x ) f(x) f(x),该函数可以将新的输入映射到相应的输出。
符号表示
- 输入空间: X X X
- 输出空间: Y Y Y
- 输入: x ∈ X x \in X x∈X
- 输出: y ∈ Y y \in Y y∈Y
- 训练数据集: D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } D = \{(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)\} D={(x1,y1),(x2,y2),...,(xN,yN)}
- 假设集合: H = { f ∣ f : X → Y } H = \{f | f:X \rightarrow Y\} H={f∣f:X→Y}
假设选择
监督学习的目标是学习一个函数 f ( x ) f(x) f(x),它可以将输入映射到输出。这个函数通常被选择为假设集合 H H H 中的一个函数。假设集合 H H H 可以选择为一组函数类,例如线性模型、决策树、神经网络等。在选择假设集合时,通常考虑模型的表达能力和复杂度。
学习目标
监督学习的目标是学习一个函数 f ( x ) f(x) f(x),使得该函数可以将输入映射到相应的输出。具体来说,学习目标是找到一个函数 f ∈ H f \in H f∈H,使得对于所有的 ( x i , y i ) ∈ D (x_i, y_i) \in D (xi,yi)∈D, f ( x i ) f(x_i) f(xi) 的输出与 y i y_i yi 相匹配。这个过程通常使用训练数据集 D D D 来进行,其中学习算法通过最小化模型与真实值之间的误差来寻找最佳假设 f f f。
预测
一旦找到了最佳假设 f f f,我们可以将新的输入 x N + 1 x_{N+1} xN+1 映射到相应的输出 y N + 1 y_{N+1} yN+1,即 y N + 1 = f ( x N + 1 ) y_{N+1} = f(x_{N+1}) yN+1=f(xN+1)。
分类
分类是一种监督学习任务,旨在根据观测到的特征将数据点分配到已知类别中的一个。具体来说,我们被给定 N N N 个观测值 { ( x i , y i ) } i = 1 N \{(x_i, y_i)\}_{i=1}^N {(xi,yi)}i=1N,其中 x i ∈ X x_i \in X xi∈X 是一个特征向量, y i ∈ Y y_i \in Y yi∈Y 是标签或类别。任务是将新的输入 x ∈ X x \in X x∈X 映射到相应的标签 y ∈ Y y \in Y y∈Y。
例如,在图像分类任务中,输入 x x x 可能是一幅图像,而标签 y y y 可能是描述图像内容的类别,如“狗”、“猫”、“汽车”等。
分类任务通常被分为两类:二分类和多分类。在二分类任务中,标签 y y y 只有两个可能的值。在多分类任务中,标签 y y y 可以有多个可能的值。
分类问题的解决方法通常是学习一个分类器,该分类器使用训练数据集中的特征和标签来预测新的未标记数据点的标签。常见的分类器包括逻辑回归、支持向量机、决策树、随机森林、朴素贝叶斯等。
Decision Trees 决策树
什么是决策树 —— 基本概念
- 非叶节点:一个属性上的测试,每个分枝代表该测试的输出
- 叶节点:存放一个类标记
- 规则:从根节点到叶节点的一条属性取值路径
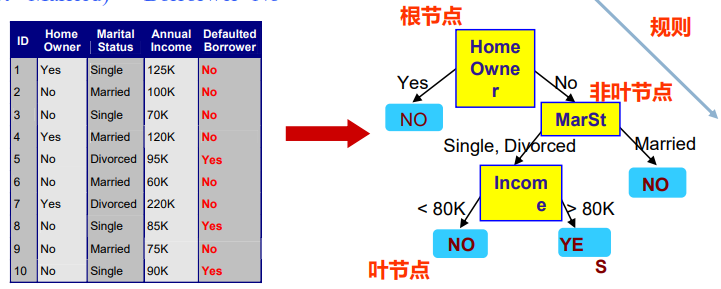
建立决策树分类模型的流程
- 模型训练:从已有数据中生成一棵决策树
- 分裂数据的特征,寻找决策类别的路径
- 相同的数据,根据不同的特征顺序,可以建立多种决策树
如何建立决策树?
基本的决策树学习过程,可以归纳为以下三个步骤:
- 特征选择:选取对于训练数据有着较强区分能力的特征
- 生成决策树:基于选定的特征,逐步生成完整的决策树
- 决策树剪枝:简化部分枝干,避免过拟合因素影响
决策树学习
问题:基于以下属性,决定是否在餐厅等待桌子:
- Alternate:附近是否有其他选择的餐厅?
- Bar:是否有一个舒适的酒吧区等待?
- Fri/Sat:今天是星期五还是星期六?
- Hungry:我们饿了吗?
- Patrons:餐厅里的人数(无人、有些人、满座)
- Price:价格范围(
$、$$、$$$) - Raining:外面是否下雨?
- Reservation:我们是否预约了?
- Type:餐厅类型(法国、意大利、泰国、汉堡)
- WaitEstimate:等待时间的预估值(0-10、10-30、30-60、>60)
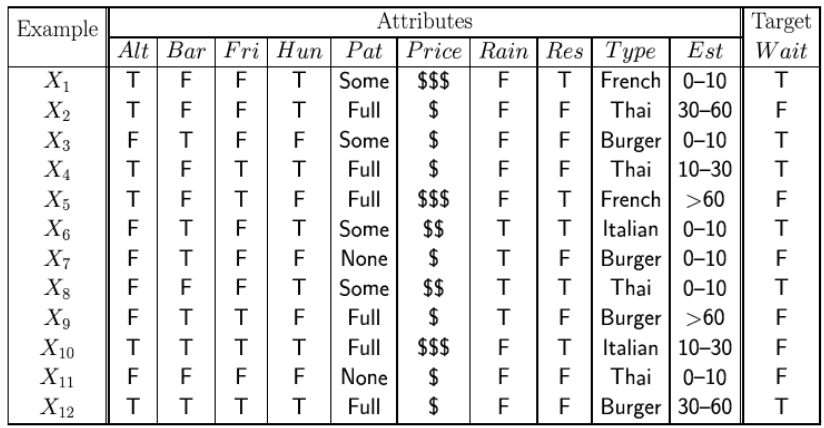
假设的一种可能表示
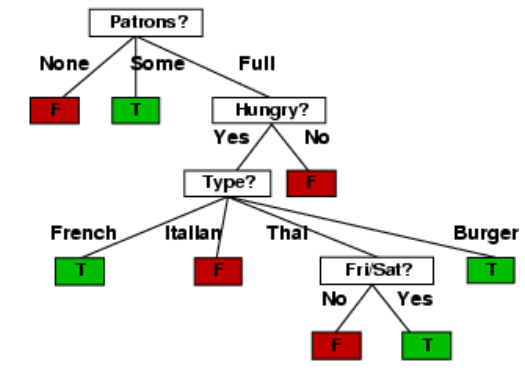
例如,在上述餐厅等待桌子的问题中,我们可以使用决策树来表示假设,该决策树定义了在不同属性值下等待桌子的决策。以下是一个可能的假设树示例: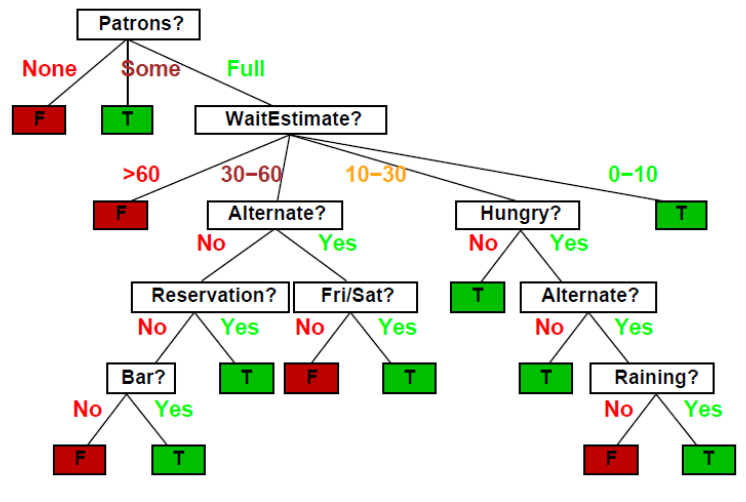
表达能力
决策树可以表示任何输入属性的函数,但使用单条路径来表示每个训练示例的决策树可能会过度拟合数据,无法很好地推广到新的未见过的数据示例。
决策树可以表达输入属性的任何函数。例如,对于布尔函数,函数真值表的每行对应于树中 的一条路径: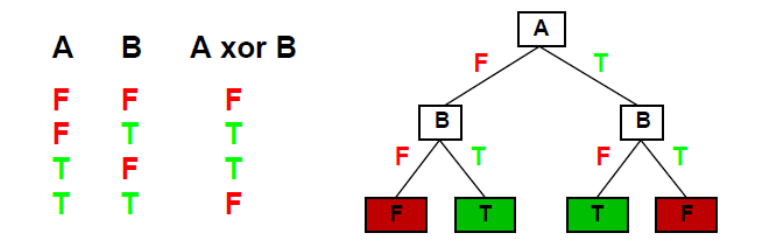
简单来说,针对每个训练示例,可以创建一条路径到叶子节点的一致性决策树(除非函数在输入属性上是非确定性的),但这种决策树可能会过度拟合数据,无法很好地泛化到新的未见过的数据示例。因此,更倾向于找到更紧凑的决策树来提高泛化性能。
决策树学习
目的:找到一个与训练示例一致的小树
想法:(递归)选择“最重要”属性作为(子)树的根

想法:一个好的属性将示例拆分为(理想情况下)“全正”或“全负”的子集
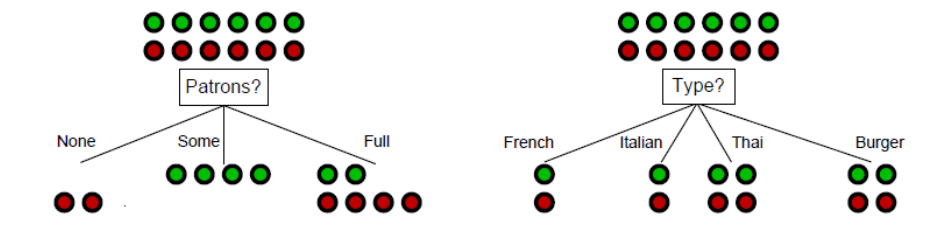
根据Patron分类是一个更好的选择
信息论在决策树学习中的应用
信息熵:计算数据的不确定性
Entropy
(
t
)
=
−
∑
j
=
1
m
p
(
j
∣
t
)
log
2
p
(
j
∣
t
)
\text{Entropy}(t) = - \sum_{j=1}^m p(j|t) \log_2 p(j|t)
Entropy(t)=−j=1∑mp(j∣t)log2p(j∣t)
此时:表示某个节点𝑡 (即某个特征)的信息不确定性
p
(
j
∣
t
)
p(j|t)
p(j∣t)是节点特征𝑡的属于类别𝑗的样本的比例
- 特点:对于该节点特征t
- 当样本均匀地分布在各个类别时,熵达到最大值 l o g ( n c ) log(n_c) log(nc), 此时包含的信息最少
- 当样本只属于一个类别时,熵达到最小值 0, 此时包含的信息最多
对于包含 p p p 个正例和 n n n 个反例的训练集,其熵可以用以下公式计算:
I ( p p + n , n p + n ) = − p p + n log 2 p p + n − n p + n log 2 n p + n I(\frac{p}{p+n},\frac{n}{p+n}) = -\frac{p}{p+n}\log_2\frac{p}{p+n}-\frac{n}{p+n}\log_2\frac{n}{p+n} I(p+np,p+nn)=−p+nplog2p+np−p+nnlog2p+nn
其中,第一项和第二项分别表示正例和反例的占比, log 2 \log_2 log2 表示以 2 为底的对数。熵的值越高,表示数据集越不确定。

特征选择准则一:信息增益
信息增益: 按某个特征划分之后,数据不确定性降低的程度
Gain ( m ) = Entropy ( p ) − ( ∑ i = 1 k ∣ n i ∣ n Entropy ( i ) ) \text{Gain}(m) = \text{Entropy}(p) - (\sum^k_{i=1} \frac{|n_i|}{n}\text{Entropy}(i)) Gain(m)=Entropy(p)−(i=1∑kn∣ni∣Entropy(i))
- 第一项 Entropy ( p ) \text{Entropy}(p) Entropy(p)表示数据未划分时的信息熵
- 第二项
∑
i
=
1
k
∣
n
i
∣
n
Entropy
(
i
)
\sum^k_{i=1} \frac{|n_i|}{n}\text{Entropy}(i)
∑i=1kn∣ni∣Entropy(i)表示按特征m划分后,数据的信息熵
- 按特征 m m m划分后,父节点分裂成 k k k个子节点
- 𝑛表示父节点的样本个数
- 𝑛𝑖 表示子节点𝑖的样本个数
选择准则:选择最大的𝐺𝐴𝐼N 对应的特征m
举例
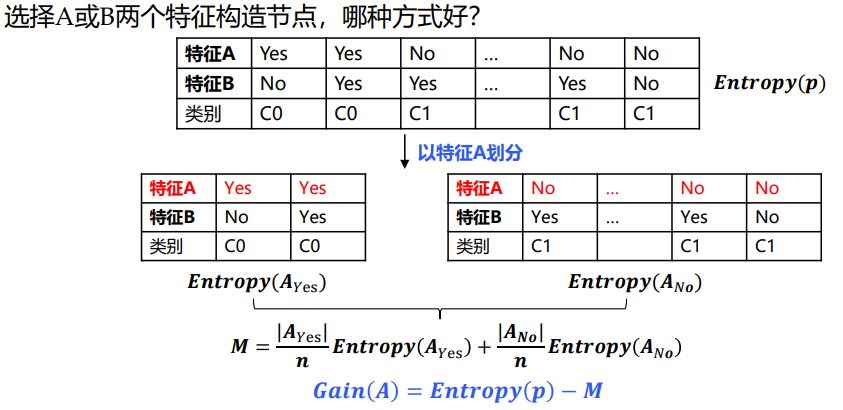
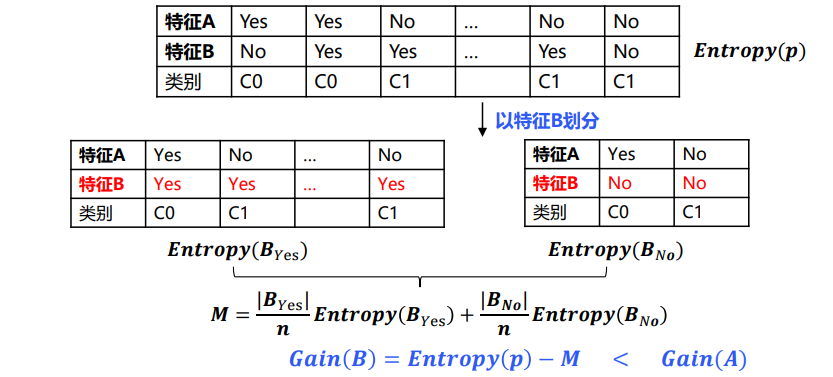
结论
信息增益能够较好地体现某个特征在降低信息不确定性方面的贡献
信息增益越大,说明信息纯度提升越快,最后结果的不确定性越低
不足
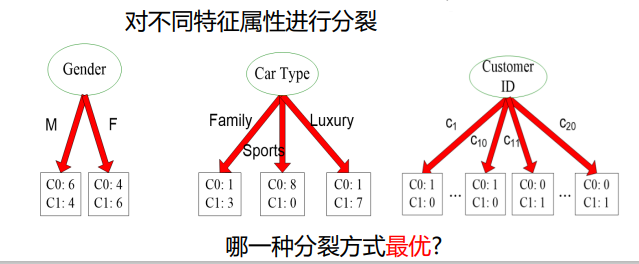
信息增益的局限性,尤其体现在更偏好可取值较多的特征
取值较多,不确定性相对更低,因此得到的熵偏低,但不一定有实际意义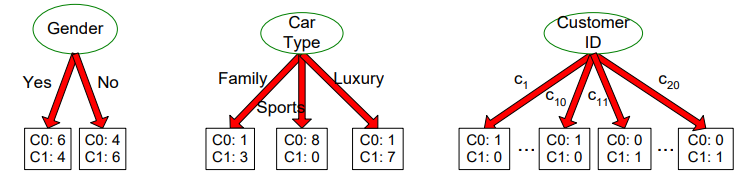
特征Customer ID有最大的信息增益,因为每个子节点的熵均为0
回到餐厅的例子
对于训练集,
p
=
n
=
6
p=n=6
p=n=6,信息熵为
I
(
6
12
,
6
12
)
=
1
I(\frac{6}{12}, \frac{6}{12})=1
I(126,126)=1 bit。
考虑属性Patrons和Type(以及其他属性)
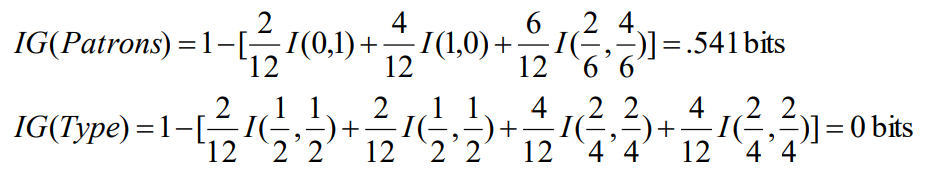
从12个例子中学到的决策树: