本文作为对图结构和复杂网络的快速上手，内容包括图基础知识，NetworkX使用，一个NetworkX构建实体关系和可视化的案例

图的基础知识

1.1 图（graph）及其分类

（1） 图的定义：图是由点集$V=v_i$以及V中元素无序对的集合$E=e_k$所构成的二元组，记为$G=(V,E)$，V中的元素$v_i$称为节点，E中的元素$e_k$称为边。通俗理解：图是节点和边构成及集合。
（2） 简单图：不含环和多重边的图称为简单图；多重图：含有多重边的图
（3） 完全图：每一对节点之间都有边相连的简单图称为完全图；有向完全图： 每一对节点间有且仅有一条有向边的简单图
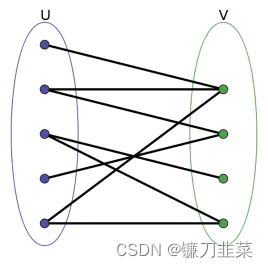
（4） 二部图：图$G(V,E)$的点集V可以分成两个非空子集X,Y，即X并Y等于V，X交Y等于空集，如果E中的每条边的两个端点必有一个属于X，另一端点属于Y，则成G为二部图，有时记为：$G=(X,Y,E)$

1.2 节点的度（degree）

（1） 节点的度的定义：与节点（node）V相连的边（edge）数之和称为节点的度，记为deg（v），简记为：d（v）
（2） 悬挂点：度为1的节点称为悬挂点；悬挂边：连接悬挂点的边称为悬挂边
（3） 任何图中，节点的度之和等于边数的2倍，次数为奇数的节点必为偶数个。
（4） 出度：在有向图中，以节点$v_i$为起始点的边数称为出度；入度：在有向图中，以节点$v_i$为终止点的边数称为入度

1.3 子图（subgraph）

（1）图G=(E,V)，若E’是E的子集，V’是V的子集，且E’中的边仅与V’中的节点相关联，则称$G’=(V’,E’)$是G的一个子图。

1.4 连通图

（1）各边相异的道路称为迹（trace），也成为简单路径（simple path）；各节点相异的道路称为（track），也称为基本路径（essential path）；起点和终点重合的道路称为回路（circuit），否则称为开路（open circuit）。
（2）连通图：图中任意两点间至少有一条道路相连，则称该图为连通图。

1.5 图的矩阵表示

赋权图$G=(E,V)$,其边$(v_i，v_j)$有权$w_{ij}$，构造矩阵$A=(a_{ij})$，则称矩阵A为赋权图G的邻接矩阵。

NetworkX概述

NetworkX是一个Python包，用于创建、操作和研究复杂网络的结构、动力学和功能。使用NetworkX，可以以标准和非标准数据格式加载和存储网络，生成多种类型的随机和经典网络，分析网络结构，构建网络模型，设计新的网络算法，绘制网络，等等

networkx包安装

$ pip install networkx

NetworkX基础教程

主要包括创建图，节点，边，访问图元素，添加图属性，清空图，图可视化，图持久化，从外部文件读取图数据等

1. 创建图

首先创建一个空图，这个空图没有任何节点和边，且这个空图是一个无向图nx.Graph:

import networkx as nx
G = nx.Graph()

根据定义，图是节点（顶点）以及已识别的节点对（称为边，链接等）的集合。在 NetworkX 中，节点可以是任何可哈希(hashable)对象，例如，文本字符串、图像、XML对象、另一个图、自定义节点对象等。

python 中的None不能作为节点。

2. 节点

图可以以多种形式扩张。NetworkX包括许多图生成函数和工具，用于读取和写入多种格式的图。
作为简单开始，可以使用add_node每次添加一个节点：

G.add_node(1)

或者从可迭代容器(iterable)（如列表）中添加多个节点：

G.add_nodes_from([2, 3])
G.add_nodes_from("spam")  # 字符串可迭代对象，实际增加的是4个节点: 's', 'p', 'a', 'm'

也可以在添加节点的时候增加节点的属性，但是有格式要求，在add_nodes_from中将每个节点元素设置为元组格式并且，元组内指定属性为字典结构(node, node_attribute_dict)：

G.add_nodes_from([
    (4, {"color": "red"}),
    (5, {"color": "green"}),
])

一个图中的节点可以合并到另一个图，同样是使用add_nodes_from：

H = nx.path_graph(10)  # path_graph是生成一个由n-1条边线性连接的n个节点的路径图
G.add_nodes_from(H)

现在图G中节点包括原H中的节点。相反，也可以将整个图H作为图G中的一个节点：

G.add_node(H)

现在图G 将图H作为其中一个节点。这种灵活性非常强大，因为它允许图形组成的图形，文件组成的图形，函数组成的图形等等。值得考虑如何构建应用程序，以便节点是有用的实体。当然，如果您愿意，您始终可以在G中使用唯一标识符，并按标识符键记节点信息的单独字典。

如果哈希取决于其内容，则不应更改节点对象。

在创建完节点后就可以查看节点信息：

G.number_of_nodes()  # 5
G.nodes()  # NodeView((1, 2, 3, 4, 5))

和增加一样，也可以移除节点：

G.remove_node(1)
G.remove_nodes_from([2, 3])

3. 边

图也可以通过一次性增加一条边进行生长，使用add_edge：

G.add_edge(1, 2)
e = (2, 3)
G.add_edge(*e)  # 采用元组解包方式

也可以添加多个边，使用add_edges_from：

G.add_edges_from([(1, 2), (1, 3)])

或者通过添加任何边的ebunch。ebunch是边的元组的任何可迭代容器。边的元组可以是 2 元组节点，也可以是 3 元组：在 2 个节点后跟边的属性字典，如(2, 3,{'weight':3.1415})。

G.add_edges_from([(2, 4, {'weight': 3})])

还有一个方法是add_weighted_edges_from，这个可以指定三元组，第三个元素是边权重：

G = nx.Graph()
G .add_weighted_edges_from([(1, 2, 0.125), (1, 3, 0.75), (2, 4, 1.2), (3, 4, 0.375)])
G[1][2]  # {'weight': 0.125}

边创建好之后，可以查看图的表情况：

G.number_of_edges()  # 4
G.edges()  # EdgeView([(1, 2), (1, 3), (2, 3), (2, 4)])

同样也可以移除边：

G.remove_edge(1, 2)
G.remove_edges_from([(1, 3), (2, 4)])

最后边可以直接在空图中或者还没有建立节点之前创建，如果指定的边的节点不存在图对象中，会先创建出节点：

G = nx.Graph()
G.add_edge(1, 2)
G.nodes  # NodeView((1, 2))，没有提前创建节点，但是直接创建边依旧有节点

添加新的节点/边时，NetworkX 悄悄地忽略任何已经存在的。

G.add_edges_from([(1, 2), (1, 3)])
G.add_node(1)
G.add_edge(1, 2)
G.add_node("spam")        # adds node "spam"
G.add_nodes_from("spam")  # adds 4 nodes: 's', 'p', 'a', 'm'
G.add_edge(3, 'm')

此时，图G 包含 8 个节点和 3 条边：

>>> G.number_of_nodes()
8
>>> G.number_of_edges()
3

邻接报告(adjacency reporting)的顺序（例如，G.adj、G.successors、G.predecessors）是边添加的顺序。 然而，G.edges 的顺序是邻接的顺序，包括节点的顺序和每个节点的邻接。 请参见下面的示例：

DG = nx.DiGraph()
DG.add_edge(2, 1)   # adds the nodes in order 2, 1
DG.add_edge(1, 3)
DG.add_edge(2, 4)
DG.add_edge(1, 2)
assert list(DG.successors(2)) == [1, 4]
assert list(DG.edges) == [(2, 1), (2, 4), (1, 3), (1, 2)]

4. 清空图

使用clear方法清空图

G.clear()

此时在查看图的节点和边属性

G.number_of_nodes()  # 0
G.nodes()  # NodeView(())
G.number_of_edges()  # 0
G.edges()  # EdgeView([])

5. 图可视化

nx.draw_networkx(G)
import matplotlib.pyplot as plt
plt.show()

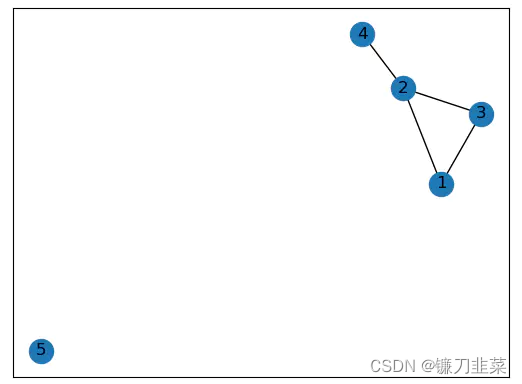
6. 访问图的元素属性

主要是集中在G.nodes, G.edges, G.adj and G.degree四个属性方法，分别查看图的节点，边，邻居（邻接），度的信息，我们来看一下他们的输出结构:

list(G.nodes)  #  [1, 2, 3, 4, 5]，原始输出是NodeView类型
list(G.edges)  # [(1, 2), (1, 3), (2, 3), (2, 4)]，原始输出是EdgeView类型
list(G.adj[1])  # or list(G.neighbors(1))  [2, 3]
G.degree[1]  # the number of edges incident to 1 # 2

如果节点带有属性，想单独访问一个节点的属性，可以在G.nodes后面接节点的下标:

G = nx.Graph()
G.add_node(1, name='gp')
G.add_node(2)
G.nodes[1]  # {'name': 'gp'}

可以指定查询一个或者多个节点的涉及的边:

G.edges([1, 2])  # 所有存在的节点输出边
Out[66]: EdgeDataView([(1, 2), (1, 3), (2, 3), (2, 4)])
G.edges(1)
Out[67]: EdgeDataView([(1, 2), (1, 3)])

另一种访问边的方法是直接对G对象使用下标访问，比如:

G[1]  # 等价于G.adj[1]
Out[75]: AtlasView({2: {}, 3: {}})

如果指定了两个节点，要访问两节点构成的边的属性信息，可以在G.edges中使用直接使用下标属性:

G.edges[2, 4]
Out[87]: {'weight': 3}

等同于直接对G对象做两次节点作为下标的访问：

G[2][4]
Out[91]: {'weight': 3}

同理在构建边的时候，也可以只用这种方式在创建好之后在设置边的属性：

G = nx.Graph()
G.add_node(1)
G.add_node(2)
G.add_edge(1, 2)
G[1][2]['color'] = 'red'
G[1][2]['weight'] = 3
G[1]  # AtlasView({2: {'color': 'red', 'weight': 3}})

如果要对全部边进行访问，不仅访问边的节点，而且还要访问边的属性，使用G.edges.data()方法，比如：

G = nx.Graph()
G.add_weighted_edges_from([(1, 2, 0.125), (1, 3, 0.75), (2, 4, 1.2), (3, 4, 0.375)])
for (u, v, wt) in G.edges.data():
    print(u, v, wt)
# 1 2 {'weight': 0.125}
# 1 3 {'weight': 0.75}
# 2 4 {'weight': 1.2}
# 3 4 {'weight': 0.375}

G.adj是一个多层嵌套字典的格式，记录每个点的近邻，以及近邻的属性:

G.adj
Out[40]: AdjacencyView({1: {2: {}, 3: {}}, 2: {1: {}, 3: {}, 4: {'weight': 3}}, 3: {2: {}, 1: {}}, 4: {2: {'weight': 3}}, 5: {}})

比如指定节点2的近邻，分别有1,3,4，并且4有属性边权:

G.adj[2]
Out[41]: AtlasView({1: {}, 3: {}, 4: {'weight': 3}})

也可以直接对G对象使用节点下标，作用等同于在找近邻:

G = nx.Graph()
G.add_node(1, name='gp')
G.add_node(2)
G.add_edge(1, 2)
G[2]  # AtlasView({1: {}})
G.adj[2]  # AtlasView({1: {}})

如果仅要输出近邻节点的列表:

list(G.adj[2])  # [1, 3, 4]

可以将AtlasView作为字典循环迭代出来:

for i, j in G.adj.items():
    print(i, j)
# 1 {2: {}, 3: {}}
# 2 {1: {}, 3: {}, 4: {'weight': 3}}
# 3 {2: {}, 1: {}}
# 4 {2: {'weight': 3}}
# 5 {}

查看近邻也可以使用neighbors方法，指定一个节点：

G.neighbors(2)  # <dict_keyiterator at 0x7fb864efb410>
list(G.neighbors(2))  # [1, 3, 4]

最后是查看节点的度，结构依旧是个字典：

G.degree
Out[47]: DegreeView({1: 2, 2: 3, 3: 2, 4: 1, 5: 0})

如果要访问某个节点的度，使用字典的key访问，无向图的度不分出入：

G.degree[2]  # 3

度默认边出现一次权重是1，如果本身手动指定了权重，在degree方法中增加weight=‘weight’，其中weight是自动的权重的key值：

G = nx.Graph()
G.add_weighted_edges_from([(1, 2, 0.25)])
G.degree(1, weight='weight')  # 0.25

或者：

G = nx.Graph()
G.add_edge(1, 2)
G[1][2]['wt'] = 0.25
G.degree(1, weight='wt') 

直接指定节点，获取节点的度：

G.degree[1]
Out[48]: 2

也可以指定多个节点，返回存在节点的度：

G.degree([2, 3])
Out[54]: DegreeView({2: 3, 3: 2})

7. 向图、节点或边种添加属性

可以向图，以及节点和边中添加类似颜色，权重，标签甚至任何Python对象的属性，比如对图对象，可以在创建的时候就指定属性，也可以创建完成之后增加：

G = nx.Graph(name='gp')
G.graph  #  {'name': 'gp'}
G2 = nx.Graph()
G2.graph['name'] = 'gp'
G.graph  # {'name': 'gp'}

同样对于节点node也有对应的API进行属性赋值和增加add_node，add_nodes_from，G.nodes：

G = nx.Graph()
G.add_node(1)
G.nodes[1]['name'] = 'gp'
G.nodes.data()  # NodeDataView({1: {'name': 'gp'}})

在节点初始化的时候就创建：

G.add_nodes_from([1, 2], name='gp')  # 多个节点相同属性
G.add_node(1, name='gp')  # 单个节点创建属性

同理对于边也是这样操作：

G.add_edge(1, 2, weight=4.7 )
G.add_edges_from([(3, 4), (4, 5)], color='red')
G.add_edges_from([(1, 2, {'color': 'blue'}), (2, 3, {'weight': 8})])
G[1][2]['weight'] = 4.7
G.edges[3, 4]['weight'] = 4.2

8. 有向图

有向图使用nx.DiGraph，在有向图中，degree分为out_degree和in_degree，两者的和等于degree，近邻分为前驱predecessors和后继successors:

DG = nx.DiGraph()
DG.add_weighted_edges_from([(1, 2, 0.5), (3, 1, 0.75)])

查看节点1的近邻，发现只有2没有3，说明是从元组的第一个元素向第二个元素:

DG[1]  # AtlasView({2: {'weight': 0.5}})

查看度，出度和入度：

DG.degree(1)  # 2
DG.in_degree(1)  # 1
DG.out_degree(1)  # 1

有向图的neighbors和successors结果一致，近邻就是后继，不算前驱：

DG = nx.DiGraph()
DG.add_weighted_edges_from([(1, 2, 0.5), (3, 1, 0.75)])
list(DG.neighbors(1))  # [2]
list(DG.successors(1))  # [2]
list(DG.predecessors(1))  # [3]

有向图可以转化为无向图，使用to_undirected，或者将有向图对象传给无向图:

DG = nx.DiGraph()
DG.add_weighted_edges_from([(1, 2, 0.5), (3, 1, 0.75)])
G = DG.to_undirected()
list(G.neighbors(1))  # [2, 3]

或者:

DG = nx.DiGraph()
DG.add_weighted_edges_from([(1, 2, 0.5), (3, 1, 0.75)])
G = nx.Graph(DG)
list(G.neighbors(1))  # [2, 3]

9. 画出复杂网络

NetworkX不是一个图形绘图软件包，而是一个带有Matplotlib的基本绘图软件包，以及一个使用开源Graphviz软件包的接口，画图首先要导入matplotlib，然后draw_networkx G对象，常用画图参数如下:

import matplotlib.pyplot as plt
G = nx.Graph()
G.add_edges_from([(2, 4), (2, 3), (2, 1), (1, 3)])
G.add_node(5)
options = {
    'node_color': 'green',  # 节点颜色
    'node_size': 1200,  # 节点大小
    'width': 1,  # 边粗
    'alpha': 0.7,  # 节点颜色透明度
    'linewidths': 2,  # 节点边缘线粗细
    'edge_color': 'green',  # 边颜色
    'style': 'dashed',  # 边的线型，默认实线，改为虚线
    'font_size': 13,  # 节点上标签的字体大小
    'font_color': 'white'  # 节点上标签字的颜色
}
nx.draw_networkx(G, **options)
plt.show()

输出效果：

进一步可以保存图到本地为图片格式文件：

plt.savefig("./path.png")

10.图结构持久化和从外部文件读取图数据

将图结构保存为pickle格式，使用write_gpickle，读取pickle格式图结构使用read_gpickle：

G = nx.Graph()
G.add_edges_from([(2, 4), (2, 3), (2, 1), (1, 3)])
G.add_node(5)
nx.write_gpickle(G, "./graph.pkl")

G2 = nx.read_gpickle("./graph.pkl")
G2.nodes  # NodeView((2, 4, 3, 1, 5))

另外也可以存储为txt文件格式，比如edgelist和adjlist格式:

G = nx.Graph()
G.add_weighted_edges_from([(2, 4, 3), (2, 3, 2), (2, 1, 1), (1, 3, 5)])
nx.write_edgelist(G, "graph.edgelist")
G2 = nx.read_edgelist("graph.edgelist")
G2.edges.data()  # EdgeDataView([('2', '4', {'weight': 3}), ('2', '3', {'weight': 2}), ('2', '1', {'weight': 1}), ('3', '1', {'weight': 5})])

查看保存的数据，结果是空格分隔符的三元素，第三个元素是属性字典，第一第二是两个互相连接节点：

2 4 {'weight': 3}
2 3 {'weight': 2}
2 1 {'weight': 1}
3 1 {'weight': 5}

再试一下adjlist格式：

G = nx.Graph()
G.add_edges_from([(2, 4), (2, 3), (2, 1), (1, 3)])
nx.write_adjlist(G, "./graph.adjlist")
G2 = nx.read_adjlist("./graph.adjlist")

查看adjlist格式结果，adjlist是由头元素+尾序列组成的，头元素和尾序列的每一个作为边的两边的节点，不论adjlist还是edgelist，所有节点对都只算1次，交换位置不重复记录，但是在读取的时候可以自由转为有向图和无向图:

2 4 3 1
4
3 1
1

默认读取是Graph无向图，如果要读取成有向图，在read方法中指定参数create_using=nx.DiGraph:

G = nx.DiGraph()
G.add_edges_from([(2, 4), (2, 3), (2, 1), (1, 3)])
nx.write_adjlist(G, "./graph.adjlist")
G2 = nx.read_adjlist("./graph.adjlist")
list(G2.neighbors('1'))  # ['2', '3']
G3 = nx.read_adjlist("./graph.adjlist", create_using=nx.DiGraph)
list(G3.neighbors('1'))  # ['3']

需要注意的是如果保存文件的时候节点是数值对象，读进来之后节点都会自动转化为字符串，如果要指定节点数据类型，需要在read方法中增加参数比如nodetype=int：

G2 = nx.read_adjlist("./graph.adjlist", nodetype=int)
list(G2.neighbors(1))  # ['2', '3']

11. 多图

NetworkX 提供了允许任意一对节点之间存在多条边的图类。 MultiGraph 和 MultiDiGraph 类允许您添加相同的边两次，可能使用不同的边数据。 这对于某些应用程序来说可能很强大，但许多算法在此类图上没有很好地定义。 在结果定义明确的地方，例如 MultiGraph.degree() 我们提供了函数。 否则，您应该以使测量明确定义的方式转换为标准图表。

MG = nx.MultiGraph()
MG.add_weighted_edges_from([(1,2,0.5),(1,2,0.75),(2,3,0.5)])
dict(MG.degree(weight='weight'))  
# {1: 1.25, 2: 1.75, 3: 0.5}
GG = nx.Graph()
for n, nbrs in MG.adjacency():
    for nbr, edict in nbrs.items():
        minvalue = min([d['weight'] for d in edict.values()])
        GG.add_edge(n, nbr, weight=minvalue)
nx.shortest_path(GG, 1,3)
# [1, 2, 3]

参考资料

[1] 图论的基本理论
[2] Network Tutorial
[3] 复杂网络基础知识以及Networkx官方文档学习使用