本篇博客介绍了使用射线法判断点在多边形内部还是外部的算法，并通过C++做了具体实现

1. 算法思路

判断平面内点是否在多边形内有多种算法，其中射线法是其中比较好理解的一种，而且能够支持凹多边形的情况。该算法的思路很简单，就是从目标点出发引一条射线，看这条射线和多边形所有边的交点数目。如果有奇数个交点，则说明在内部，如果有偶数个交点，则说明在外部。

如下图所示：射线和多边形一共有5个交点，为奇数，所以点在多边形内

2. 算法步骤

  2.1 已知点point(x,y)和多边形Polygon的点有序集合（x1,y1;x2,y2;….xn,yn;）；
以point为起点，以无穷远为终点作平行于X轴的射线line(x,y; -∞,y)；循环取得多边形的每一条边side(xi,yi;xi+1,yi+1)：
  2.2. 判断point(x,y)是否在side上，如果是，则返回true。
  2.3. 判断line与side是否有交点，如果有则count++。判断交点的总数count，如果为奇数则返回true，偶数则返回false。

2.4 判断交点的总数count，如果为奇数则返回true，偶数则返回false。

极端情况需要注意：当射线line经过的是多边形的顶点时，判断就会出现异常情况。针对这个问题，由于多边形的每一个顶点都在两个线段上，可以根据线段的两个端点的y坐标做上下判断，y值较大的顶点称为上端点，y值较小是下端点。如果射线经过上端点，count加1，如果经过下端点，则count不必加1，如下图

第一个图，交叉点为X，先计算线段(p1,p2)，由于经过的是p2,即下端点，count值不加；再计算线段(p2,p3)，由于经过的是p2,也是下端点，count值还是不加，总结：射线和 多边形一共有1个交点，为奇数，所以A在多边形内

第二个图，交叉点为X，先计算线段(p1,p2)，由于经过的是p2,即上端点，count值加1；再计算线段(p2,p3)，由于经过的是p2,也是上端点，count值加1，总结：射线和 多边形一共有3个交点，为奇数，所以A在多边形内

 3. 实现代码

#include<iostream>
#include <cmath>
#include <vector>
#include <algorithm>
using namespace std;

// 浮点数最小精度
#define EPSILON 0.000001

// 向量（也可用来表点）
struct  Vec2d
{
	double x, y;

	Vec2d()
	{
		x = 0.0;
		y = 0.0;
	}
	Vec2d(double dx, double dy)
	{
		x = dx;
		y = dy;
	}
	void Set(double dx, double dy)
	{
		x = dx;
		y = dy;
	}
};

// 判断点在线段上
// (px0, py0)	:	点坐标
// (px1, py1)	:	边的第一个点
// (px2,py2)	:	边的第二个点
bool IsPointOnLine(double px0, double py0, double px1, double py1, double px2, double py2)
{
	bool flag = false;
	double d1 = (px1 - px0) * (py2 - py0) - (px2 - px0) * (py1 - py0);
	if ((abs(d1) < EPSILON) && ((px0 - px1) * (px0 - px2) <= 0) && ((py0 - py1) * (py0 - py2) <= 0))
	{
		flag = true;
	}
	return flag;
}

// 判断两线段相交
// (px1, py1)	:	第一边的第一个点
// (px2, py2)	:	第一边的第二个点
// (px3, py3)	:	第二边的第一个点
// (px4, py4)	:	第二边的第二个点
bool IsIntersect(double px1, double py1, double px2, double py2, double px3, double py3, double px4, double py4)
{
	bool flag = false;
	double d = (px2 - px1) * (py4 - py3) - (py2 - py1) * (px4 - px3);
	if (d != 0)
	{
		double r = ((py1 - py3) * (px4 - px3) - (px1 - px3) * (py4 - py3)) / d;
		double s = ((py1 - py3) * (px2 - px1) - (px1 - px3) * (py2 - py1)) / d;
		if ((r >= 0) && (r <= 1) && (s >= 0) && (s <= 1))
		{
			flag = true;
		}
	}
	return flag;
}

// 判断点是否在多边形内(点在多边形的边上也算在内部)
// (x, y)	:	点坐标
// POL		:	多边形的各个点（需连续，顺时针/逆时针皆可）
bool Point_In_Polygon_2D(double x, double y, const vector<Vec2d>& POL)
{
	bool isInside = false;
	int  count    = 0;

	// 求出多边形的最小X
	double minX = DBL_MAX;
	for (int i=0; i<POL.size(); i++)
	{
		minX = std::min(minX, POL[i].x);
	}

	double px = x;
	double py = y;

	// 负X方向的水平射线，(x,y)做起点，(minX, y)做终点
	double linePoint1x = x;
	double linePoint1y = y;
	double linePoint2x = minX - 10;			
	double linePoint2y = y;

	// 遍历每一条边
	for (int i = 0; i < POL.size()-1; i++)
	{
		double cx1 = POL[i].x;	// 多边形的第i个点
		double cy1 = POL[i].y;		
		double cx2 = POL[i+1].x;// 多边形的第i+1个点
		double cy2 = POL[i+1].y;

		// 点在多边形上，算是在内部
		if (IsPointOnLine(px, py, cx1, cy1, cx2, cy2))
		{
			return true;
		}

		// X方向水平的边，不用计算，肯定不会和射线相交
		if (fabs(cy2 - cy1) < EPSILON)
		{
			continue;
		}

		// 多边形的一个顶点在射线上，且该顶点是上顶点(y值较高)，算一个交点
		if (IsPointOnLine(cx1, cy1, linePoint1x, linePoint1y, linePoint2x, linePoint2y))
		{
			if (cy1 > cy2)
			{
				count++;
			}
		}
		// 多边形的一个顶点在射线上，且该顶点是上顶点(y值较高)，算一个交点
		else if (IsPointOnLine(cx2, cy2, linePoint1x, linePoint1y, linePoint2x, linePoint2y))
		{
			if (cy2 > cy1)
			{
				count++;
			}
		}
		// 已经排除平行的情况，其他相交的都算一个交点
		else if (IsIntersect(cx1, cy1, cx2, cy2, linePoint1x, linePoint1y, linePoint2x, linePoint2y))   
		{
			count++;
		}
	}

	// 交点数为奇数，则在多边形内，反之在多边形外
	if (count % 2 == 1)
	{
		isInside = true;
	}

	return isInside;
}


int main()
{
	//定义一个多边形（六边形）
	vector<Vec2d> POL;
	POL.push_back(Vec2d(268.28, 784.75));
	POL.push_back(Vec2d(153.98, 600.60));
	POL.push_back(Vec2d(274.63, 336.02));
	POL.push_back(Vec2d(623.88, 401.64));
	POL.push_back(Vec2d(676.80, 634.47));
	POL.push_back(Vec2d(530.75, 822.85));
	POL.push_back(Vec2d(268.28, 784.75));				//将起始点放入尾部，方便遍历每一条边

	//
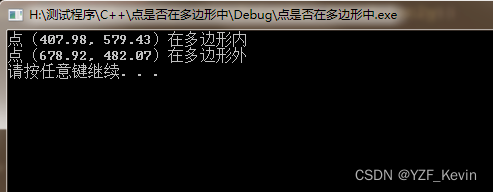
	if (Point_In_Polygon_2D(407.98, 579.43, POL))
	{
		cout << "点（407.98, 579.43）在多边形内" << endl;
	}
	else
	{
		cout << "点（407.98, 579.43）在多边形外" << endl;
	}

	//
	if (Point_In_Polygon_2D(678.92, 482.07, POL))
	{
		cout << "点（678.92, 482.07）在多边形内" << endl;
	}
	else
	{
		cout << "点（678.92, 482.07）在多边形外" << endl;
	}

	system("pause");
	return 0;
}

4. 执行结果