62. 不同路径

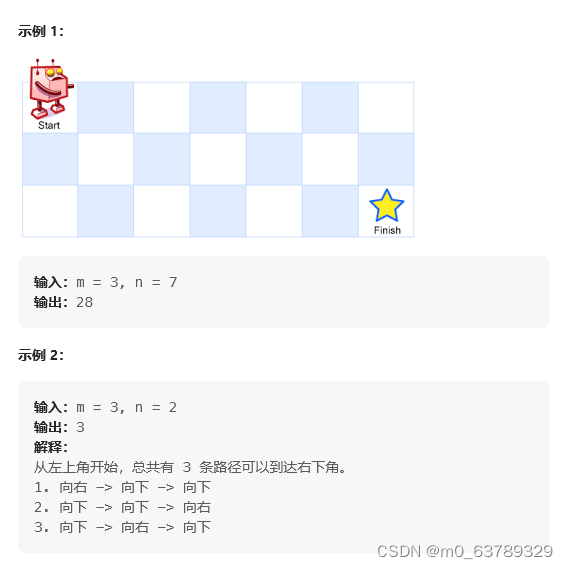
1. dp数组以及下标名义

dp[i][j]:表示从（0 ，0）出发，到达坐标（i,j）位置路径数

2. 递归公式

dp[i][j] = dp[i][j - 1] + dp[i - 1][j];

3. dp数组如何初始化

首先dp[i][0]一定都是1，因为从(0, 0)的位置到(i, 0)的路径只有一条，那么dp[0][j]也同理

       for(int i = 1; i < n; i++) {
           dp[0][i] = 1;
       }
        for(int j = 1; j < m; j++) {
           dp[j][0] = 1;

4. 遍历顺序

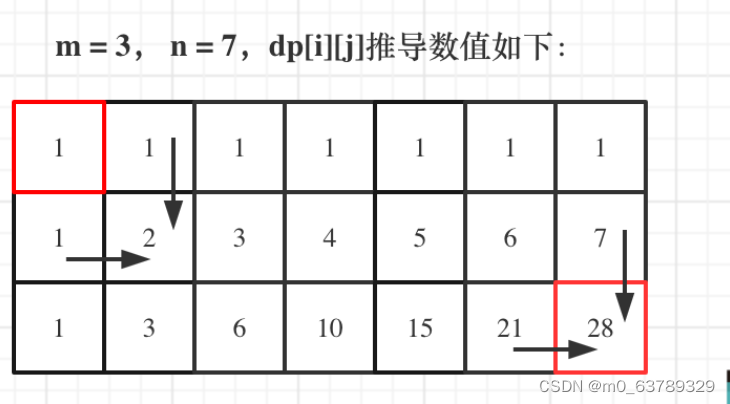
5.代码

class Solution {
public:
    int uniquePaths(int m, int n) {
       if(m == 0&&n == 0)return 0;
       if( m == 1 && n == 1)return 1;
        vector<vector<int>>dp(m + 1,vector<int>(n + 1));
       for(int i = 1; i < n; i++) {
           dp[0][i] = 1;
       }
        for(int j = 1; j < m; j++) {
           dp[j][0] = 1;
       }
        for( int i = 1; i < m; i++) {
             for( int j = 1; j < n; j++) {
                 dp[i][j] = dp[i][j - 1] + dp[i - 1][j];
                 cout<<i<<","<<j<<":"<<dp[i][j]<<endl;
             }
        }
        return dp[m - 1][n - 1];

    }
};

63. 不同路径 II：有障碍物

1. dp数组以及下标名义

dp[i][j] ：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。

2. 递归公式

递推公式和62.不同路径一样，dp[i][j] = dp[i - 1][j] + dp[i][j - 1]

3. dp数组如何初始化:没有障碍时，第一行和第一列为1，遇到障碍后所有都为0，因为本身定义数组初始为0的所有不用管它

与上一题不同

vector<vector<int>>dp(m + 1,vector<int>(n + 1,0));
          for(int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {
             dp[i][0] = 1;
       }
         for(int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
             dp[0][j] = 1;
       }

4. 遍历顺序（从左到右一层一层遍历，遇到障碍跳过）

for (int i = 1; i < m; i++) {
    for (int j = 1; j < n; j++) {
        if (obstacleGrid[i][j] == 1) continue;
        dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
    }
}

5.代码

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
        //如果起点或者终点有障碍，直接返回0
       if(obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) return 0 ;
        vector<vector<int>>dp(m + 1,vector<int>(n + 1,0));
          for(int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {
             dp[i][0] = 1;
       }
         for(int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
             dp[0][j] = 1;
       }
       for( int i = 1; i < obstacleGrid.size(); i++) {
             for( int j = 1; j < obstacleGrid[0].size(); j++) {
                 if(obstacleGrid[i][j] ) continue; //有障碍时continue
                    dp[i][j] = dp[i][j - 1] + dp[i - 1][j];                    
                 }
             }
        return dp[obstacleGrid.size() - 1][obstacleGrid[0].size() - 1];
    }
};