343. 整数拆分

1. dp数组以及下标名义

dp[i]：分拆数字i，可以得到的最大乘积为dp[i]。

2. 递归公式

1.dp[i]的乘积如何得到：一种是j*(i - j)直接相乘；二种是jdp[i - j],拆分（i - j）
递推公式：dp[i] = max(j(i - j) , j*dp[i - j])
dp[i] = max(dp[i],max((i - j)*j,dp[i - j]*j))

3. dp数组如何初始化

4. 遍历顺序:遍历i是从前向后遍历，先有dp[i - j]再有dp[i]

5. 代码

class Solution {
public:
    int integerBreak(int n) {
        vector<int>dp(n + 1);
        if(n == 0 || n == 1) return 0;
        dp[1] = 0; dp[2] = 1;
        for(int i = 3; i <= n; i++) {
            for(int j = 1; j < i - 1; j++) {
                dp[i] = max(dp[i],max((i - j)*j,dp[i - j]*j));
            }
        }
        return dp[n];
    }
};

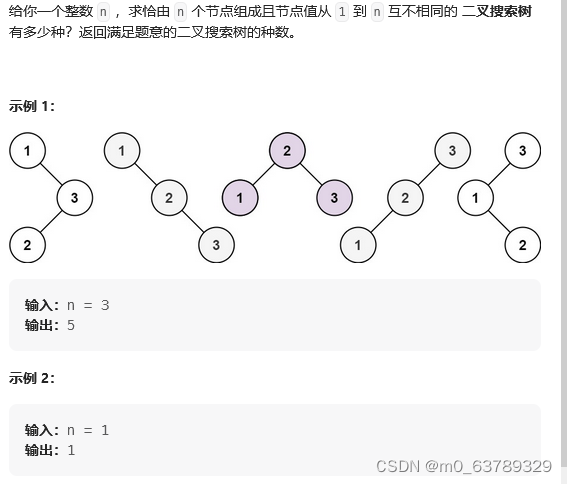
96.不同的二叉搜索树

1. dp数组以及下标名义

dp[i]:表示1到 i 为节点组成的二叉搜索树个数

2. 递归公式

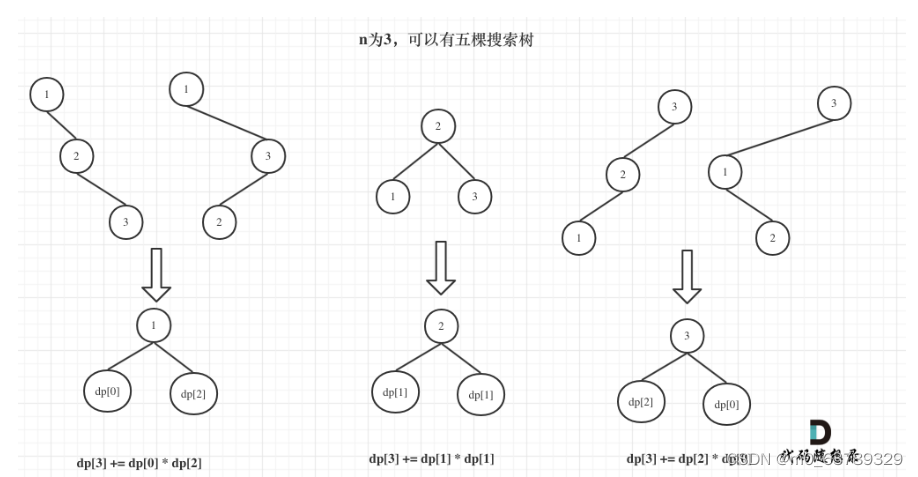dp[3]，就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
元素1为头结点搜索树的数量 =右子树有2个元素的数量左子树有0个元素的数量
元素2为头结点搜索树的数量 =右子树有1个元素的数量左子树有1个元素的数量
元素3为头结点搜索树的数量 =左子树有2个元素的数量*右子树有0个元素的数量
有2个元素的搜索树数量就是dp[2]。

有1个元素的搜索树数量就是dp[1]。

有0个元素的搜索树数量就是dp[0]。

所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
dp[i] += dp[j - 1] * dp[i - j]

3. dp数组如何初始化

初始化，只需要初始化dp[0]就可以了，推导的基础，都是dp[0]；初始化dp[0] = 1因为空节点也是一棵二叉树

4. 遍历顺序

首先一定是遍历节点数，从递归公式：dp[i] += dp[j - 1] * dp[i - j]可以看出，节点数为i的状态是依靠 i之前节点数的状态。

那么遍历i里面每一个数作为头结点的状态，用j来遍历。

5. 代码

class Solution {
public:
    int numTrees(int n) {
        vector<int>dp(n + 1);
        dp[0] = 1;
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= i; j++) {
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        return dp[n];
    }
};