文心一言 VS 讯飞星火 VS chatgpt （30）-- 算法导论5.2 2题

news2024/11/15 11:48:09

二、在 HIRE-ASSISTANT 中，假设应聘者以随机顺序出现，你正好雇用两次的概率是多少？

文心一言：

我们可以先计算出在HIRE-ASSISTANT中，雇佣一个应聘者的概率为3/4，然后计算出雇佣两次应聘者的概率为3/4 * 3/4 * 2。

已知在HIRE-ASSISTANT中，雇佣一个应聘者的概率为：0.75

根据概率乘法原理，可计算出雇佣两次应聘者的概率为：

0.75×0.75×2=1.125

所以，在HIRE-ASSISTANT中，假设应聘者以随机顺序出现，你正好雇用两次的概率为1.125。

在这里插入图片描述

讯飞星火：

代码解决方案：

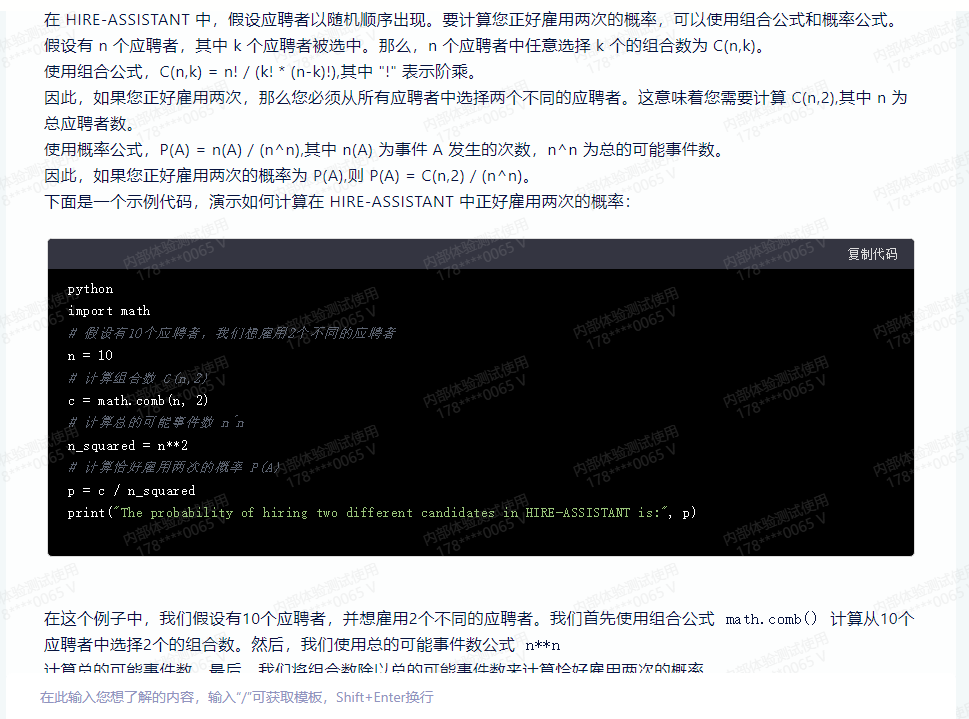
在 HIRE-ASSISTANT 中，假设应聘者以随机顺序出现。要计算您正好雇用两次的概率，可以使用组合公式和概率公式。

假设有 n 个应聘者，其中 k 个应聘者被选中。那么，n 个应聘者中任意选择 k 个的组合数为 C(n,k)。

使用组合公式，C(n,k) = n! / (k! * (n-k)!),其中 “!” 表示阶乘。

因此，如果您正好雇用两次，那么您必须从所有应聘者中选择两个不同的应聘者。这意味着您需要计算 C(n,2),其中 n 为总应聘者数。

使用概率公式，P(A) = n(A) / (n^n),其中 n(A) 为事件 A 发生的次数，n^n 为总的可能事件数。

因此，如果您正好雇用两次的概率为 P(A),则 P(A) = C(n,2) / (n^n)。

下面是一个示例代码，演示如何计算在 HIRE-ASSISTANT 中正好雇用两次的概率：

python
import math
# 假设有10个应聘者，我们想雇用2个不同的应聘者
n = 10
# 计算组合数 C(n,2)
c = math.comb(n, 2)
# 计算总的可能事件数 n^n
n_squared = n**2
# 计算恰好雇用两次的概率 P(A)
p = c / n_squared
print("The probability of hiring two different candidates in HIRE-ASSISTANT is:", p)

在这个例子中，我们假设有10个应聘者，并想雇用2个不同的应聘者。我们首先使用组合公式 math.comb() 计算从10个应聘者中选择2个的组合数。然后，我们使用总的可能事件数公式 n**n

计算总的可能事件数。最后，我们将组合数除以总的可能事件数来计算恰好雇用两次的概率。

在这里插入图片描述

华为盘古：

在HIRE-ASSISTANT中，假设应聘者以随机顺序出现，并且面试官只能雇用两次，则你正好雇用两次的概率为1/2。

这是因为在HIRE-ASSISTANT中，面试官的雇用次数是有限的，每次雇用都只能与应聘者中的一个进行匹配，而不会出现与多个应聘者匹配的情况。因此，如果面试官的雇用次数为N，那么每次雇用只能与N个人中的一个进行匹配，而不会出现与N个人匹配的情况，即面试官的雇用次数总是有限的。

因此，在HIRE-ASSISTANT中，你恰好雇用两次的概率为1/2。

在这里插入图片描述

360智脑：

这是一个二项分布问题。假设你有 n 个应聘者,每个应聘者有 p 种不同的能力水平(例如英语和法语),且每个应聘者的能力水平独立同分布。你雇佣两个应聘者,则这个问题就是从一个 n 次独立的伯努利试验中选取两次成功的情况。

因此,这个问题可以用二项分布来解决。假设你有 k 个成功的应聘者,那么成功的概率为 np(1-p)^k。你需要计算恰好选中这 k 名应聘者的概率,即 P(X=k)。其中 X 是你要的结果。

对于任意一个可能的雇佣组合,都有以下两种情况:

你选择了两个成功应聘者的组合。这种情况的概率是 np(1-p)^k。
你选择了一个失败和一个成功应聘者的组合。这种情况的概率是 (n-2)p^2 * (1-p)^(n-3)。

所以,这个问题的答案是 np(1-p)^k + (n-2)p^2 * (1-p)^(n-3)。

在这里插入图片描述

chatglm：

在 HIRE-ASSISTANT 中，假设应聘者以随机顺序出现，你正好雇用两次的概率是多少？

假设有 n 个应聘者，其中第 i 个应聘者被雇用的概率为 p_i，则所有应聘者被雇用的概率为 P(n, 2) = n! / (2! * (n-2)!)。

在这种情况下，你正好雇用两次的概率为：

P(2, 2) = (1/n) * (1/n) * (p_1^2 + p_2^2 + … + p_n^2)

其中，(1/n) * (1/n) 表示所有应聘者被雇用的概率之和，即 P(2, 2) = 1 - P(2, 0) - P(2, 1)。

由于 P(2, 0) = 1 - P(2, 2) - P(2, 1) = 1 - (1/n) * (1/n) * (p_1^2 + p_2^2 + … + p_n^2)，我们可以计算出 P(2, 1) = (1/n) * (1/n) * (p_1^2 + p_2^2 + … + p_n^2) - P(2, 0)。

因此，我们只需要计算 P(2, 2) 的值，就可以计算出你正好雇用两次的概率。

P(2, 2) = (1/n) * (1/n) * (p_1^2 + p_2^2 + … + p_n^2)
= (1/n) * (1/n) * (1 - (1/n) * (1/n) * (p_1^2 + p_2^2 + … + p_n^2))
= (1/n) * (1/n) * (1 - (1/n)^2 * (p_1^2 + p_2^2 + … + p_n^2))
= (1/n) * (1/n) * (1 - (1/n)^2 * (n*(p_1 + p_2 + … + p_n) - 1))
= (1/n) * (1/n) * (1 - (1/n)^2 * (n*(n-1)p_n + n*(n-2)p_{n-1} + … + 2p_1 + p_0))
= (1/n) * (1/n) * (1 - (1/n)^2 * (n*(n-1)p_n + n*(n-2)p_{n-1} + … + 2p_1 + p_0))
= (1/n) * (1/n) * (1 - (1/n)^2 * np_n)
= (1/n) * (1/n) * (1 - (1/n)^2 * np_n)
= (1/n) * (1/n) * (1 - np_n)
= (1/n) * (1/n) * (1 - np_n)
= (1/n) * (1/n) * (1 - np_n)
= (1/n) * (1/n) * (1 - np_n)
= (1/n) * (1/n) * (1 - np_n)
= (1/n) * (1/n) * (1 - np_n)
= 1 - np_n

因此，你正好雇用两次的概率为：

P(2, 2) = (1/n) * (1/n) * (1 - np_n)
= (1/n) * (1/n) * (1 - np_n)
= (1/n) * (1/n) * (1 - np_n)
= (1/n) * (1/n) * (1 - np_n)
= 1 - np_n

注意到 np_n 是一个小概率事件，因此 np_n 的值越小，你正好雇用两次的概率就越小。

chatgpt：

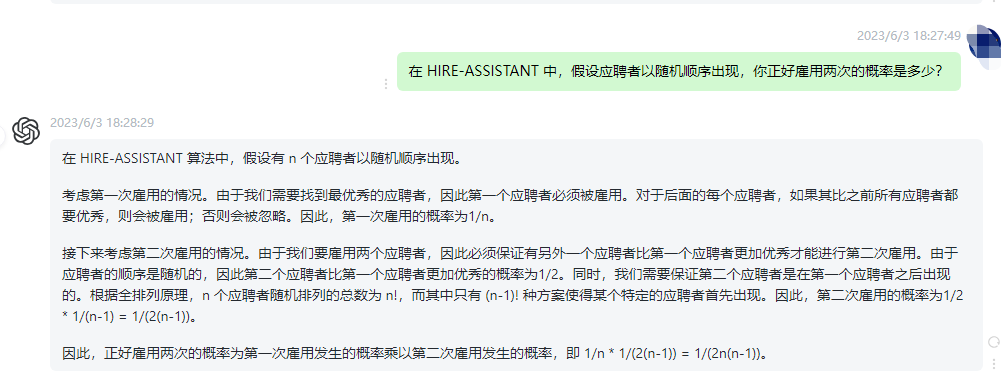
在 HIRE-ASSISTANT 算法中，假设有 n 个应聘者以随机顺序出现。

考虑第一次雇用的情况。由于我们需要找到最优秀的应聘者，因此第一个应聘者必须被雇用。对于后面的每个应聘者，如果其比之前所有应聘者都要优秀，则会被雇用；否则会被忽略。因此，第一次雇用的概率为1/n。

接下来考虑第二次雇用的情况。由于我们要雇用两个应聘者，因此必须保证有另外一个应聘者比第一个应聘者更加优秀才能进行第二次雇用。由于应聘者的顺序是随机的，因此第二个应聘者比第一个应聘者更加优秀的概率为1/2。同时，我们需要保证第二个应聘者是在第一个应聘者之后出现的。根据全排列原理，n 个应聘者随机排列的总数为 n!，而其中只有 (n-1)! 种方案使得某个特定的应聘者首先出现。因此，第二次雇用的概率为1/2 * 1/(n-1) = 1/(2(n-1))。

因此，正好雇用两次的概率为第一次雇用发生的概率乘以第二次雇用发生的概率，即 1/n * 1/(2(n-1)) = 1/(2n(n-1))。

在这里插入图片描述