1柔性车间作业调度
-
n n n个工件 { J 1 , J 2 , ⋯ , J n } \{J_1,J_2,\cdots,J_n\} {J1,J2,⋯,Jn}要在 m m m台机器 { M 1 , M 2 , ⋯ , M m } \{M_1,M_2,\cdots,M_m\} {M1,M2,⋯,Mm}上加工。每个工件包含一道或多道工序,工序顺序是预先确定的,每道工序可以在多台不同加工机器上进行加工,工序的加工时间随加工机器的不同而不同。调度目标是为每道工序选择最合适的机器、确定每台机器上各个工序的最佳加工顺序以及开工时间,使整个系统 的某些性能指标达到最优。因此柔性作业车间调度问题包含两个子问题确定各工件的加工机器机器选择子问 和确定各个机器上的加工先后顺序工序排序子问题。
-
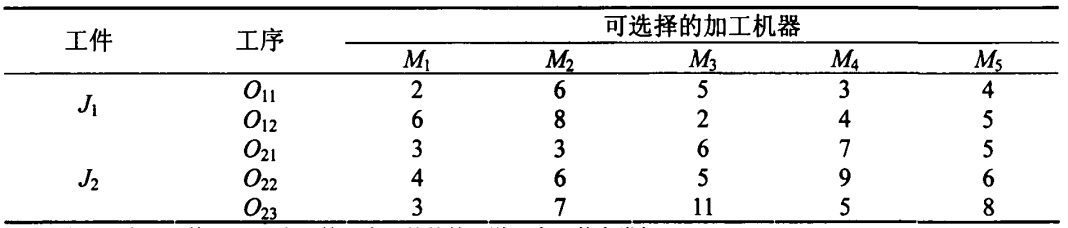
柔性作业车间调度问题根据资源选择条件的不同,柔性程度可以分为完全柔性作业车间调度问题(T-FJSP,工序可选择的加工机器为所有候选机器)和部分柔性作业车间调度问题(P-FJSP,工序可选择的加工机器为部分候选机器)。具体示例如下:

1.1问题背景
现有多个job分属不同产品,每个job对应多个工序,工序可在多台机器上加工,同一个job的工序有先后之分,不同job的工序之间无顺序要求。此外,在任意一台设备上,当连续出现前后多个工序所属job的产品型号相同,且无间隔时间时,这些工序可合并生产,加工时间降低25%。
1.2模型假设
- 同一台机器同一时刻只能加工一个工件
- 同一工件的同一道工序在同一时刻只能被一台机器加工
- 每个工件的每道工序一旦开始加工不能中断
- 不同工件之间具有相同的优先级
- 不同工件的工序之间没有先后约束
- 同一工件的工序之间有先后约束
- 所有工件在零时刻都可以被加工。
1.3符号释义
| 索引符号 | 含义 |
|---|---|
| i , h i,h i,h | 工件索引 ( 1 , … , n ) (1,…,n) (1,…,n) |
| j , g j,g j,g | 工序索引 ( 1 , . . . , J i ) (1,...,J_i) (1,...,Ji) |
| k k k | 机器索引 ( 1 , … , m ) (1,…,m) (1,…,m) |
| l , z l,z l,z | 工序在机器 k k k上的加工顺序 ( 1 , … , d k ) (1,…,d_k) (1,…,dk) |
| 参数符号 | 含义 |
|---|---|
| n n n | 总的工件数 |
| m m m | 总的机器数 |
| J i J_i Ji | 工件 i i i的工序数 |
| a k i j a_{kij} akij | 0-1变量,如果工序 O i j O_{ij} Oij能够在机器 k k k上加工则 a k i j = 1 a_{kij}=1 akij=1,否则 a k i j = 0 a_{kij}=0 akij=0 |
| p k i j p_{kij} pkij | 机器 k k k加工工序 O i j O_{ij} Oij的加工时间 |
| M M M | 一个足够大的正数 |
| O i j O_{ij} Oij | 表示工件 i i i的第 j j j道工序 |
| p t i pt_i pti | 工件 i i i所属产品类型 |
| 变量符号 | 含义 |
|---|---|
| C m a x C_{max} Cmax | 最大完工时间 |
| c i j c_{ij} cij | 工序 O i j O_{ij} Oij的完工时间 |
| s i j k s_{ijk} sijk | 工序 O i j O_{ij} Oij在机器 k k k上的开始加工时间 |
| c i j k c_{ijk} cijk | 工序 O i j O_{ij} Oij在机器 k k k上的加工完成时间 |
| c i c_i ci | 工件 i i i的加工完成时间 |
| x i j k l x_{ijkl} xijkl | 0-1变量,如果 O i , j O_{i,j} Oi,j为机器 k k k加工的第 l l l个工序则为1,否则为0 |
| v i j k v_{ijk} vijk | 0-1变量,如果 O i , j O_{i,j} Oi,j在机器 k k k上加工 |
| t i j t_{ij} tij | O i j O_{ij} Oij的开始加工时间 |
| T m s k l Tms_{kl} Tmskl | 机器 k k k加工第 l l l道工序的开始加工时间 |
| T m e k l Tme_{kl} Tmekl | 机器 k k k加工第 l l l道工序的加工完成时间 |
| p s i , j ps_{i,j} psi,j | O i , j O_{i,j} Oi,j选择在机器 k k k上加工的理论加工时间 |
| a p s i , j aps_{i,j} apsi,j | O j , h O_{j,h} Oj,h的实际加工时间 |
| p t i pt_i pti | 工件 i i i所属产品类型 |
1.4数学模型
目标函数:最小化最大完工时间
min
C
m
a
x
\text{min} \quad C_{max}
minCmax
C
m
a
x
≥
t
i
,
J
i
+
a
p
s
i
,
J
i
∀
i
C_{max} \ge t_{i,J_i} + aps_{i,J_i} \quad \forall i
Cmax≥ti,Ji+apsi,Ji∀i
工序
O
i
j
O_{ij}
Oij的加工时间不仅取决于工序所选机器,还取决于其前序工序所属产品类型和加工完成时间
∑
k
p
k
i
j
⋅
v
i
j
k
=
p
s
i
j
∀
i
,
j
\sum_{k} p_{kij} \cdot v_{ijk} = ps_{ij} \quad \forall i,j
k∑pkij⋅vijk=psij∀i,j
a p s i j = { 0.75 p s i j p t i = p t h a n d x h g k l = 1 a n d x i j k l + 1 = 1 a n d T m e k l ≥ ∑ k c i , j − 1 , k p s i j e l s e aps_{ij}= \begin{cases} 0.75 ps_{ij}& pt_i = pt_h \ and \ x_{hgkl} = 1 \ and \ x_{ijkl+1}=1 \ and \ Tme_{kl} \ge \sum_k c_{i,j-1,k}\\ ps_{ij}& else \end{cases} apsij={0.75psijpsijpti=pth and xhgkl=1 and xijkl+1=1 and Tmekl≥∑kci,j−1,kelse
如果机器 k k k的当前最后一个工序的加工完成时间大于等于待加工工件工序的最早开始加工时间,并且当前加工工序与等待工序工件所属产品相同,则等待工序的加工时间缩短为75%。
同一工件的工序之间有先后关系
t
i
j
+
a
p
s
i
j
≤
t
i
,
j
+
1
∀
i
,
∀
j
=
1
,
.
.
.
,
J
i
−
1
t_{ij} + aps_{ij} \le t_{i,j+1} \quad \forall i,\forall j=1,...,J_i - 1
tij+apsij≤ti,j+1∀i,∀j=1,...,Ji−1
当前工序加工结束才能进行下一道工序加工
T
m
k
l
+
a
p
s
i
j
⋅
x
i
j
k
l
≤
T
m
s
k
,
l
+
1
∀
i
,
j
,
k
,
∀
l
=
1
,
.
.
.
,
d
k
−
1
Tm_{kl} + aps_{ij} \cdot x_{ijkl} \le Tms_{k,l+1} \quad \forall i,j,k,\forall l=1,...,d_k -1
Tmkl+apsij⋅xijkl≤Tmsk,l+1∀i,j,k,∀l=1,...,dk−1
T m s k l ≤ t i j + ( 1 − x i j k l ) ⋅ M ∀ i , j , k , l Tms_{kl} \le t_{ij} + (1-x_{ijkl}) \cdot M \quad \forall i,j,k,l Tmskl≤tij+(1−xijkl)⋅M∀i,j,k,l
T m s k l + ( 1 − x i j k l ) ⋅ M ≥ t i j ∀ i , j , k , l Tms_{kl} + (1-x_{ijkl})\cdot M \ge t_{ij} \quad \forall i,j,k,l Tmskl+(1−xijkl)⋅M≥tij∀i,j,k,l
工序与机器之间的选择关系
v
i
j
k
≤
a
k
i
j
∀
i
,
j
,
k
v_{ijk} \le a_{kij} \quad \forall i,j,k
vijk≤akij∀i,j,k
每个工件的工序都需要加工
∑
i
∑
j
x
i
j
k
l
=
1
∀
k
,
l
\sum_{i} \sum_{j} x_{ijkl} = 1 \quad \forall k,l
i∑j∑xijkl=1∀k,l
∑ k v i j k = 1 ∀ i , j \sum_{k} v_{ijk} = 1 \quad \forall i,j k∑vijk=1∀i,j
∑ l x i j k l = v i j k ∀ i , j , k \sum_{l} x_{ijkl} = v_{ijk} \quad \forall i,j,k l∑xijkl=vijk∀i,j,k
变量自身约束
t
i
j
≥
0
∀
i
,
j
t_{ij} \ge 0 \quad \forall i,j
tij≥0∀i,j
p s i j ≥ 0 ∀ i , j ps_{ij} \ge 0 \quad \forall i,j psij≥0∀i,j
T m s k l ≥ 0 ∀ k , l Tms_{kl} \ge 0 \quad \forall k,l Tmskl≥0∀k,l
T m e k l ≥ T m s k l ∀ k , l Tme_{kl} \ge Tms_{kl} \quad \forall k,l Tmekl≥Tmskl∀k,l
x i j k l ∈ { 0 , 1 } ∀ i , j , k , l x_{ijkl} \in \{0,1\} \quad \forall i,j,k,l xijkl∈{0,1}∀i,j,k,l
v i j k ∈ { 0 , 1 } ∀ i , j , k v_{ijk} \in \{0,1\} \quad \forall i,j,k vijk∈{0,1}∀i,j,k
1.5调度结果
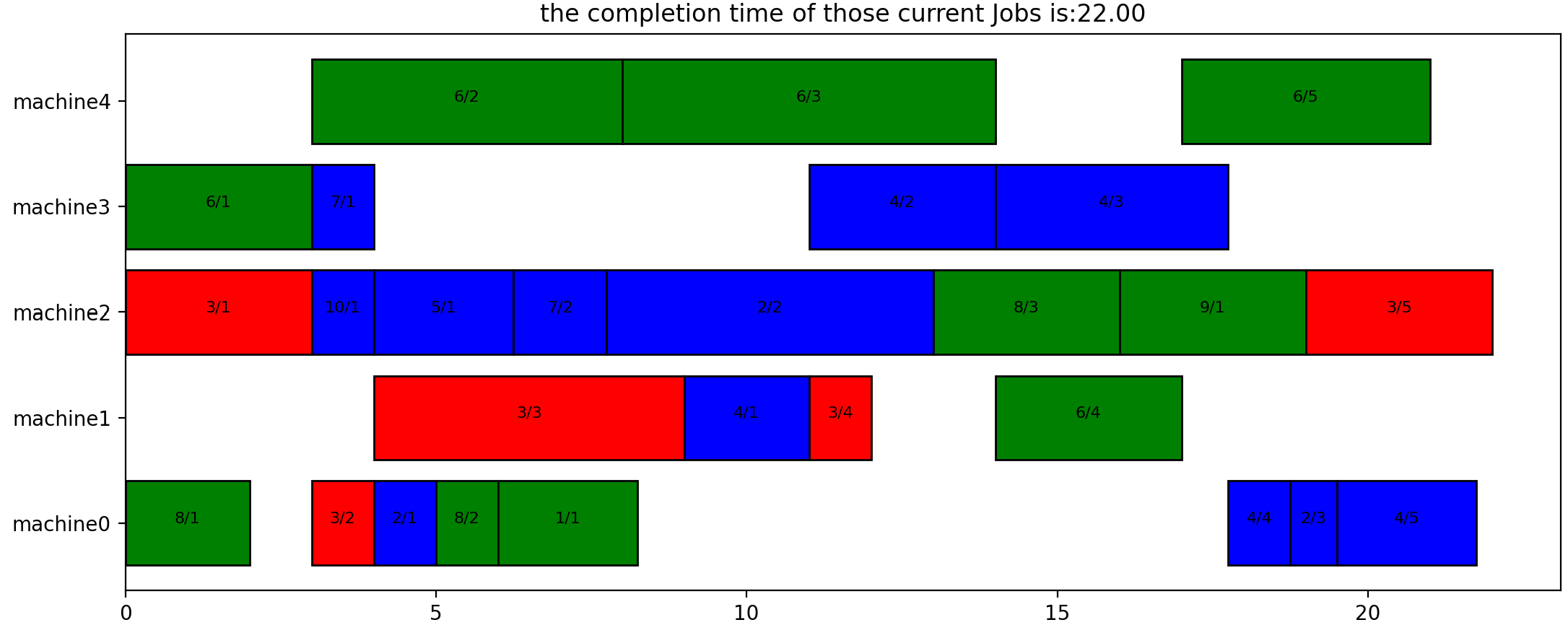
具体代码微信公众号【数学模型与算法】回复【FJSP】
[1]张国辉. 柔性作业车间调度方法研究[D].华中科技大学,2009.
[2] Demir Y , Isleyen S K . Evaluation of mathematical models for flexible job-shop scheduling problems[J]. Applied Mathematical Modelling, 2013, 37(3):977-988.

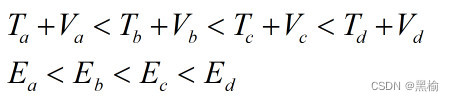

![[python bezier贝塞尔曲线] 数值解法、德卡斯特里奥解法解法以及bezier库的使用demo](https://img-blog.csdnimg.cn/30e4862eb7a94835a13d34b2d605181a.png)