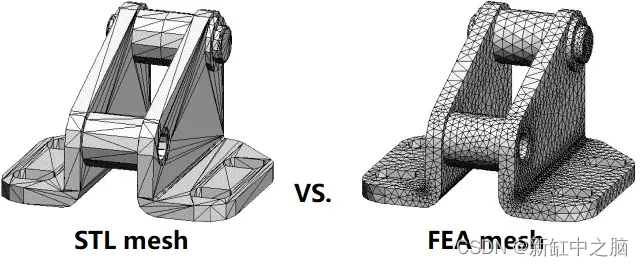
随着计算机图形学、硬件和3D打印技术的发展,基于曲面三角网格的图形渲染及其文件格式越来越流行。 在有限元分析(FEA)中,工程师有时会得到基于三角形网格的几何文件(如STL文件等)并进行后续分析。 由于曲面三角网格与有限元网格的根本区别,曲面网格不能直接用于有限元法的计算。 有必要将表面网格转换为 FEA 网格以进行后续分析。 本文概述了STL表面网格和有限元网格的特点,并举例说明了如何将STL网格转换为FEA网格。
推荐:用 NSDT设计器 快速搭建可编程3D场景。
1、三角面网格
三角网格是指由三角形单元组成的曲面模型。 它使用点和边形成许多小的空间三角形来近似 3D 模型的表面。 大多数基于 3D 网格的几何体也使用这种近似方法。 使用这种原始表示方法,几乎所有的 3D 模型表面都可以使用三角形来近似。 由于三角网格处理简单快捷、可视化好、性能好,被认为是描述三维模型的常用方法之一。 随着计算机图形学的飞速发展,三角网格模型在三维动画、电子商务、计算机辅助设计、制造、数字娱乐等诸多领域得到了广泛的应用。 特别是随着3D打印技术的蓬勃兴起,三角面网格成为3D模型表示方法的重点。 同时开发了不同的数据存储格式,其中应用广泛的有STL、OFF、OBJ、PLY等。

STL格式(Stereo Lithography的简称)是3D Systems于1988年开发的一种接口协议,是一种服务于快速原型制作技术的3D图形文件格式。 STL 文件由一系列无序的三角形面组成。 每个三角面的定义包括顶点坐标和三角面的法向量。 注意文件中没有给出三角形面之间的拓扑关系,三角形通过共享两个顶点相邻。 由于简单、不易出错,STL已经成为最常用的文件格式,成为快速成型技术领域事实上的接口标准。 目前市面上几乎所有的3D打印机都是通过识别STL模型进行打印。
另一种广泛使用的三角形格式是 OFF(对象文件格式)。 与STL文件不同的是,OFF文件给出了顶点的个数以及三角形和边的个数等信息,但OFF文件并没有指明三角形的法向量。 OFF文件可读性强,点集和面集简单明了。 它们都以 OFF 关键字开头,易于识别。 除了OFF文件,PLY(Standford triangle mesh)、OBJ等表面网格在工业界和学术界也有一些应用。 我们将在以后的文章中描述它们。
2、有限元分析中的 3D 网格
虽然在三维有限元分析中有一些特殊类型的单元,例如代表板(plate)和壳(shell)的面单元,代表桁架(truss)和梁(beam)的线单元。 但是,3D 实体元素使用最广泛。 常用的实体单元有四面体(terahedral)和六面体(hexahedral)单元,广泛应用于三维结构、热、流体、声学和电磁模拟。 实体单元不仅具有整体的表面信息,而且内部还有离散的网格。 这种差异也使得FEA实体网格比以STL为代表的面网格更加复杂,数据量也大得多。
有限元网格对单元的质量要求比较高。 元素不能过度扭曲。 网格密度需要适中。 粗网格会导致准确的问题。 而密集的网格会导致沉重的计算负担。 一些拓扑复杂的区域也需要密集网格。 常用的网格质量指标是:
- 雅可比比:由全局坐标和局部坐标得出的雅可比矩阵的比值。 理想值为 1,不能小于 0。
- 纵横比:指元素的最长边与最短边的比值。 理想元素的纵横比为 1。
- 偏度:元素规律性的量度。 取值范围为 0 到 1,值越小,元素越理想。
单元的排列顺序也会影响有限元分析的结果。 一般来说,二阶单元优于线性一阶单元,但二阶单元节点数的增加也会导致计算量相对较大。
3、将 STL 网格转换为 FEA 网格
通用有限元软件 WelSim 已经支持将 STL 曲面网格转换为实体网格以进行有限元分析。 用户可以通过导入STL文件快速完成网格划分项目,生成四面体实体网格(Tet4),导出FEA网格文件用于后续的有限元分析。
操作步骤如下:
1、在 WelSim 软件中,创建一个新的 FEM 项目,然后从菜单或工具栏中选择导入几何。 将弹出如下对话框:
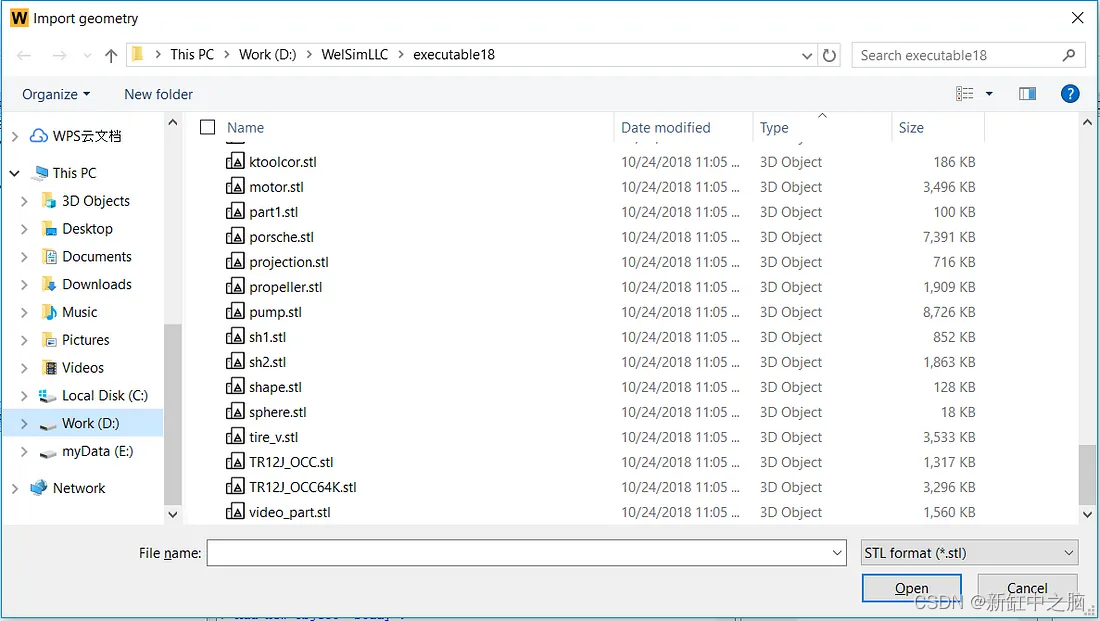
2、选择一个 STL 文件并单击“打开”。
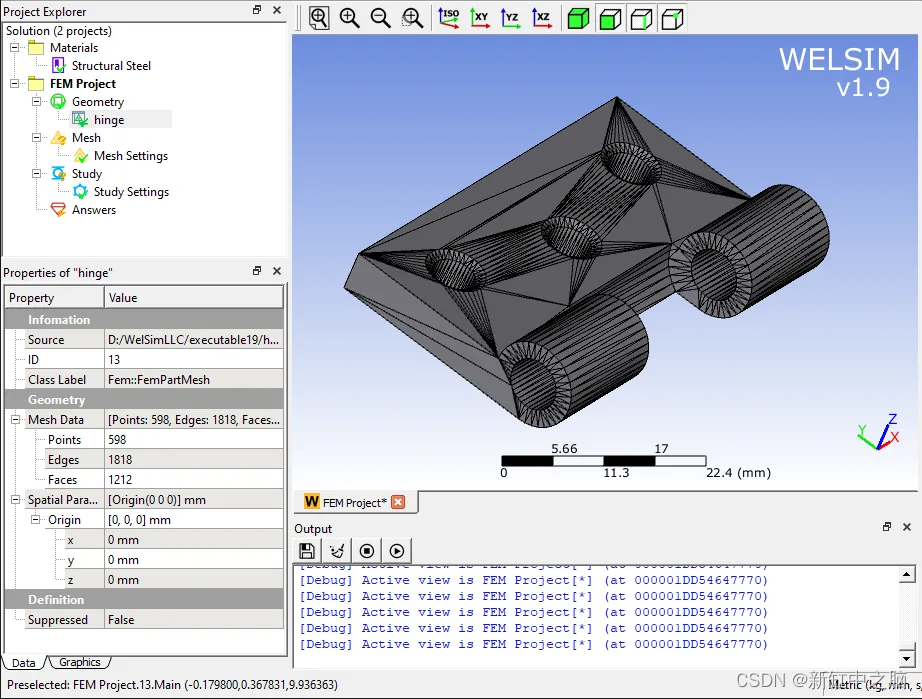
3、由于是STL几何模型,默认显示三角形网格线,用户可以在属性视图中选择隐藏网格线显示。
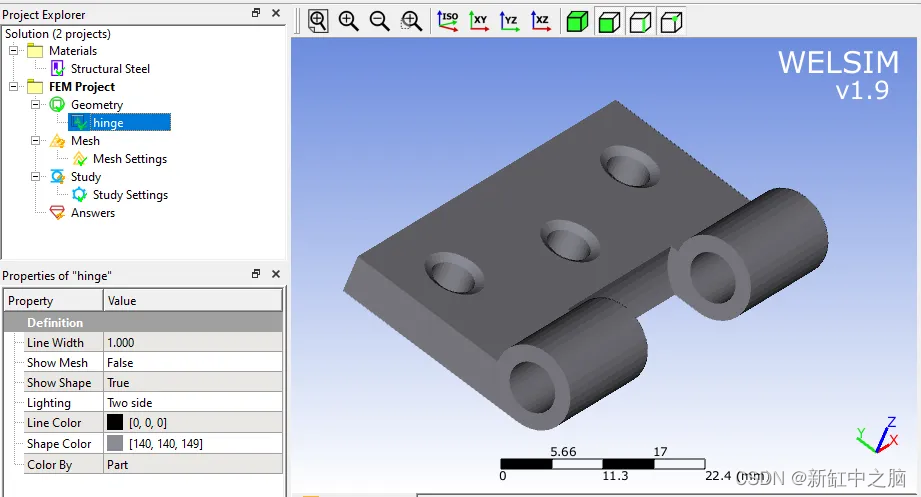
4、简单地设置元素的最大尺寸。 在这里,根据样本的整体尺寸,我们将最大单元尺寸设置为 10 mm。 单击 Mesh All 按钮执行有限元网格划分。
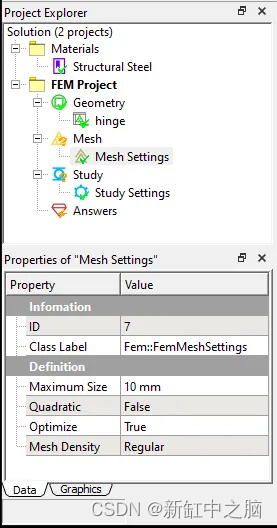
5、如下图,一共生成了4025个节点,16112个Tet4元素。
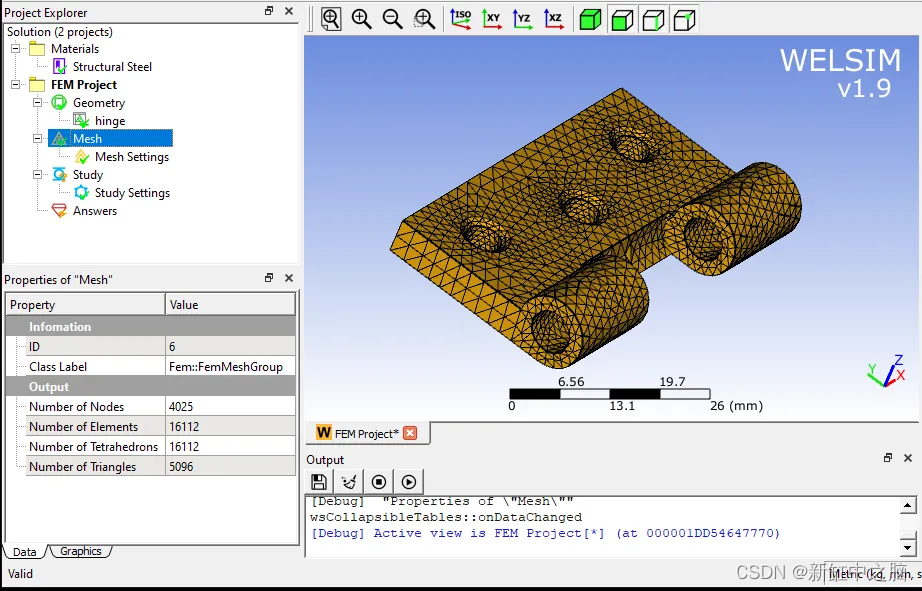
6、要将生成的有限元网格数据保存为文件,可以右键单击网格节点并选择导出网格。 如下所示:
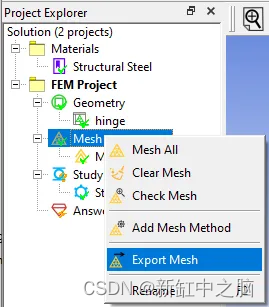
7、目前支持的网格文件格式有UNV,WelSim自带的格式,Abaqus的*.inp格式,Nastran的*.bdf格式,如下图。
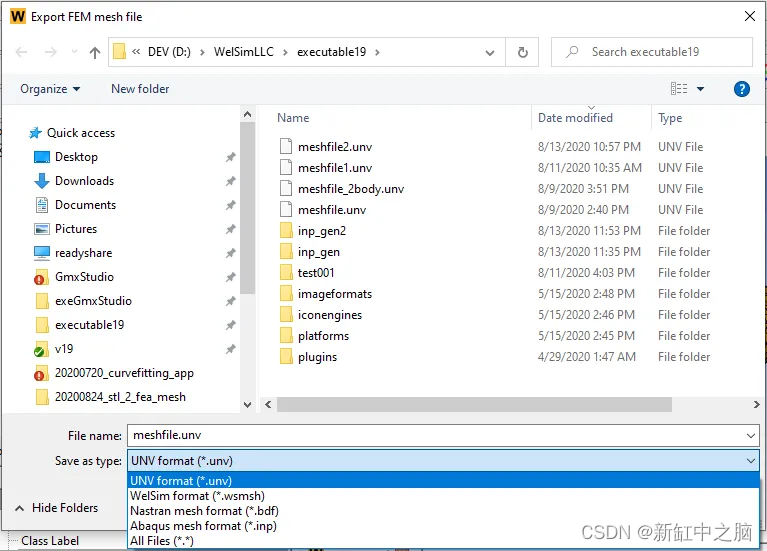
此时,STL 网格文件已转换为可用于有限元分析 (FEA) 或计算流体动力学 (CFD) 分析的实体网格。
原文链接:STL转有限元网格 — BimAnt