文章目录

前言
一. 整数除法
- 题目分析
- 1.一般思路
- - ①代码
- 2.优化思路
- - ②优化后的代码
- 拓展:用位运算实现整数的加法
- - ③代码
二. 二进制加法
- 题目分析
- 思路分析
- - ①代码
三. 前n个数字中1的个数
- 题目描述
- 思路分析
- - ①方法1——遍历
  - ②方法2——i&(i-1)
  - ③方法3——i&(i-1)的优化
  - ④方法4——奇偶分类
四. 只出现一次的数字
- 题目描述
- 一般思路
- - ①代码
- 进阶思路
- - ②代码
五. 单词长度的最大乘积
- 题目分析
- 一般思路
- - ①代码
- 进阶思路
- - ②代码
六. 排序数组中两个数字的和
- 题目分析
- 思路分析
- - 法①代码——双指针
  - 法②代码——二分查找
总结

前言

剑指offer专项突破版（力扣官网）——> 点击进入
本文所属专栏——>点击进入

一. 整数除法

题目分析

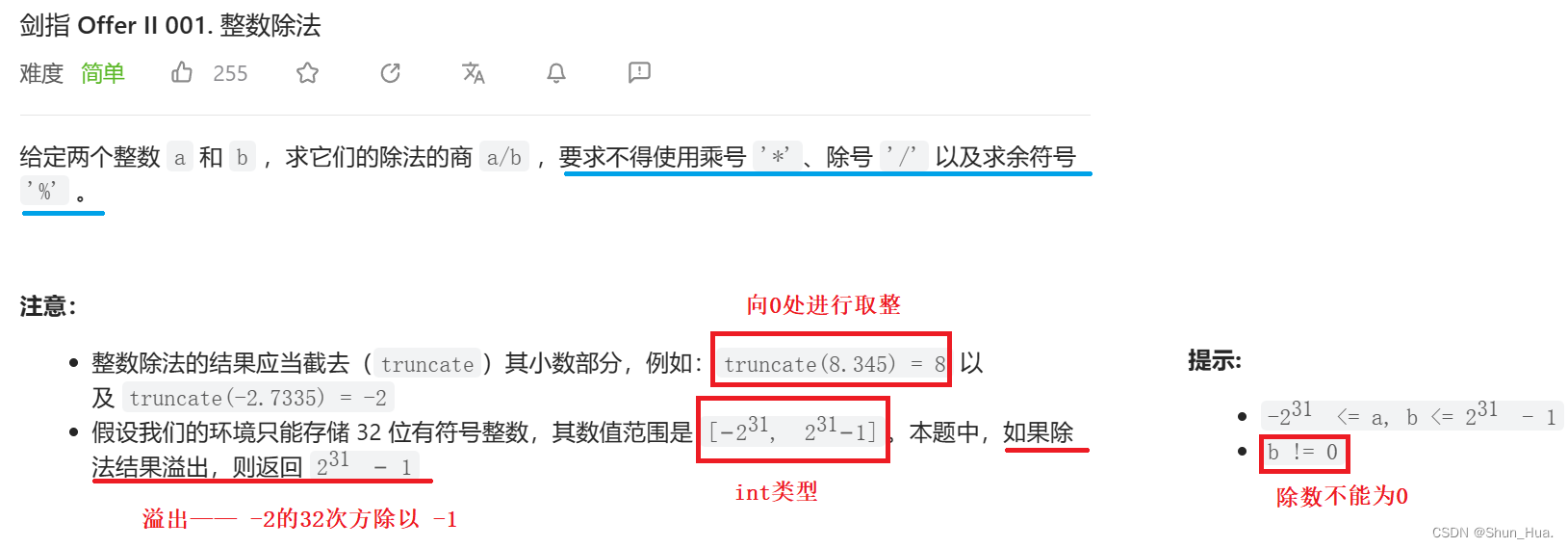
在这里插入图片描述

总结题目要求：

1.目的——实现除法
2.要求——不得使用 * / %
3.处理溢出—— -2³² / - 1 返回2³¹ - 1
4. 整数除法——向0取整，
说明：在其他语言中，比如Python的除法是相负无穷取整的—— -7 / 2 = - 3.5 向负无穷取整——结果为 - 4

1.一般思路

除法的商的意义是什么？——意义为除数的取多少倍才能等于被除数，或者取到多少倍再加1倍大于被除数。
转换为数学语言：设商为n，被除数为m，除数div，则 n * div = m 或者 (n*div<m并且(n+1)*div>m)。
当然不要忘了——这里成立的条件是除数大于等于0，被除数大于0
因此：可根据除数的多少倍——不断加上除数直到等于被除数或者刚好大于被除数即可，当刚好大于被除数时，我们只需对这个倍数减 1 即为商。
因此：我们只需不断的加上除数，并记录加的次数即可。
负数同理。
既然正负数都可以，那我们是选择将数都转换为负数还是正数进行计算呢？
这里就要考虑到边界问题——负数的边界是-2³² 正数的边界是2³¹ - 1。
如果这里选择正数那么必然会存在一个问题——如果除数或者被除数为 -2³²，转化为正数必然会溢出。
如果非要选处理这种情况，得不偿失，因此这里的最佳选择是都转换为负数。
如果那要转换我们要处理的第一个问题——符号，转换后商的正负性，无法进行保证，因此我们在处理前需要，确定商的正负性。
当然还有一个问题，这是一个不容易想到的问题，当在不断加除数时，会不会出现溢出的情况（有可能会出现），那如何判断呢？我想到了一个比较不错的方法——加了n倍的除数 + 除数 <= (int)0x80000000(负数)这是我们溢出的情况，那这个条件不是也和加了n倍的除数 <= (int)(0x80000000 - 除数) ，这样既判断了溢出情况，而且表达式也不会溢出！
除此之外加的次数可能会溢出也很难想到（-2147483648 /1这种情况）——所以我们设为负数即可，每次对
次数减一即可。最后对返回值再进行判断即可。

总结：

在转换前，确定商的符号，同号为正，异号为负。——a*b也可能溢出，因此只能单独判断。
将被除数和除数都转换为负数进行计算
判断溢出情况——加了n倍的除数 < (int)(0x80000000 - 除数)
说明——这个不成立就继续加，也就是加了n倍的除数 >= (int)(0x80000000 - 除数)成立，可继续加除数。

①代码

int divide(int a, int b)
{
    //对特殊情况进行判断
    if(a==0x80000000 && b==-1)
    {
        return 0x7FFFFFFF;
    }
    //判断商的符号
    //当被除数为0时，直接返回0即可
    if(a == 0)
    {
        return 0;
    }
    //假设为正
    int signal = 1;
    //判断为负数的情况
    if((a>0&&b<0)||(a<0&&b>0))
    {
        signal = -signal;
    }
    //都转换为负数
    if(a>0)
    {
        a = -a;
    }
    if(b>0)
    {
        b = -b;
    }
    //运算得商
    int count = 0;
    int cur = 0;
    //说明：这里的0x80000000是无符号整形，表达会整形提升为unsigned。
    //因此需将结果转换为int类型。
    while((cur>=(int)(0x80000000-b))&&a<cur)
    {
        cur+=b;
        count--;
    }
    if(cur<a)
    {
        count++;
    }
     return signal == -1?count:-count;
}

可惜思路对了，但是超出时间限制了。
原因——测试用例 -2147483648 和 1 会计算21亿多次，这样力扣的编译器是不会给我们过的。

2.优化思路

前面的大致思路都是没问题的，但就是太慢了。
如何快一点呢？

慢的关键在于每次只加了一次除数。
因此我们每次多加几次就行了，那怎样多加呢？

举例：-15 和 -2

设置每次加本身的初始值为除数，那么倍数n就为1

n	每次加本身后的值	n的规律
1	-2 —— -2*1	初始值——1
2	-4 —— -2*2	1+1= 2
4	-8—— -2*4	2+2 = 4
8	-16 —— -2*8	4+4= 8

这样每次进行相加，都相当于乘2，这是一个很快的速度。

那我们如何求商呢？

如果这样算每次加本身的值有三种情况：——我们这里考虑的是负数的情况，所以符号别弄反了！
1.小于——没法进行计算
2.大于——可以用被除数减去此值，然后问题转换为新的被除数与原来除数的商是多少。
3.等于——直接出结果即可
那如何让加本身的结果（设为n）小于等于被除数呢？
那就让n+n >被除数时进入循环即可

总结

前提: n+n >被除数时进入循环,并且n+n不能溢出——n >= (int)(0x80000000 - n )
1.大于被除数时，用被除数减去此值，然后问题转换为新的被除数与原来除数的商是多少（继续循环，直到被除数大于除数）。
2.等于直接输出即可。

模拟运算 : -15(被除数) 和 -2(除数)

-8±8小于-16，因此跳出循环，此时为倍数为4，加到总倍数上去，将被除数更新为15-（-8）= -7<-2
-4 + -4 小于-7 ,因此跳出循环，此时为倍数为2，加到总倍数上去，将被除数更新为-7-（-4）= -3<-2
-2±2 小于-4 ,因此跳出循环，此时为倍数为1，加到总倍数上去，将被除数更新为-3-（-2）= -1>-2,跳出循环。
因此总倍数——4+2+1 = 7

②优化后的代码

int divide(int a, int b)
{
    //对特殊情况进行判断
    if(a==0x80000000 && b==-1)
    {
        return 0x7FFFFFFF;
    }
    //判断商的符号
    //当被除数为0时，直接返回0即可
    if(a == 0)
    {
        return 0;
    }
    //假设为正
    int signal = 1;
    //判断为负数的情况
    if((a>0&&b<0)||(a<0&&b>0))
    {
        signal = -signal;
    }
    //都转换为负数
    if(a>0)
    {
        a = -a;
    }
    if(b>0)
    {
        b = -b;
    }
    //运算得商

    //说明：这里的0x80000000是无符号整形，表达会整形提升为unsigned。
    //因此需将结果转换为int类型。
    int sum_count = 0;
    while(a<=b)
    {
        int count = -1;//是为了处理-2147483648 1这种情况
        int cur = b;
        while((cur>=(int)(0x80000000-cur))&&a<=cur+cur)
        {
            cur+=cur;
            count+=count;
        }
        //更新被除数
        a = a-cur;
        //加上总倍数
        sum_count+=count;
    }
    return signal == -1 ? sum_count : -sum_count;
}

拓展:用位运算实现整数的加法

③代码

#include<stdio.h>
int main()
{
	int begin = 0;
	int process = 0;
	int end = 0;
	scanf("%d%d", &begin, &end);
	process = end;//为了进入第一次的循环
	while (process)//当没有进位信息，就停止循环
	{
		//先进行异或不保留进位信息
		end = begin ^ process;
		//获取进位信息，左移之后是进位
		process = (begin & process) << 1;
		//更新下一轮的加数信息
		begin = end;
	}
	printf("%d\n", end);
	return 0;
}

二. 二进制加法

题目分析

在这里插入图片描述

总结题目信息：

要求——将字符串相加，并将结果用字符串进行输出。
数据格式：字符串非空，只含01序列，不含001这样的字符串。字符串存储的最大数据为2¹⁰⁰⁰¹ -1

思路分析

因为字符串中存储的数据很大，因此不能转换为整数进行计算。
我们可以取出字符串的每一位（从个位开始）进行相加，当然还要考虑进位信息（个位不用，因此设置为0）。

指定位的信息	指定位的信息	进位信息	加结果
1	1	0	0
1	1	1	1
1	0	1	0
1	0	1	0

剩下的这里就不列了
结论：这里相当于加法的结果相当于将指定位的信息与进位信息进行异或。

那进位信息如何表示呢？

分为三种情况:
1.指定位的信息都为1 。也就是 1 1 ——进位为1
2.指定位的信息都为0。不管上一位的进位都是0
3.指定位的信息有一个1，1 0和0 1这种情况，如果上一位的进位是1，那么进位为1 ，如果为0 进位为0。
如何表示：
设第一个字符串的指定位的信息为 n1，第二个字符串的指定位置的信息为n2.
则进位carry = (n1&n1)|((n1|n2)&carry),右边表达式的carry是上一次的进位信息。
说明：n1&n2是第一种情况（n1|n2）& carry是第三种情况。

关键的思路说完了，剩下的是一些细节：

1.如何将字符串的每一位取出，转换为正数。

从末尾依次开始取，然后减去字符0，即可得到指定位的信息。

2 .要开辟多大的空间。

因为最高位可能会有进位信息，最后一个位置还要存\0,因此我们要开辟的是最大字符串长度加2。

3 .最后可能会有进位信息，因此最后也要判断一下。
4 .最后的字符串是倒着的，因此我们需要把最后求得的字符串再逆转一下。

思路总结：

1.求所要开辟字符串的最大空间——最大字符串的长度加2。
2.将字符串的每一位取出倒着取出来，依次进行异或获取当前位的结果，进行按位与与按位或运算得到进位信息。
3. 判断最后是否还有进位信息。
4. 逆转字符串——有进位信息和无进位信息的最后下标是不同的。

①代码

void reverse(char* string ,int right)
{
    int left = 0;
    while(left<=right)
    {
        char tmp = string[left];
        string[left] = string[right];
        string[right] = tmp;
        left++;
        right--;
    }
}
char * addBinary(char * a, char * b)
{
    //开辟指定目标字符串的空间
    int len_a =strlen(a);
    int len_b =strlen(b);
    int size = len_a > len_b ? len_a + 2: len_b + 2;
    char* string = (char*)malloc(sizeof(char)*size);
    //初始化字符串
    memset(string,0,sizeof(char)*size);
    int end = -1;//最后一个位置的下标
    //求进位信息
    char* string_a =a;
    char* string_b =b;
    //表示最后一位的下标
    len_a--;
    len_b--;
    //进位信息
    int carry = 0;
    
    while(len_a>=0||len_b>=0)
    {
        //获取指定位的信息
        //可能有len_a和len_b为负的情况
        int add_a = len_a>=0?a[len_a] - '0':0;
        int add_b = len_b>=0?b[len_b] - '0':0;
        //结果位的信息
        int cur = add_a^add_b^carry;
        //进位信息
        carry = (add_a&add_b)|((add_a|add_b)&carry);
        //将结果位加到指定字符串
        string[++end] = cur+'0';
        //printf("%c",string[end]);
        //调整len_a和len_b
        len_a--;
        len_b--;
    }
    //最后一次是否有进位
    if(carry==1)
    {
        string[++end]='1';
    }
    //逆转字符串
    reverse(string,end);
    return string;
}

三. 前n个数字中1的个数

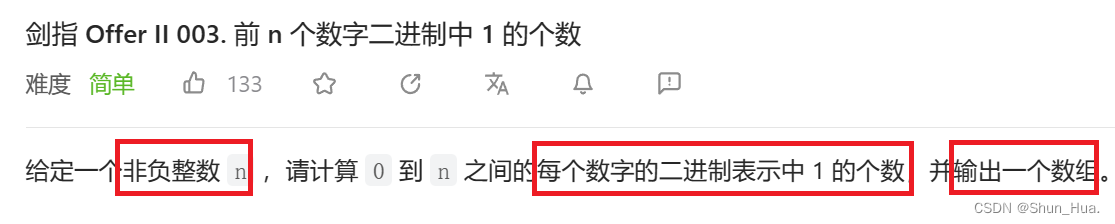
在这里插入图片描述

题目描述

要求：求0-n的二进制中1的个数，输出一个数组。
数据格式：非负整数。

思路分析

求0到n之间的数，因此要开辟的数组大小为 n+1
求数字的二进制中1的个数。

思路1：让数字的每一位依次与1按位与，结果为1，说明指定位是1，反之是0.

思路2：设整数为i，则i&(i-1),相当于把i的最右边的1消去，也就是说不断进行
i&(i-1)会将i的二进制1的个数消完，于是我们可以利用i作为循环条件，每次进行此操作，再将结果赋值给i，进行多少次循环，意为有多少个1.

思路3: 利用思路二，i比i&(i-1)的二进制位多一个，且i大于i&(i-1),因此我们可以利用这个关系进行求解,前提是得有一个已知的值。
函数表达式 ——arr[ i ] = arr[ i & (i-1) ] + 1;

思路4:
1.奇数比它前面的一个数多一个1，比如3比2多一个1。
2.偶数跟它的2倍有相同的1，比如10跟5的1的个数是一样的。因为乘2即为左移1。
于是我们可以这样表达：
arr[i] = arr[i/2] ;——i是偶数
arr[i] = arr[i-1] + 1 = arr[(i-1)/2] +1 = arr[i>>1] + 1;——i是奇数
合并一下即为——arr[i] = arr[ i>>1] + i &1 。 i&1判断i是否为奇数

思路总结：

1.开辟n+1个整形的空间
2.按照三种思路进行求解。

①方法1——遍历

int* countBits(int n, int* returnSize)
{
    //开辟数组
    int *arr =(int*)malloc(sizeof(arr)*(n+1));
    *returnSize = n + 1;
    memset(arr,0,sizeof(arr)*(*returnSize));
    //遍历求解
    for(int i = 0;i < n+1; i++)
    {
        int count = 0;
        //每一位都要按位与1
        for(int j = 0; j < 32; j++)
        {
            if(((i>>j)&1)==1)
            {
                count++;
            }
        }
        arr[i] = count;
    }
    return arr;
}

②方法2——i&(i-1)

int* countBits(int n, int* returnSize)
{
    //开辟数组
    int *arr =(int*)malloc(sizeof(arr)*(n+1));
    *returnSize = n + 1;
    memset(arr,0,sizeof(arr)*(*returnSize));
    for(int i = 0;i < n+1; i++)
    {
        int tmp_i = i;
        int count = 0;
        while(tmp_i)
        {
            count++;
            tmp_i&=(tmp_i-1);
        }
        arr[i] = count;
    }
    return arr;
}

③方法3——i&(i-1)的优化

int* countBits(int n, int* returnSize)
{
    //开辟数组
    int *arr =(int*)malloc(sizeof(arr)*(n+1));
    *returnSize = n + 1;
    memset(arr,0,sizeof(arr)*(*returnSize));
	for(int i = 1;i<n+1;i++)
    {
        arr[i] = arr[i&(i-1)] + 1;
    }
    return arr;
}

④方法4——奇偶分类

int* countBits(int n, int* returnSize)
{
    //开辟数组
    int *arr =(int*)malloc(sizeof(arr)*(n+1));
    *returnSize = n + 1;
    memset(arr,0,sizeof(arr)*(*returnSize));
    //运算思路
    for(int i = 0; i < n+1;i++)
    {
        arr[i] = arr[i>>1] + (i&1); 
        //说明：位运算的优先级很低，所以这里i&1必须加括号！
    }
    return arr;
}

四. 只出现一次的数字

题目描述

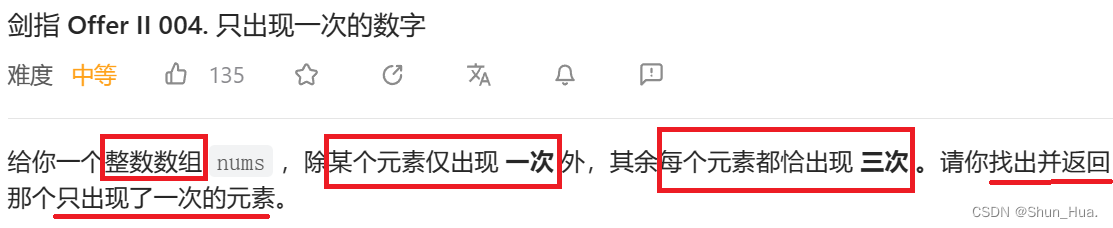
在这里插入图片描述

要求：找到并返回只出现一次的元素
条件: 每个元素恰出现三次，并且数组是int类型的。

一般思路

1.直接找到只出现一次的元素即可。
因此：我们可以暴力求解，两层for循环。

①代码

int singleNumber(int* nums, int numsSize)
{
    int only = 0;
    for( int i = 0; i < numsSize; i++)
    {
        int is_repeat = 0;//假设当前元素没有重复的
        for(int j = 0; j < numsSize; j++)
        {
            if(i!=j)
            {
                if(nums[i]==nums[j])
                {
                    is_repeat = 1;//如果有重复的就无需再进行判断。
                    break;
                }
            }
        }
        if(is_repeat==0)
        {
            only = nums[i];//如果没有重复的,说明找到了。
            break;
        }
    }
    return only;
}

这种方法虽然能过力扣的编译器，但是还是比较慢的。

进阶思路

1.既然相同的数出现了3次，那么指定二进制位相加的结果再模上三，就必然为0。举个例子—— 7 7 7，这三个的二进制都是111，那三个二进制位分开相加，结果就是 3 3 3 出现3次，因此模3等于0。
2 .那把所有的数的位数相加，再模上3就把出现三次的就都消去了，剩下的就是，出现一次的位数（模三等于0那便是0，不等于0那便是1）。这样出现一次的数的二进制位就都有了，我们再进行移位操作，即可得到只出现一次的值。

举例: 3, 3, 3, 1

十进制表示	二进制表示	第一位(从左向右)	第二位
3	11	1	1
3	11	1	1
3	11	1	1
1	1	0	1
		相加结果	相加结果
		3	4
		模3	模3
		0	1
		转换为十进制	01—— >1

因此只出现一次的元素是1。

思路总结

开一个数组——32个整形——存储每一位的信息
将每一二进制位的信息，加到数组当中。
数组每一位%3获取只出现一次的数的二进制位的表达形式。
将二进制位再转换为十进制进行输出。

②代码

int singleNumber(int* nums, int numsSize)
{
    //开辟并初始化空间
    int *arr =(int*)malloc(sizeof(int)*32);
    memset(arr,0,sizeof(int)*32);
    //获取每一位的位数
    for(int i = 0; i < numsSize; i++)
    {
        for(int j = 0; j < 32; j++)
        {
            if(((nums[i]>>j)&1)==1)
            {
                arr[31-j] +=1;
            }
        }
    }
    //将每一位模3获取只出现1次的数字的二进制位

    for(int i = 0; i < 32; i++)
    {
        arr[i] = arr[i] % 3;
    }
    //将二进制位转换为十进制
    int ret = 0;
    for(int i = 0; i < 32; i++)
    {
        ret = (((unsigned int)ret<<1) | arr[i]);
    }

    //记得释放空间
    free(arr);
    arr = NULL;
    return ret;
}

五. 单词长度的最大乘积

题目分析

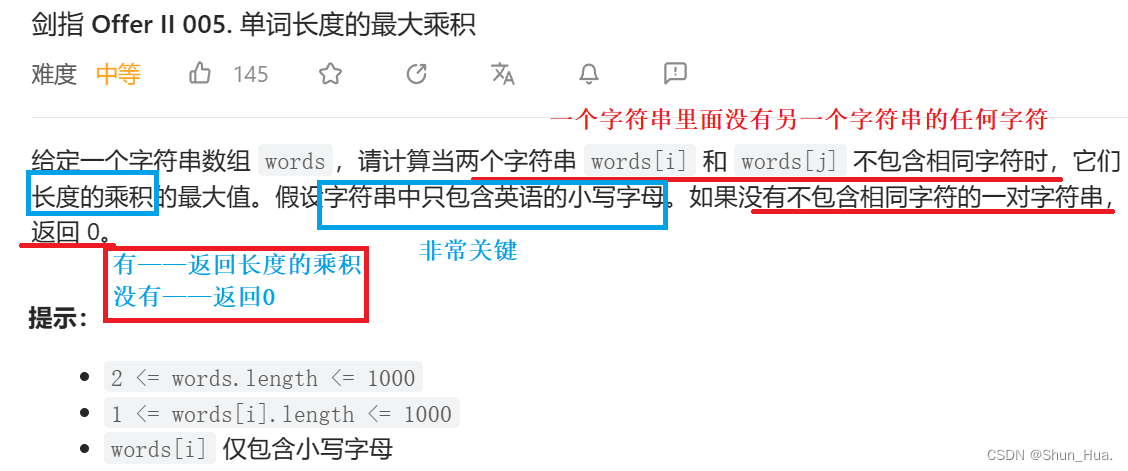
在这里插入图片描述

总结

1 .数据格式——字符串中只包含小写字母
2 .题目要求——返回不相等字符串的乘积
3 . 返回格式——有不同字符串最大长度乘积，无返回0

一般思路

1 .找到不同字符串，计算长度乘积。
2 .跟当前最长的乘积相比，如果比它大就更新。

①代码

bool is_dif_str(char* str1,char* str2)
{
    while(*str1!='\0')
    {
        char *tmp = str2;
        while(*tmp!='\0')
        {
            if(*str1==*tmp)
            {
                return false;
            }
            else
            {
                tmp++;
            }
        }
        str1++;
    }

    return true;
}

int maxProduct(char ** words, int wordsSize)
{
    int  max_product = 0;
    for(int i = 0; i < wordsSize; i++)
    {
        for(int j = i+1; j < wordsSize; j++)
        {
            if(is_dif_str(words[i],words[j]))//判断字符串不同
            {
                int len_i = strlen(words[i]);
                int len_j = strlen(words[j]);
                int product = len_i * len_j;
                if(max_product<product)
                {
                    max_product = product;
                }
            }
        }
    }
    return max_product;
}

这种暴力求解的复杂度量级接近于n的4次方（只是估算），可以看出时间复杂之高，因此过不了力扣的编译器很正常。

进阶思路

1 . 既然字符串的格式是只有小写字符—— 一共26个，那一个字符串的字符的可能性只有26种，这26种可能性用int类型的32位存，也刚好。那要怎么存呢？从右向左，依次存储a到z即可，怎么存呢？按位或上1左移字符减去字符a的结果即可。表达式：|=(1<<(字符-‘a’))

2 . 既然可以转换成二进制的的形式，那怎么判断两个字符串是否不同呢？答案很简单——按位或，按位或当字符串的结果都不同时，结果为0，如果相同，结果就不为0。
3 . 字符串转换的整形进行按位与，遍历即可。

思路总结

1 .开辟一个与存储字符串数组相同个数的整形数组。
2 .将字符串的信息转换为整形，存到整形数组。
3 . 对整形数组用与运算进行遍历。

②代码

int maxProduct(char ** words, int wordsSize)
{
    //开辟并初始化空间
    int *arr =(int *)malloc(sizeof(int)*wordsSize);
    memset(arr,0,sizeof(int)*wordsSize);
    //将字符串转换为二进制信息
    for(int i = 0; i < wordsSize; i++)
    {
        char* cur = words[i];
        while(*cur!='\0')
        {
            arr[i] |= (1<<(*cur-'a'));
            cur++;
        }
    }
    //循环遍历
    int max_product = 0;
    for(int i = 0; i < wordsSize; i++)
    {
        for(int j = i+1; j < wordsSize; j++)
        {
            if((arr[i]&arr[j])==0)
            {
                int len_i = strlen(words[i]);
                int len_j = strlen(words[j]);
                int product = len_i*len_j;
                if(product>max_product)
                {
                    max_product = product;
                }
            }
        }
    }
    //释放空间
    free(arr);
    arr = NULL;
    return max_product;
}

六. 排序数组中两个数字的和

题目分析

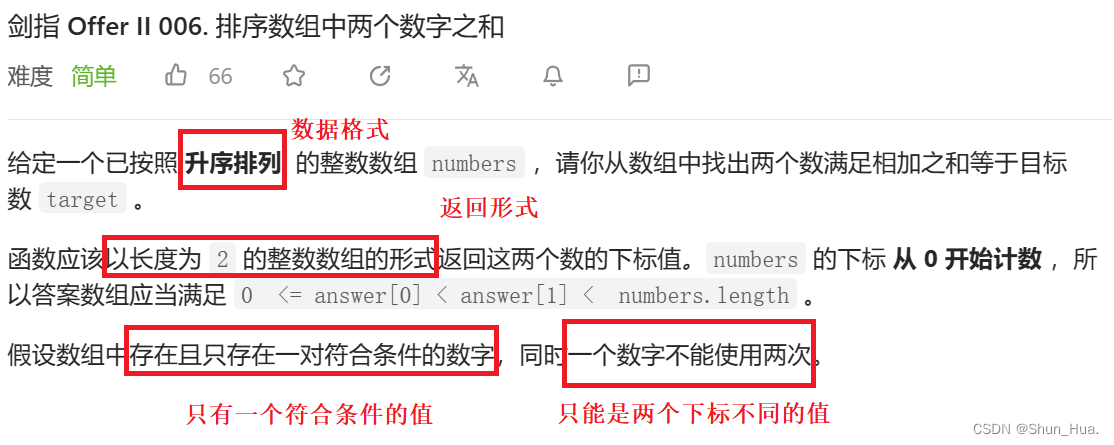
在这里插入图片描述

思路分析

关键：利用好升序数组的特性
思路1：可以利用双指针，一个左下边标，一个右下标，这样比目标数大，就让右下标右移，调小。比目标数小，就让左下标左移，调大。
思路2：固定一个值（可以从左边也可以从右边），那么要找的数就是目标值-这个固定的值，这个固定的值就可以利用二分法进行查找。

法①代码——双指针

int* twoSum(int* numbers, int numbersSize, int target, int* returnSize)
{
    //开辟空间并初始化数组
    int *arr = (int*)malloc(sizeof(int)*2);
    *returnSize = 2;
    memset(arr,0,sizeof(int)*2);
    //双指针查找思路
    int left = 0;
    int right = numbersSize - 1;
    while(left < right)
    {
        int sum = numbers[left]+numbers[right];
        if(sum > target)
        {
            right--;
        }
        else if(sum < target)
        {
            left++;
        }
        else
        {
            arr[0] = left;
            arr[1] = right;
            break;
        }
    }
    
    return arr;
}

法②代码——二分查找

int* twoSum(int* numbers, int numbersSize, int target, int* returnSize)
{
    //开辟空间并初始化数组
    int *arr = (int*)malloc(sizeof(int)*2);
    *returnSize = 2;
    memset(arr,0,sizeof(int)*2);
	//二分查找思路
    for(int i = 0; i < numbersSize; i++)
    {
        //从左边开始
        int left = i+1;
        int right = numbersSize - 1;
        int mid = (left+right)/2;
        int Target = target - numbers[i];
        int flag = 0;
        while(left<=right)//这里是可以相等的，因为我要找的是一个数
        {
            if(numbers[mid]>Target)
            {
                right = mid - 1;
            }
            else if(numbers[mid]<Target)
            {
                left = mid + 1;
            }
            else
            {
                flag = 1;
                break;
            }
            //更新mid
            mid = (left+right)/2;
        }
        if(flag)
        {
            arr[0] = i;
            arr[1] = mid;
            break;
        }
    }
    
    return arr;
}

总结

1. 在整数除法中我们必须处理好边界情况。
1. 在二进制加法中我们需要处理好最后一次的进位信息，以及如何正确表示进位。
1. 前n个数字中1的个数，方法4的位运算的优先级很低，因此一旦涉及位运算就要加括号。
1. 对于某个数字出现m次，某个数字出现n次，m!=n这类题，我总结为两种情况，第一种情况：如果m为偶数， n为奇数。直接异或得结果；第二种情况，我们还是将每一位加起来，再模m，如果结果为0 那一位就为0，如果结果不为0，那一位就为1。
1. 单词的长度乘积这道题，关键点在于都是小写字母我们才可以用int表示，如果不是我们可能需要用更大的进行表示。
1. 排序数组中两个数字的和，这道题关键在于利用好升序的条件，二分或者双指针均可。