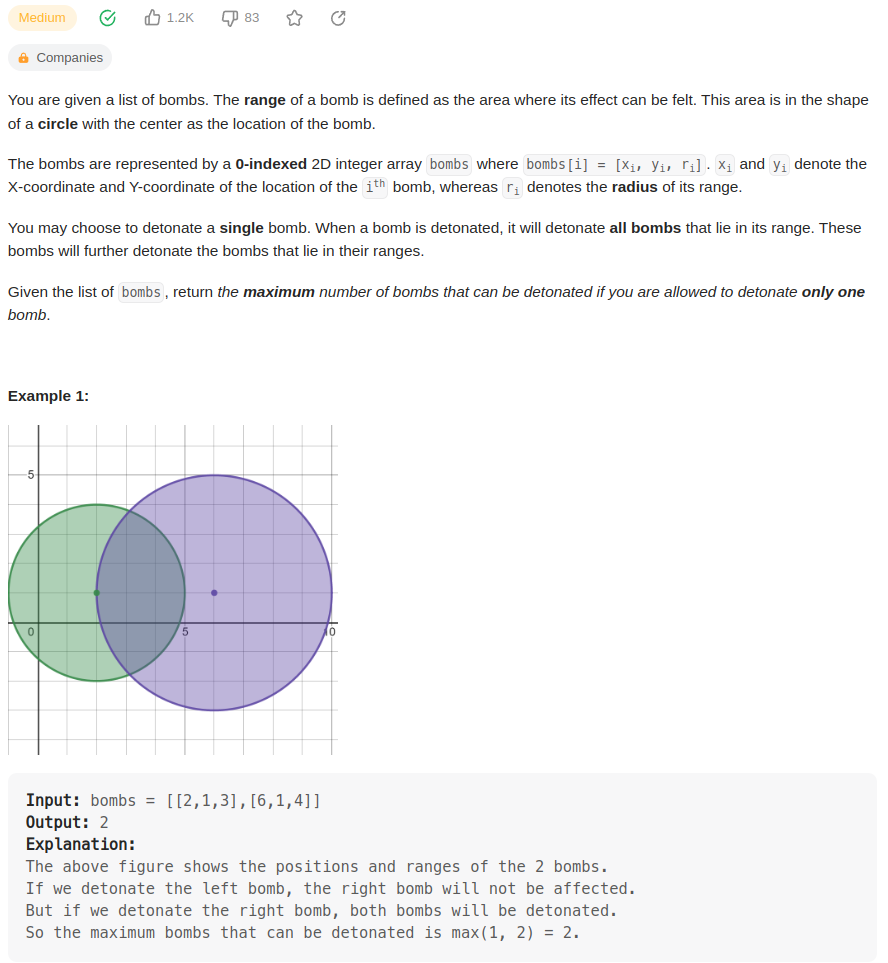
bombs是一个二维数组，每个bombs[i] = [x, y, r] 代表一个bomb，(x,y)是二维坐标，r是半径。
点燃一个bomb时，以(x,y)为圆心，半径为r的圆范围内的bomb都会点燃，引起连锁反映。
选择一个bomb点燃，使得最后能点燃的bomb数最多。

思路：

因为点燃bomb时是连锁反应，1点燃2，2又点燃3，
所以是一个DFS的思想。

而只能点燃一个bomb，那么就是在1 ～ n的bomb中，找到第 ℹ 个，使 dfs (bombs, i ) 最大。

dfs中需要一个visited数组，记录是否已经访问过。

一次只能点燃一个bomb，所以最初点燃的每个dfs(bombs, i) 是一个全新的过程，visited数组要重置，
点燃的bomb数cnt 置0.

在dfs内部：
只有两个bomb之间的距离 <= 当前bomb的半径，才会点燃下一个，进入下一个dfs.
每进入一个dfs, 就表示点燃了那个bomb，cnt++.
在一个dfs过程中，点燃完之后visited不用置false, 因为bomb只能点一个，点了就没有了。

举个例子，
假设1能点燃2，3， 而且2，3都能点燃4，且距离都在半径范围内。

那么dfs(1)后进入dfs(2), dfs(2)中进入dfs(4), 每次dfs内都是cnt++, 这一轮结束后cnt=3,
这时visited[1,2,4] = true
然后在dfs(1)内部进入dfs(3), dfs(3)内部发现visited[4]已经为true, 不再点燃4，只点燃3本身，
这一轮在dfs(3)处cnt++.
虽然3没有点燃4，但是4已经被2点燃，由1点燃的2,3,4bomb总数是一致的。
所以dfs(1) 最终的cnt=4.

然后开始新的一轮dfs(2). dfs(3), dfs(4)

做一个剪枝，当某一个dfs结果为n（bomb总数）时，不需要再计算，因为没有更多了。

另外，x, y, r最大为10⁵, 这就意味着在求平方时会超过整数范围，所以用long型。

class Solution {   
    int n;
    int count = 0;
    public int maximumDetonation(int[][] bombs) {
        n = bombs.length;
        int res = 0;

        for(int i = 0; i < n; i++) {           
            count = 0;
            
            dfs(bombs,i, new boolean[n]);       
            res = Math.max(res, count);
            if(res == n) return res;
        }
        return res;
    }

    void dfs(int[][] bombs, int idx, boolean[] visited) {       
        count ++;
        visited[idx] = true;
        
        for(int i = 0; i < n; i++) {
            if(visited[i]) continue;
            
            long dx = bombs[i][0] - bombs[idx][0];
            long dy = bombs[i][1] - bombs[idx][1];
            long r = bombs[idx][2];
            
            if(dx*dx + dy*dy <= r*r) dfs(bombs, i, visited);
        }     
    }  
}