0. 引言

深度学习模型架构越复杂越好吗？

自过去的几十年里，人工神经网络取得了显著的进展，这归功于一种理念：增加网络的复杂度可以提高性能。从 AlexNet 引爆了深度学习在计算机视觉的热潮后，研究者们为了提升深度网络的性能，精心地设计出了各种各样的模块，包括 ResNet 中的残差，ViT 中的注意力机制等。然而，尽管深层的复杂神经网络可以取得很好的性能，但他们在实际应用中的推理速度往往会受到这些复杂操作的影响而变慢。

来自华为诺亚、悉尼大学的研究者们提出了一种极简的神经网络模型 VanillaNet，以极简主义的设计为理念，网络中仅仅包含最简单的卷积计算，去掉了残差和注意力模块，在计算机视觉中的各种任务上都取得了不俗的效果。13 层的 VanillaNet 模型在 ImageNet 上就可以达到 83% 的精度，挑战了深度学习模型中复杂设计的必要性。

论文名称：VanillaNet: the Power of Minimalism in Deep Learning
论文地址：https://arxiv.org/abs/2305.12972
代码地址：https://github.com/huawei-noah/VanillaNet 或
                 https://gitee.com/mindspore/models/tree/master/research/cv/vanillanet

1. 网络结构

VanillaNet6的网络结构如下所示。从图中可以看出，整个VanillaNet6网络结构极其简单，由 5 个卷积层，5 个池化层，一个全连接层和 5 个激活函数构成，结构的设计遵循 AlexNet 和 VGG 等传统深度网络的常用方案：分辨率逐渐缩小，而通道数逐渐增大，不包含shortcut，attention等计算。

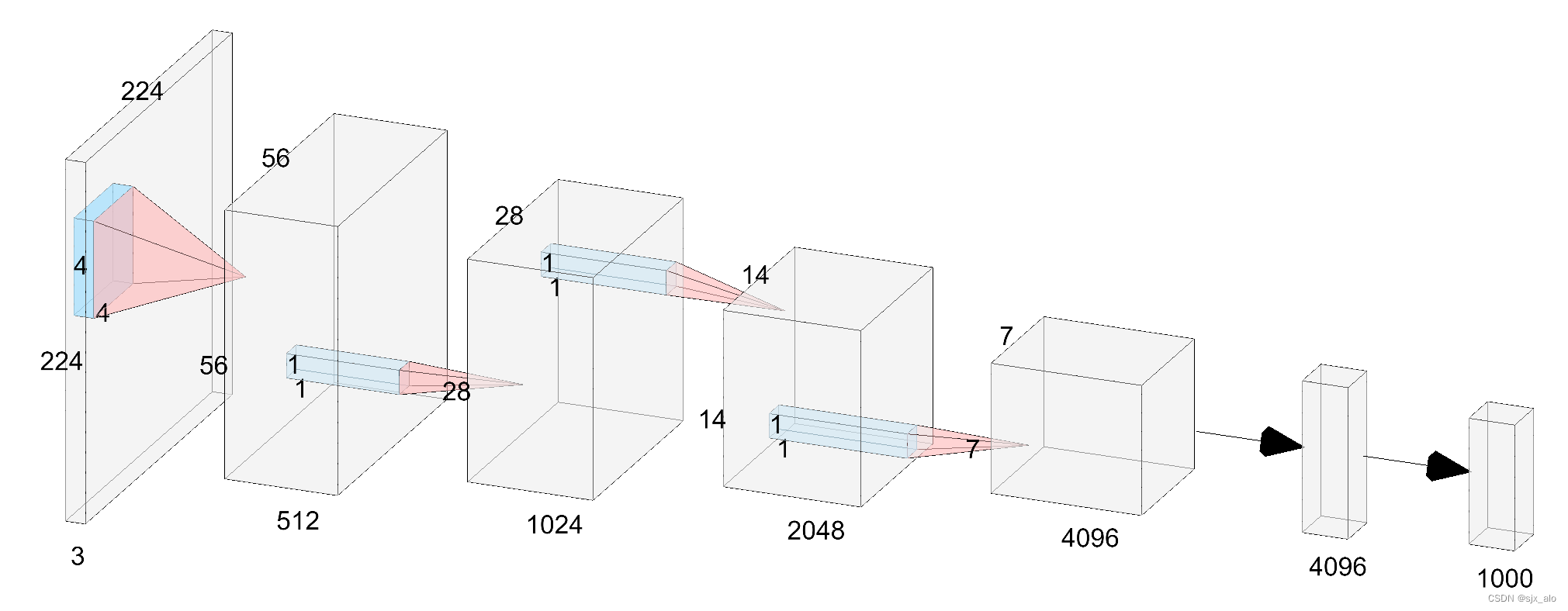
对于第一层卷积层，我们使用步长为4的 $4\times 4\times 3\times C$卷积层，遵循流行设置，将具有3个通道的图像映射到具有C个通道的特征。在第2、3和4层卷积层，使用步幅为2的最大池化层来减小尺寸和特征图，并将通道数依次变为原来的2倍。在第5层卷积层，我们不增加通道数，并使用平均池化层。最后一层是全连接层，输出分类结果。

第2-第5这几个卷积层中，每个卷积核的内核大小为$1\times 1$。这里使用$1\times 1$卷积核的原因是：因为我们的目标是在保留特征图信息的同时对每一层使用最小的计算成本。在每个$1\times 1$卷积层之后应用激活函数。为了简化网络的训练过程，还在每一层之后添加了批量归一化。VanillaNet没有shortcut，因为我们凭经验发现添加shortcut几乎没有提高性能。

虽然 VanillaNet 网络结构简单，容易理解。但是，也带来了一个关键性的问题：网络结构简单导致了弱非线性，而弱非线性导致性能受到限制。 为了解决这一问题，文中作者提出了两种技术来解决该问题。

2. 如何提高简单网络的非线性

为了提高VanillaNet的非线性，文中提出了两种技术：

1. 深度训练策略
2. 基于级数启发的激活函数

2.1 深度训练策略

作者认为，VanillaNet 的瓶颈主要在于由于其层数少带来的非线性差的问题，作者基于此观点，首先提出了深度训练策略来解决这一问题。

针对 VanillaNet 中的一个卷积层，深度训练策略提出将其拆分为两个卷积层，从而增加其非线性，然而，将一层拆分成两层会显著增加网络的计算量和复杂度，因此，作者提出只需在训练时增加网络层数，在推理时将其融合即可。具体来说，被拆分为两层的卷积会使用如下的激活函数：
$$A^{\prime }(x)=(1-\lambda )A(x)+\lambda x$$
是由一个传统非线性激活函数（如 ReLU 等）和恒等映射加权得到。将当前epoch和深度训练epoch的个数分别表示为e和E。我们设置$\lambda =\frac{e}{E}$。在网络训练的初始阶段，$\lambda =0$，非线性激活函数会占主导地位，使得网络在开始训练时具有较高的非线性，在网络训练的过程中，恒等映射的权值会逐渐提升，此时该激活函数会逐渐变为线性的恒等映射，当训练收敛时，我们有$A(x)=x$，这意味着两个卷积层在中间没有激活函数。不具有非线性激活的两个卷积层就可以被融合为一层，从而达到了深层训练，浅层推理的效果。下面，我们进一步演示了如何合并这两个卷积层。

我们首先将每个批处理归一化层及其前一个卷积转换为单个卷积。我们将$W\in R^{C_{out}\times (C_{in}\times k\times k)}$， $B\in R^{C_{out}}$表示为输入通道为$C_{in}$，输出通道为$C_{out}$，核大小为$k$的卷积核的权矩阵和偏置矩阵。批归一化中的$scale$, $shift$, $mean$和$variance$分别表示为$\gamma ，\beta ，\mu ，\sigma \in R^{C_{out}}$。合并后的权重和偏置矩阵为:
$$W_i^{\prime }=\frac{{\gamma }_i}{{\sigma }_i}{W}_i,B_i^{\prime }=\frac{(B_i-{\mu }_i){\gamma }_i}{{\sigma }_i}+{\beta }_i，(2)$$
其中下标$i\in 1,2，\dots ，C_{out}$表示第$i$个输出通道中的值。

在将卷积与批处理归一化合并之后，我们开始合并两个 $1\times 1$ 卷积。分别用 $x\in R^{C_{in}\times H\times W}$ 和 $y\in R^{C_{out}\times H^{\prime }\times W^{\prime }}$ 作为输入和输出特征，卷积可以表示为:
$$y=W\ast x=W\cdot im2col(x)=W\cdot x，(3)$$
其中 $\ast$ 表示卷积运算，$\cdot$ 表示矩阵乘法，$x\in R^{(C_{in}\times 1\times 1)\times (H^{\prime }\times W^{\prime })}$由 $im2col$ 运算导出，将输入转换为与核形状对应的矩阵。幸运的是，对于$1\times 1$卷积，我们发现 $im2col$ 操作变成了简单的重塑操作，因为不需要有重叠的滑动核。

因此，将两个卷积层的权值矩阵分别表示为 $W1$ 和 $W2$ ，两个没有激活函数的卷积表示为:$$y=W1\ast (W2\ast x)=W1\cdot W2\cdot im2col(x)=(W1\cdot W2)\ast x，(4)$$因此，$1\times 1$卷积可以在不增加推理速度的情况下合并。

2.2 基于级数启发的激活函数

深度神经网络提出了深度神经网络提出了几种不同的激活函数，包括最流行的整流线性单元(ReLU)及其变体(PReLU、GeLU和Swish)。他们专注于使用不同的激活函数来提升深度复杂网络的性能，然而，正如现有工作的理论证明，简单和浅层网络的有限功率主要是由较差的非线性引起的，这与深层和复杂网络不同，因此尚未得到充分研究。

实际上，改善神经网络的非线性有两种方法：堆叠非线性激活层或增加每个激活层的非线性，而现有网络的趋势选择前者，导致并行计算能力过剩时的高延迟。

改善激活层非线性的一种直接想法是堆叠。激活函数的串行堆叠是深度网络的关键思想。相反，我们转向并发堆叠激活函数。将神经网络中输入 $x$ 的单个激活函数表示为 $A(x)$，可以是 $ReLU$ 和 $Tanh$ 等常用函数。$A(x)$ 的并发堆叠可以表示为：
$$A_s(x)=\sum _{i=1}^n{a}_{i}A(x+b_i)$$
其中 $n$ 表示堆叠激活函数的数量，$a_i$, $b_i$ 是每个激活的规模和偏置，以避免简单的累积。通过并发堆叠可以大大增强激活函数的非线性。

为了进一步丰富序列逼近能力，我们使用基于序列的函数能够通过改变其相邻的输入来学习全局信息，这与BNET类似。具体来说，给定一个输入特征$x\in {\mathbb{R}}^{H\times W\times C}$，其中 $H$、$W$ 和 $C$ 是其宽、 高和通道的数量，激活函数被表述为：
$$A_s(x_h,w,c)=\sum _{i,j\in -n,n}{a}_{i,j,c}A(x_{i+h,j+w,c}+b_c)$$

其中 h ∈ { 1 , 2 , ⋯   , H } h \in \{1,2,\cdots,H\} h∈{1,2,⋯,H}， w ∈ { 1 , 2 , ⋯   , C } w \in \{1,2,\cdots,C\} w∈{1,2,⋯,C}。很容易看出，当$n=0$ 时，基于序列的激活函数 $As(x)$ 退化为普通激活函数 $A(x)$ ，这意味着所提出的方法可以视为现有激活函数的一般扩展。我们使用ReLU作为基本激活函数来构造我们的系列，因为它对于GPU中的推理非常有效。
我们进一步分析了所提出的激活函数与其相应的卷积层相比的计算复杂度。对于内核大小为 $k$ ，$C_{in}$ 为输入通道和 $C_{out}$ 为输出通道的卷积层，计算复杂度为：
$$O(CONV)=H\times W\times C_{in}\times C_{out}\times k^2$$
而序列激活层的计算成本是：
$$O(SA)=H\times W\times C_{in}\times n^2$$
因此我们有：
$$\frac{O(CONV)}{O(SA)}=\frac{H\times W\times C_{in}\times C_{out}\times k^2}{H\times W\times C_{in}\times n^2}=\frac{C_{out}\times k^2}{n^2}$$

以VanillaNet-B中的第4阶段为例，其中$C_{out}=2048$ ,$k=1$ 和$n=7$ ，比率为84。总之，所提出的激活函数计算成本仍然远低于卷积层。更多的实验复杂性分析将在下一节中展示。

3. 实验

为了证明 VanillaNet 的有效性，作者在计算机视觉的三大主流任务：图像分类、检测和分割上进行了实验。

作者首先验证了提出的深度训练方案和级数激活函数的有效性：

表 1 极简网络在图像分类的性能

从上表中可以看到，所提出的两个方案可以大幅提升 VanillaNet 的精度，在 ImageNet 上有数十个点的提升，此外，作者还在 AlexNet 这种传统网络上也进行了实验，效果提升依旧十分惊艳，这证明了简单的网络设计只要通过精心的设计和训练，仍然具有强大的威力。而对于 ResNet50 这类复杂网络来说，本文提出的设计方案收效甚微，说明这类方案对于简单的网络更为有效。

表 2 极简网络在图像分类的性能

残差模块在 VanillaNet 这种简单的网络中是否还奏效？作者同样针对这一问题进行了实验，实验表明，不管是采用 ResNet 本身的残差方案还是改进后的 PreAct-ResNet 残差方案，对于 VanillaNet 来说都没有提升，这是否说明了残差网络不是深度学习的唯一选择？这值得后续研究者们的思考。作者的解释是由于 VanillaNet 的深度较少，其主要瓶颈在于非线性而非残差，残差反而可能会损害网络的非线性。

接下来，作者对比了 VanillaNet 和各类经过复杂设计的网络在 ImageNet 分类任务上的精度。

表 3 极简网络在图像分类的性能

可以看到，所提出的 VanillaNet 具有十分惊艳的速度和精度指标，例如 VanillaNet-9 仅仅使用 9 层，就在 ImageNet 上达到了接近 80% 的精度，和同精度的 ResNet-50 相比，速度提升一倍以上（2.91ms v.s. 7.64ms），而 13 层的 VanillaNet 已经可以达到 83% 的 Top-1 准确率，和相同精度的 Swin-S 网络相比速度快 1 倍以上。尽管 VanillaNet 的参数量和计算量都远高于复杂网络，但由于其极简设计带来的优势，速度反而更快。

图 2 极简网络在图像分类的性能

图 2 更直观的展示了 VanillaNet 的威力，通过使用极少的层数，在 batch size 设置为 1 的情况下，VanillaNet 可以达到 SOTA 的精度和速度曲线。

表 4 极简网络在检测和分割任务的性能

为了进一步显示 VanillaNet 在不同任务的能力，作者同样在检测和分割模型上进行了实验，实验表明，在下游任务上，VanillaNet 也可以在同精度下具有更好的 FPS，证明了 VanillaNet 在计算机视觉中的潜力。

4. 代码解析

在这个部分解析下相关代码内容。
首先，解析对于论文中较为重要的深度训练策略的公式。对于深度训练策略公式，式中的 $\lambda$ 在代码中用位于 VanillaNet/models/vanillanet.py文件中的Line 139。这里使用act_learn进行定义，具体的定义如下

self.act_learn = 1 

另外， $\lambda$ 的更新如下式所示（位于VanillaNet/main.py 文件中的Line 449 ）：

 act_learn = epoch / args.decay_epochs * 1.0 

另外，在代码中训练部分使用两个卷积结构，中间通过一个激活函数连接。具体代码如下所示：

		#	定义self.stem网络结构
        if self.deploy:
            self.stem = nn.Sequential(
                nn.Conv2d(in_chans, dims[0], kernel_size=4, stride=4),
                activation(dims[0], act_num)
            )
        else:
            self.stem1 = nn.Sequential(
                nn.Conv2d(in_chans, dims[0], kernel_size=4, stride=4),
                nn.BatchNorm2d(dims[0], eps=1e-6),
            )
            self.stem2 = nn.Sequential(
                nn.Conv2d(dims[0], dims[0], kernel_size=1, stride=1),
                nn.BatchNorm2d(dims[0], eps=1e-6),
                activation(dims[0], act_num)
            )
        
        
        #	forward中调用上述定义
        if self.deploy:
            x = self.stem(x)
        else:
            x = self.stem1(x)
            #   act_learn 即为λ
            #   当λ=1时，下面这个激活函数等同于没有
            x = torch.nn.functional.leaky_relu(x,self.act_learn)
            x = self.stem2(x)

最后，基于级数启发的激活函数定义的代码如下所示：

class activation(nn.ReLU):
    def __init__(self, dim, act_num=3, deploy=False):
        super(activation, self).__init__()
        self.deploy = deploy
        self.weight = torch.nn.Parameter(torch.randn(dim, 1, act_num*2 + 1, act_num*2 + 1))
        self.bias = None
        self.bn = nn.BatchNorm2d(dim, eps=1e-6)
        self.dim = dim
        self.act_num = act_num
        weight_init.trunc_normal_(self.weight, std=.02)

    def forward(self, x):
        if self.deploy:
            return torch.nn.functional.conv2d(
                super(activation, self).forward(x), 
                self.weight, self.bias, padding=(self.act_num*2 + 1)//2, groups=self.dim)
        else:
            return self.bn(torch.nn.functional.conv2d(
                super(activation, self).forward(x),
                self.weight, padding=self.act_num, groups=self.dim))

    def _fuse_bn_tensor(self, weight, bn):
        kernel = weight
        running_mean = bn.running_mean
        running_var = bn.running_var
        gamma = bn.weight
        beta = bn.bias
        eps = bn.eps
        std = (running_var + eps).sqrt()
        t = (gamma / std).reshape(-1, 1, 1, 1)
        return kernel * t, beta + (0 - running_mean) * gamma / std
    
    #	switch_to_deploy 是在代码部署时进行调用 训练时不进行使用
    def switch_to_deploy(self):
        kernel, bias = self._fuse_bn_tensor(self.weight, self.bn)
        self.weight.data = kernel
        self.bias = torch.nn.Parameter(torch.zeros(self.dim))
        self.bias.data = bias
        self.__delattr__('bn')
        self.deploy = True

总结

总结来说，VanillaNet 是一种十分简洁但强大的计算机视觉网络架构，使用简单的卷积架构就可以达到 SOTA 的性能。自从 Transformer 被引入视觉领域后，注意力机制被认为是十分重要且有效的结构设计，然而 ConvNeXt 通过更好的性能重振了卷积网络的信心。事实证明，单纯的卷积结构也可以达到SOTA的精度。
最后，如果有什么疑问欢迎在评论区提出，对于共性问题可能会后续添加到文章介绍中。