🚀Write In Front🚀
📝个人主页:令夏二十三
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
📣系列专栏:【数据结构】
💬总结:希望你看完之后,能对你有所帮助,不足请指正!共同学习交流 🖊
文章目录
目录
前言
一、 查找的基本概念
1、在哪里查找?
2、什么是查找?
3、如何显示查找的结果?
4、查找的目的是什么?
5、查找表怎么分类?
6、如何评价查找算法的优劣性?
7、在学习查找算法的过程中,我们要研究的是什么?
二、线性表的查找
1. 顺序查找
1.1 顺序表的类型定义
1.2 顺序查找应用范围
1.3 顺序查找算法
1.4 提高查找效率的方法
1.5 查找算法的优缺点
2. 折半查找
2.1 折半查找算法
2.2 性能分析
编辑
三、树表的查找
1. 二叉排序树
1.1 二叉排序树的查找
1.2 二叉排序树的插入、生成与删除
四、散列表的查找
1. 散列表的基本概念
1.1 基本思想
1.2 散列表的若干术语
2. 散列函数的构造方法
3. 处理冲突的方法
3.1 开放地址法
前言

关于我写这篇文章的原因及目的
我在今年寒假期间就开始看B站王卓老师的《数据结构和算法》课程了,一直想看完并完成这门课的笔记,但是前段时间由于各种其他学科的学习、算法竞赛备赛和人工智能的学习,中断了这门课的笔记记录。
趁现在处于期末复习期间,我打算继续更新这门课的笔记,既能兼顾课内复习,又可以锻炼自己写博客输出的能力,还可供其他小伙伴们阅读学习。
另外,从本篇笔记开始,我会学习各位C站大佬的排版和写作方式(这一篇的排版就很大程度上借鉴了夏目大佬的博客),争取成为一个优秀的博主!
提示:以下是本篇文章的正文内容
一、 查找的基本概念
在前几个章节的学习中,我们探究了数据结构的三大组成部分,也就是数据的存储结构、逻辑结构和数据的运算,我们认识了线性表、树、图等数据结构,学习了它们的各种算法,接下来我们会对其中的查找和排序算法进行进一步的研究。
而这一章要研究的,就是查找算法。我们将通过几个 What、Why、How 来认识查找的基本概念。
1、在哪里查找?
凡是算法,必须要明确它的使用场景,才能实现它的价值,查找算法的使用场景就是查找表。
查找表的定义区别于之前学习的线性表,它更具普适性,线性表可以说是查找表的子集。只要是同一类型数据元素构成的集合,就可以称为查找表,表内元素的关系可以自由设置,因此其应用方式灵活。
2、什么是查找?
查找就是,根据给定的值,在查找表中确定一个其 关键字等于给定值 的数据元素。
这里的关键字是用来标识一个数据元素的某种数据项的值(也可以称作符号)。
| 分类 | 作用 |
| 主关键字 | 唯一地标识一条记录(只对应一个数据元素) |
| 次关键字 | 可用于识别若干记录(用次关键字找具体的数据项) |
3、如何显示查找的结果?
若查找成功,则结果给出整个记录的信息,或给出记录在查找表中的位置;
若查找失败,则结果给出 “空记录” 或 “空指针” 。
4、查找的目的是什么?
- 在不在:查询某个特定的元素是否在表中
- 有没有:检索某个特定元素的各种属性
- 打基础:作为之后将要进行的插入或删除操作的基础
5、查找表怎么分类?
| 类型 | 功能 |
| 静态查找表 | 仅作查询操作 |
| 动态查找表 | 做插入和删除操作 |
6、如何评价查找算法的优劣性?
我们评价查找算法的优劣性的根据,是算法中关键字的比较次数,也就是平均查找长度(ASL,Average Search Length)。
平均查找长度就是关键字比较次数的期望值(查找第i个记录的概率乘以找到它所需的比较次数,再求和):
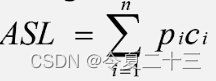
7、在学习查找算法的过程中,我们要研究的是什么?
查找的方法取决于查找表的结构,我们在对算法进行优化之前,就要先研究查找表的存储结构,在集合中的数据元素之间人为地加上某种确定的约束关系,提高查找的效率。
总之,我们要研究的就是查找表的各种组织方法及其查找过程的实施。
作者离期末考只剩两周啦!正在紧张备考中,所以接下来就只是记录一下知识的自用笔记,没有过多的讲解,等到暑假再做一下优化~
二、线性表的查找
1. 顺序查找
1.1 顺序表的类型定义
typedef struct{
KeyType key;//关键字域
}ElemType;
typedef struct{
ElemType *R;//表的基地址
int length;//表长
}SSTable;//Sequential Search Table
SSTable ST;//定义顺序表ST 1.2 顺序查找应用范围
- 顺序表或线性链表表示的静态查找表
- 表内元素之间无序
1.3 顺序查找算法
初始版
int Search_Seq(SSTable ST,KeyType key){
for(int i=ST.length;i>=1;i--)
if(ST.R[i].key==key) return i;
return 0;
}//若查找成功,则返回其位置信息,否则返回0 进阶版(设置监视哨兵,减少比较次数)
int Search_Seq(SSTable ST,KeyType key){
ST.R[0].key=key;
for(i=ST.length;ST.R[i].key!=key;i--)
return i;
}//若查找成功,则i不为0,返回当前i的值 改进前后的顺序查找算法,时间复杂度都为O(n)。
1.4 提高查找效率的方法

1.5 查找算法的优缺点
优点:算法简单,逻辑次序无要求,且不同存储结构均适用。
缺点:ASL太长,时间效率太低。
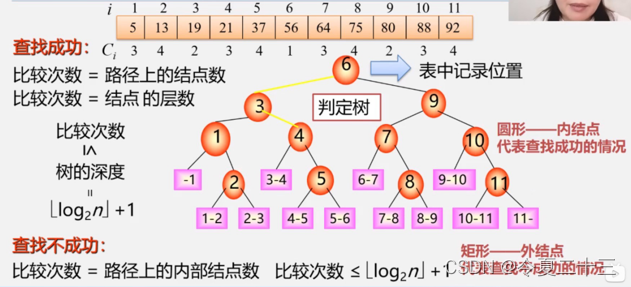
2. 折半查找
又称二分查找,每次将待查记录所在区间缩小一半。
2.1 折半查找算法
int Search_Bin(SSTable ST,KeyType key){
int low =1,high=ST.length;//设置区间两端
while(low<=high){
mid=(low+high)/2;
if(ST.R[mid].key==key) return mid;//找到待查元素
else if(key<ST.R[mid].key) high=mid-1;//继续在前半区间进行查找
else low=mid+1;//继续在后半区间进行查找
}
return 0;//顺序表中不存在待查元素
} 2.2 性能分析
- 优点:效率比顺序查找高。
- 缺点:只适用于有序表,且仅限于顺序存储结构,对线性链表无效。
三、树表的查找
当表的插入、删除操作频繁时,为了维护表的有序性,需要移动表中的很多记录,基于此,我们会使用动态查找表,也就是几种特殊的树,表结构在查找的过程中动态生成。
1. 二叉排序树
二叉排序树又称为二叉搜索树、二叉查找树,其定义如下:
二叉排序树或是空树,或是满足如下性质的二叉树:
(1)若其左子树非空,则左子树上所有结点的值均小于根节点的值;
(2)若其右子树非空,则右子树上所有结点的值均大于等于根节点的值;
(3)其左右子树本身又各是一棵二叉排序树。
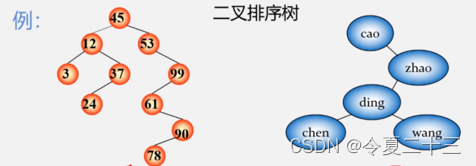
二叉排序树的性质:中序遍历非空的二叉排序树所得到的数据元素序列是一个按关键字排列的递增有序序列。
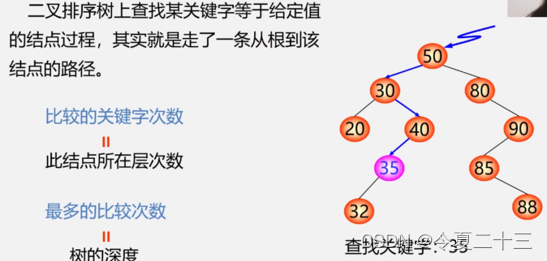
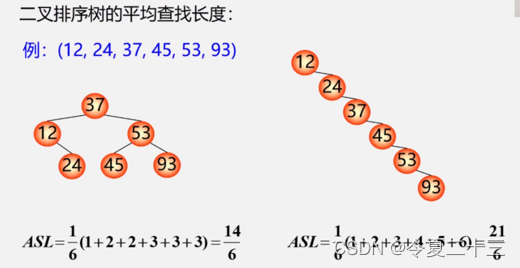
1.1 二叉排序树的查找
算法描述:

算法分析:

1.2 二叉排序树的插入、生成与删除
1.2.1 二叉排序树的插入:

1.2.2 二叉排序树的生成

一个无序序列可通过构造二叉排序树而变成一个有序序列。
插入的结点均为叶子结点,故无需移动其他结点,相当于在有序序列上插入记录而无需移动其他记录。
但需要注意的是,关键字的输入顺序不同,建立的二叉排序树也不同。
1.2.3 二叉排序树的删除
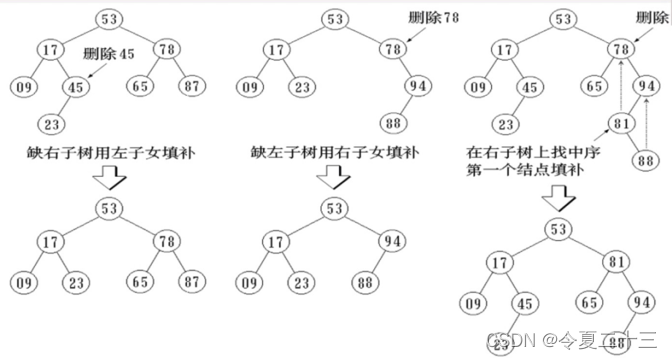
四、散列表的查找
1. 散列表的基本概念
1.1 基本思想
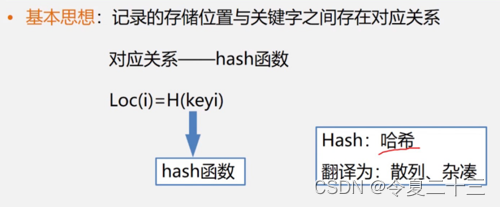
1.2 散列表的若干术语
散列方法(杂凑法)
选取某个函数,依该函数按关键字计算元素的存储位置,并按此存放;
查找时,由同一个函数对给定值k计算地址,将k与地址单元中元素关键码进行比较,确定查找是否成功。
散列函数(杂凑函数)
散列方法中使用的转换函数。
散列表(杂凑表)
按上述思想构造的表。
冲突
不同的关键码映射到同一个散列地址。
同义词
具有相同函数值的多个关键字。
2. 散列函数的构造方法
使用散列表要解决好两个问题:
- 构造好的散列函数
- 制定一个好的解决冲突的方案

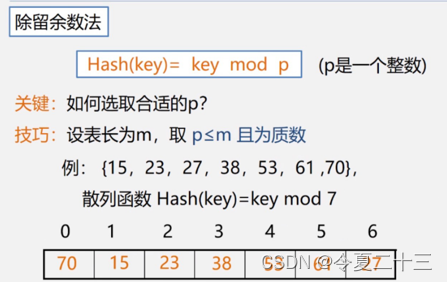
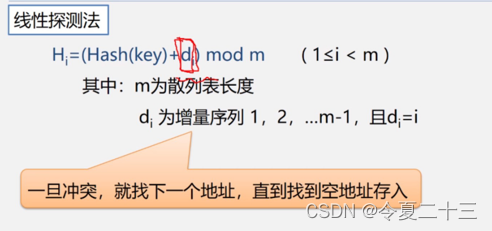
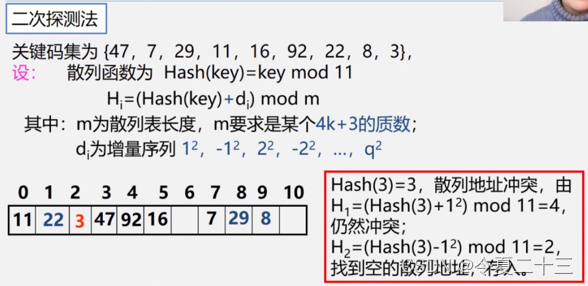
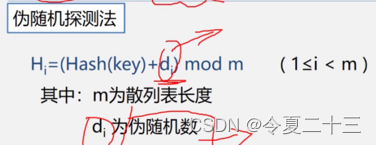
3. 处理冲突的方法
3.1 开放地址法