【递归树】

递归的思想是将大问题分解为小问题，然后再将小问题分解为更小的问题，直到问题的数据规模被分解得足够小，不用继续递归分解为止。如果把这个一层一层的分解过程画成图，其实就是一棵树，可以称之为“递归树”。比如之前在讲递归的时候提到的斐波那契数列的递归实现，如果画成递归树就是下面的样子：

// 斐波那契数列：1、1、2、3、5、8、13、21、34、...
// F(0)=1, F(1)=1, F(n)=F(n-1)+F(n-2)
func getFibonacci(n int) int {
	if n == 1 || n == 2 {
		return 1
	}
	return getFibonacci(n-1) + getFibonacci(n-2)
}

在数据结构与算法07：高效的排序算法中说过归并排序使用的是“分而治之”的思想，每次都将数据规模一分为二，如果画成递归树就是下面的样子：

可以看出来，归并排序的递归树是一棵满二叉树，在二分的过程中的时间复杂度是O(logn)。实际上，对于很多业务场景需要使用“二分思想”的情况下，基本上都可以拆解为二叉树这种数据结构来处理，比如归并排序、快速排序、二分查找、跳表等。

【Trie 树】

Trie树也叫“字典树”，它是一种专门处理字符串匹配的数据结构，用来解决在一组字符串集合中快速查找某个字符串的问题。如果要快速查找某个字符串是否在指定的字符串仓库中，除了O(n)时间复杂度的全部遍历方法之外，还可以用Trie树来高效的解决这个问题。

Trie 树是利用字符串之间的公共前缀将重复的前缀合并在一起，比如现在需要在 city、cat、car、door、dog、deep 这几个单词中快速查找某个单词是否存在，就可以把这几个单词组织成一个Trie树，如下所示：

Trie 树有以下特点：

使用多叉树来表示，比如上面查找单词的Trie树的第一层使用26叉树来存储26个英文字母；
根结点不包含字符，除根结点外每一个结点都只包含一个字符；
查找某个单词的时候，就把根结点到某一个叶子结点的路径上经过的字符连接起来，如果一直到叶子结点还不匹配，那就是没找到；
创建Trie树的过程需要扫描所有字符串，因此创建的时间复杂度是O(n)，n表示所有字符串长度之和；
查找字符串的时间复杂度是 O(k)，k 表示要查找的字符串的长度；

使用Go语言实现一个Trie树的代码如下（点此查看源代码）：

package main

import (
	"fmt"
)

// Trie树结构体
type TrieNode struct {
	Data  byte               //存储字符数据
	Next  map[byte]*TrieNode //下一个节点指针
	IsEnd bool               //是否到达叶子结点
}

// Trie树根节点
type TrieRoot struct {
	Len  int //字符个数
	Node map[byte]*TrieNode
}

// 初始化一个Trie树,并给根节点赋值
func NewTire() TrieRoot {
	tRoot := TrieRoot{
		Len:  0,
		Node: make(map[byte]*TrieNode),
	}
	return tRoot
}

// 插入字符
func (tn *TrieRoot) insert(str string) {
	cur := tn.Node
	//循环遍历单词的每个字符
	for i := 0; i < len(str); i++ {
		if cur[str[i]] == nil {
			newNode := &TrieNode{
				Data:  str[i],
				Next:  make(map[byte]*TrieNode),
				IsEnd: false,
			}
			cur[str[i]] = newNode
		}
		//判断是否到达叶子结点
		if i == len(str)-1 {
			cur[str[i]].IsEnd = true
		}
		cur = cur[str[i]].Next
	}
	tn.Len++
}

// 查找字符
func (tn *TrieRoot) find(str string) bool {
	if tn.Node == nil {
		return false
	}
	cur := tn.Node
	//循环遍历单词的每个字符
	for i := 0; i < len(str); i++ {
		//如果某个字符不存在，直接返回false
		if cur[str[i]] == nil {
			return false
		}
		if cur[str[i]].Data != str[i] {
			return false
		}
		if i == len(str)-1 {
			//判断最后一个比较的字符是否到达叶子结点,如果不需要精确匹配就去掉这个判断
			if cur[str[i]].IsEnd == true {
				return true
			}
		}
		cur = cur[str[i]].Next
	}
	return false
}

func main() {
	tire := NewTire()
	tire.insert("city")
	tire.insert("cat")
	tire.insert("car")
	tire.insert("door")
	tire.insert("dog")
	tire.insert("deep")
	fmt.Println("字符串数量：", tire.Len) //6

	fmt.Println(tire.find("cat")) //true
	fmt.Println(tire.find("ca"))  //false,因为是精确匹配
	fmt.Println(tire.find("cd"))  //false
}

上面代码中查找的时候使用的精确匹配，也就是判断到达叶子结点才算匹配完成，如果要实现前缀匹配，比如在“cat”中查找“ca”，就把查找方法中的 if cur[str[i]].IsEnd == true {} 条件去掉即可。

想一想，手机输入法的自动补充词语，和搜索引擎的关键词自动补全，是不是和这个很类似：

【B+树】

我之前在 MySQL底层数据结构的深入分析这篇文章中大概分析了B树和B+树，B树是⼀种多叉平衡查找树，而且⾮叶⼦节点和叶⼦节点都会存储数据；B+树是只有叶⼦节点才会存储数据。这里的 B 一般被解读为 balance，也就是平衡树。

在MySQL中查询数据的时候，通过索引可以让查询数据的效率更高，这是关注的时间复杂度；同时在存储空间方面希望索引不要消耗太多的内存空间，这是关注的空间复杂度。如果使用二叉搜索树作为数据库的索引，会导致一颗数据库索引树太过“高”和“瘦”，如果把树存储在硬盘中，那么每个节点的读取访问都对应一次磁盘 IO 操作，树的高度就等于每次查询数据时磁盘 IO 操作的次数。比起内存读写操作，磁盘 IO 操作非常耗时，所以应该减少磁盘 IO 操作，降低树的高度。如果把二叉树改造成M叉树(M>2)，高度自然会变低，如下图所示的二叉树变成五叉树：

M叉树虽然比二叉树低，但是M也不能太大，因为不管是内存中的数据还是磁盘中的数据，操作系统都是按页（一页大小通常是 4KB）来读取的，一次读取一页的数据，如果要读取的数据量超过一页的大小，就会触发多次 IO 操作。所以在选择M大小的时候，要尽量让每个节点的大小等于一个页的大小，这样的话读取一个节点只需要一次磁盘 IO 操作。

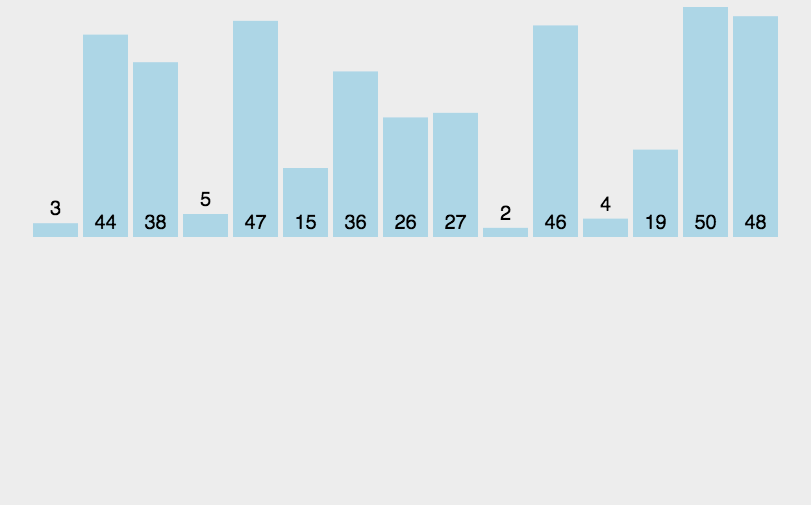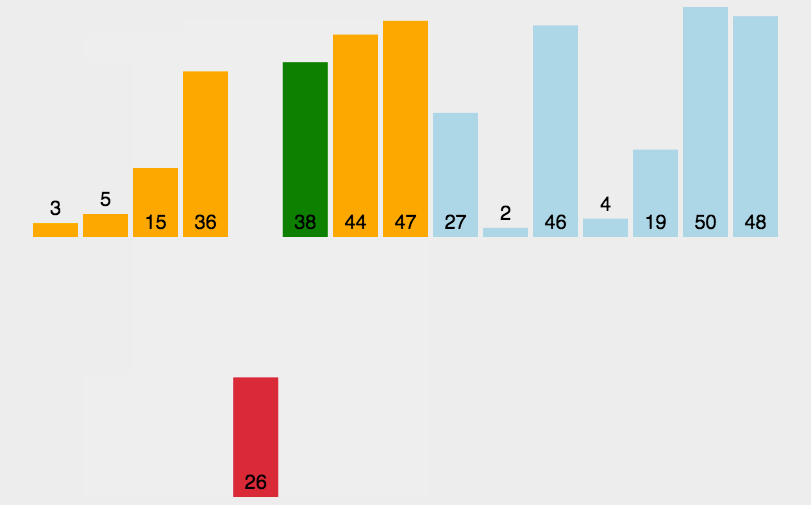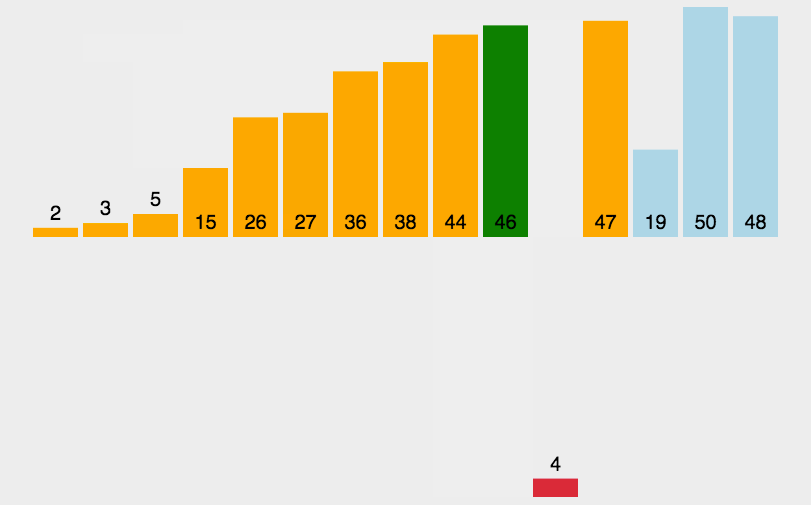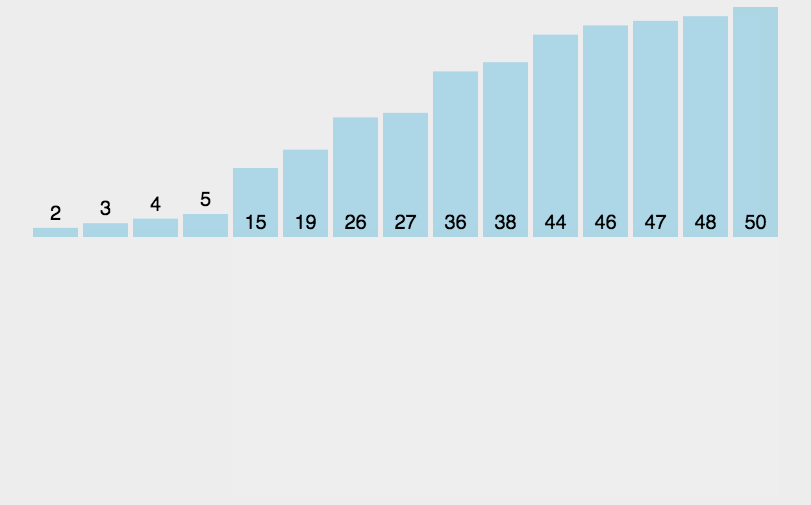
MySQL使用的B+树是从B树演化而来的，而B树是从多叉树演化而来的，对于一个B+树来说，M的值是根据页的大小事先计算好的，每个节点最多只能有M个子节点。在往数据库中写入数据的时候有可能使索引中某些节点的子节点个数超过M，从而导致这个节点的大小超过了一个页的大小，读取这样的节点就会导致多次磁盘 IO 操作。对于这种情况，B+树会将这个节点分裂成两个节点，对于父节点也这样操作，一直影响到根节点。这就是一个由下到上的分裂过程，如下面的动画：

B+树生成过程

这里总结一下 B+树的特点：

每个节点中子节点的个数不能超过M，也不能小于 M/2；
M叉树只存储索引，并不真正存储数据，有点类似跳表（关于跳表参考：数据结构与算法05：跳表和散列表）；
通过链表将叶子节点串联在一起，这样可以方便按区间查找；
一般情况下，根节点存储在内存中，其他节点存储在磁盘中。

【每日一练：最长公共前缀】

力扣14. 最长公共前缀

编写一个函数来查找字符串数组中的最长公共前缀。如果不存在公共前缀，返回空字符串 ""。

示例 1：输入：strs = ["flower","flow","flight"]，输出："fl"
示例 2：输入：strs = ["dog","racecar","car"]，输出：""，解释：输入不存在公共前缀。

（点此查看源代码）

思路1：先计算数组中最短的字符串长度，在这个长度范围内，从头比较数组中每一个字符串相同位置的字符是否都相同。空间复杂度 O(1)，时间复杂度 O(S)，S 是所有字符串中字符数量的总和。最坏情况下，输入数据为n个长度为m的相同字符串，会进行 S = m * n 次比较；最好的情况下，只需要进行 n * min(Len(N)) 次比较，其中 min(Len(N)) 是数组中最短字符串的长度。

func longestCommonPrefix1(strs []string) string {
	length := len(strs)
	if length == 0 {
		return ""
	}
	minLen := len(strs[0])
	tmp := 0
	for i := 1; i < length; i++ {
		tmp = len(strs[i])
		if tmp < minLen {
			minLen = len(strs[i])
		}
	}
	result := ""
	for j := 0; j < minLen; j++ {
		for k := 0; k < length-1; k++ {
			if strs[k][j] != strs[k+1][j] {
				return result
			}
		}
		result += string(strs[0][j])
	}
	return result
}

func main() {
	fmt.Println(longestCommonPrefix1([]string{"flower", "flow", "flight"})) //fl
	fmt.Println(longestCommonPrefix1([]string{"dog", "racecar", "car"}))    //""
}

思路2：依次假设最长公共前缀长度为0到len(strs[0]) ，在每一轮循环中只要strs中存在比当前最长公共前缀(LCP)长度更短的字符串，或者strs中存在和当前 index 字符不相同的字符串，就返回上一轮的最长公共前缀，如果一直没返回，说明strs[0]就是最长公共前缀。时间复杂度: O(N * len(strs(0))，空间复杂度: O(1)。

func longestCommonPrefix2(strs []string) string {
	if len(strs) == 0 {
		return ""
	}
	for i := 0; i < len(strs[0]); i += 1 {
		for _, str := range strs {
			// 只要strs中存在比当前长度i更短的string，立刻返回上一轮LCP，即strs[0][:i]
			// 只要strs中存在当前index字符与LCP该index不相同的字符串，立刻返回上一轮LCP，即strs[0][:i]
			if len(str) <= i || strs[0][i] != str[i] {
				return strs[0][:i]
			}
		}
	}
	return strs[0] // 如果一直没返回，说明strs[0]本身就是LCP，返回它
}

func main() {
	fmt.Println(longestCommonPrefix2([]string{"flower", "flow", "flight"})) //fl
	fmt.Println(longestCommonPrefix2([]string{"dog", "racecar", "car"}))    //""
}