一、引言

1、主要任务

解决信息的保密性和可认证问题，保证信息在生成、传递、处理、保存的过程中，不被未授权者非法地提取、篡改、删除、重放和伪造等。

2、分支

• （1）密码编码学
  对信息进行编码实现屏蔽信息的一门学问，目的是寻求保护信息的保密性和认证性的方法。

• （2）密码分析学
  研究分析破译密码的学问，目的是研究加密信息的破译或消息的伪造。

3、密码体制分类

• （1）对称密码体制
  一对加密和解密算法使用的密匙相同，或实质上等同，即从一个密钥可以很容易地得出另一个密钥。
  （优点）
  具有很高的保密强度，可以达到经受GJ级破译力量的分析和攻击。一些常用的对称加密方法明显地快于任何当前可以使用的双钥加密方法。
  （简化）
  信息安全性高、加解密速度快、密文信息冗余小。
  （缺点）
  它的密匙必须通过安全可靠的途径传输，密钥管理或为影响系统安全性的关键因素，使他难以满足系统的开放性要求。

• （2）非对称加密体制
  加密和解密算法使用的密钥不同，而且对于非授权者来说，他很难从一个密钥得到另一个密钥。
  （优点）
  增加了私钥的安全性，密钥管理问题相对简单，可适用于开放性环境。
  （简化）
  管理简便、代价低、数字签名和认证。
  （缺点）
  保密强度的人为控制力度不如对称密码体制的水平，且加密速度也不如单钥加密算法快，尤其是数据量较大时。

• （3）混合加密体制
  

4、攻击密码系统

• （1）穷举法
  对截收到的密文依次用各种可解的密钥试译，直到得到有意义的明文；或在不变密钥下，对所有可能的明文加密直到与截获密文一致为止。

• （2）分析法
  

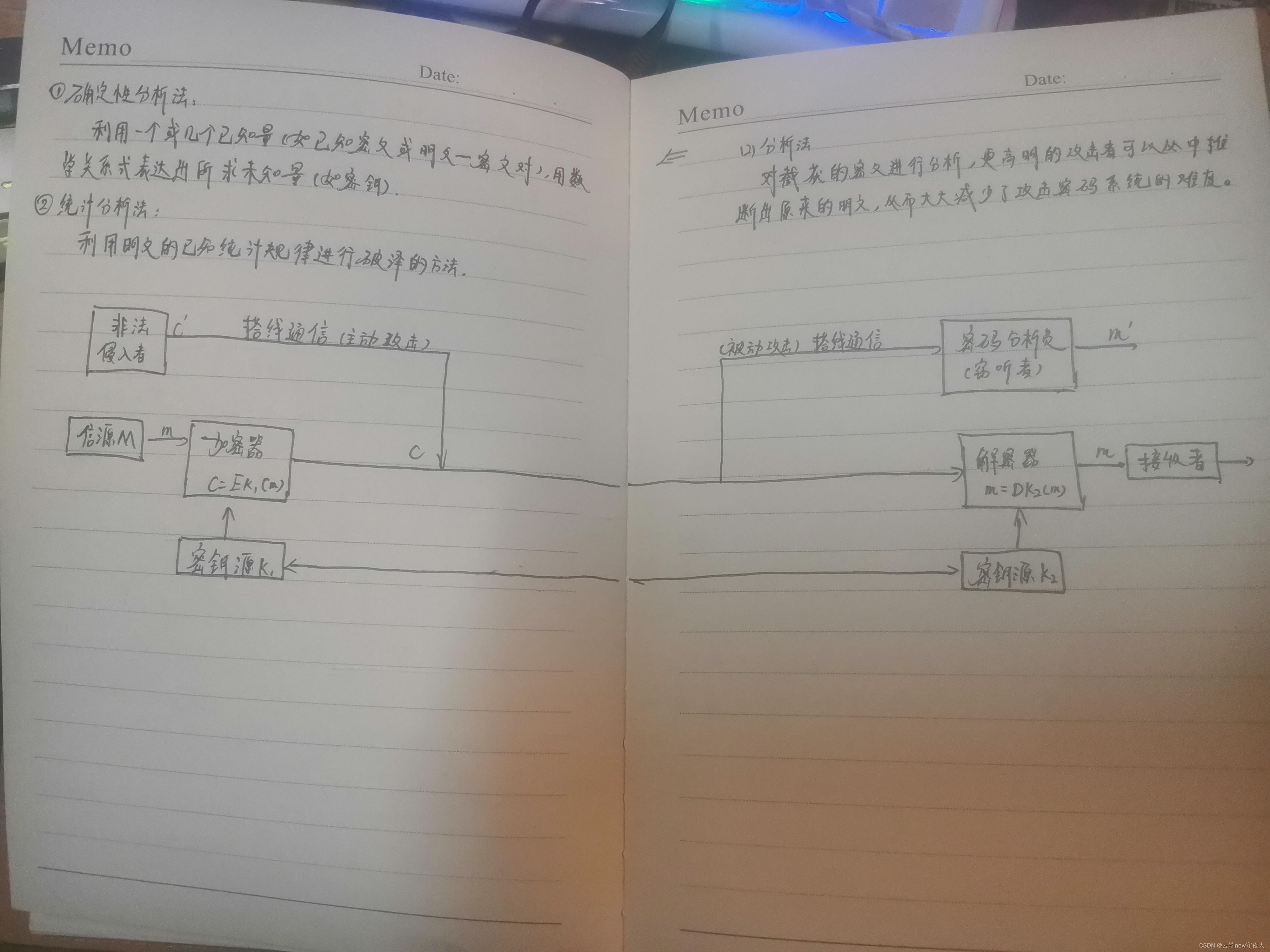
二、普莱费厄体制

1、构造字母表，设为密钥矩阵

• 密钥矩阵

以Char字符中33~122为例

• 代码

	// char字符值范围
	private int MIN = 33, MAX = 122;
	// 密匙数组的规格
	private int X = 10, Y = 9;
	
	/**
	 * 生成密匙key
	 */
	public char[][] GenerateKry() {
		// 一个随机数，以Array_X为随机，Array_Y为自增
		// 目的减少循环出错
		char[][] key = new char[X][Y];
		// 生成数组
		for(int i = 0, z = 1;i < X; i++) {
			for(int j = 0; j < Y; j++, z++) {
				key[i][j] = (char) (32 + z);
			}
		}
		// 得到随机数函数
		Random r = new Random();
		// 数组 --> 乱序密匙
		for(int i = 0 ; i < X ; i++) {
			for(int j = 0 ; j < Y ; j++) {
				// 获取两个个随机数
				int z = r.nextInt(X-1);
				int y = r.nextInt(Y-1);
				// 与 key[i][j]进行调换顺序，从而打乱二元数组
				char temp = key[i][j];
				key[i][j] = key[z][y];
				key[z][y] = temp;
			}
		}
		return key;
	}

2、设立加密方法

	// 密匙变化方向，顺时针，从左上角开始 CHANGE
	private int[][] CHANGE = {{-1,-1},{-1,0},{-1,1},{0,1},
			{1,1},{1,0},{1,-1},{0,-1}};
			
	public int[][] RuleDefinition() {
		// 加密规则
		int[][] rule = new int[3][2];
		// 规则一：当明文对处于同一行时，取明文字母的左边
		rule[0] = CHANGE[7];
		// 规则二：当明文对处于同一列时，取明文字母的上边
		rule[1] = CHANGE[1];
		// 规则三：当明文对既不处于同一行，又不处于同一列时，取明文字母的右下角
		rule[2] = CHANGE[4];
		return rule;
	}

3、加密解密

public String JudgeXAndY(char[][] key, char[] mwd, boolean index) {
		// 获取明文对的相对位置关系,并根据规则修改位置
		// 如果int = 0 就是同行 1就是同列 2就是不同
		int[][] x_y = new int[2][2];
		int temp = 2;
		for(int i = 0;i < X;i++) {
			for(int j = 0;j < Y;j++) {
				for(int z = 0;z < 2;z++) {
					if(key[i][j] == mwd[z]) {
						x_y[z][0] = i;
						x_y[z][1] = j;
					}
				}
			}
		}
		if(x_y[0][0] == x_y[1][0]) {
			temp = 1;
		} else if(x_y[0][1] == x_y[1][1]) {
			temp = 0;
		}
		// 获取当前规则
		int[] rule;
		if(!index) {
			rule = this.RuleDefinition()[temp];
		} else {
			rule = this.BackRuleDefinition()[temp];
		}
		x_y = this.RuleMove(x_y, temp, rule);
		return String.valueOf(key[x_y[0][0]][x_y[0][1]]) + key[x_y[1][0]][x_y[1][1]];
	}

4、字典集合

	public Map<String, String> Encryption(String plaintext) {
		// 明文加密
		// 生成一个随机密匙
		char[][] key = this.GenerateKry();
		// 明文转换
		char[] array_pl = plaintext.toCharArray();
		// 密文
		String keyText = "";
		for(int i = 0;i<array_pl.length-1;i = i+2) {
			char[] mwd = {array_pl[i],array_pl[i+1]};
			keyText += this.JudgeXAndY(key, mwd, true);
		}
		// 判断明文的位数是否为奇数
		if (array_pl.length%2 == 1) {
			keyText += array_pl[array_pl.length - 1];
		}
		// 切割密匙  key --> key1 and key2
		String compressKey = this.CompressKey(key);
		Map<String, String> map = new HashMap<String, String>();
		map.put("key", compressKey);
		map.put("key1",compressKey.substring(0,compressKey.length()/2));
		map.put("key2",compressKey.substring(compressKey.length()/2,compressKey.length()));
		map.put("keyText", keyText);
		return map;
	}

5、结果