目录
浮点型存储的规则
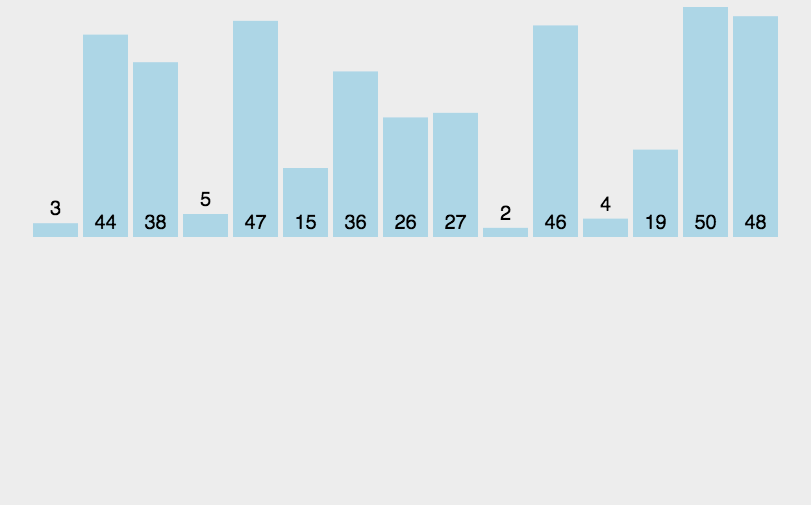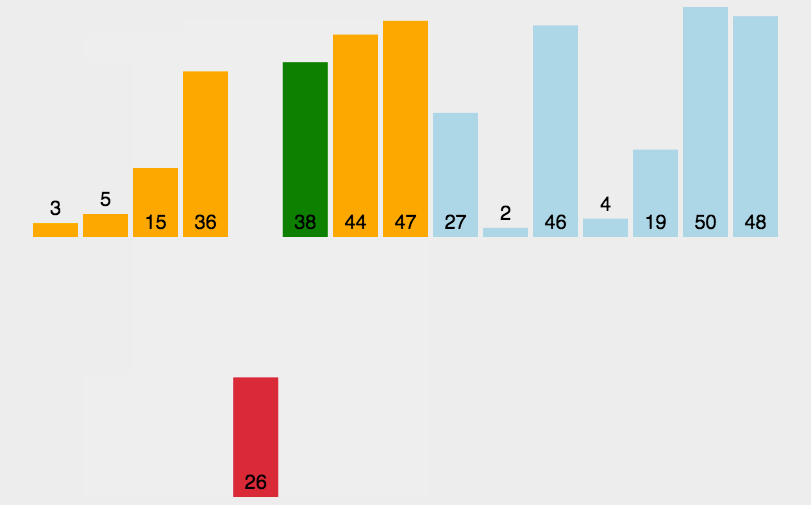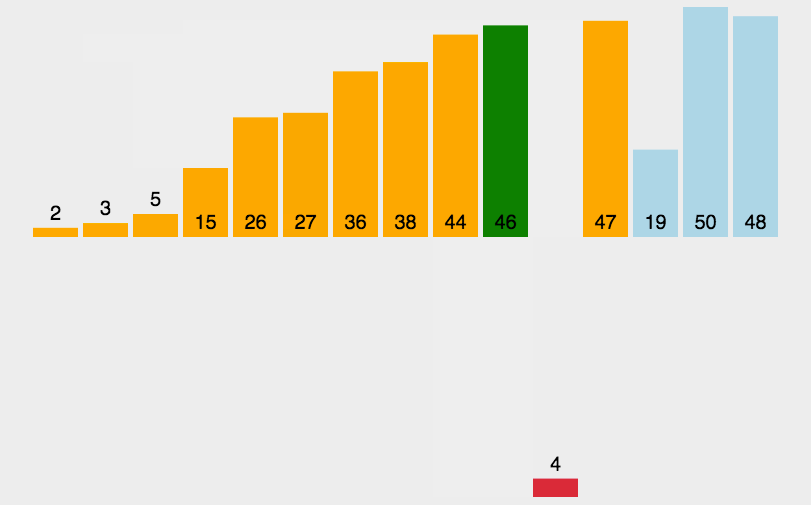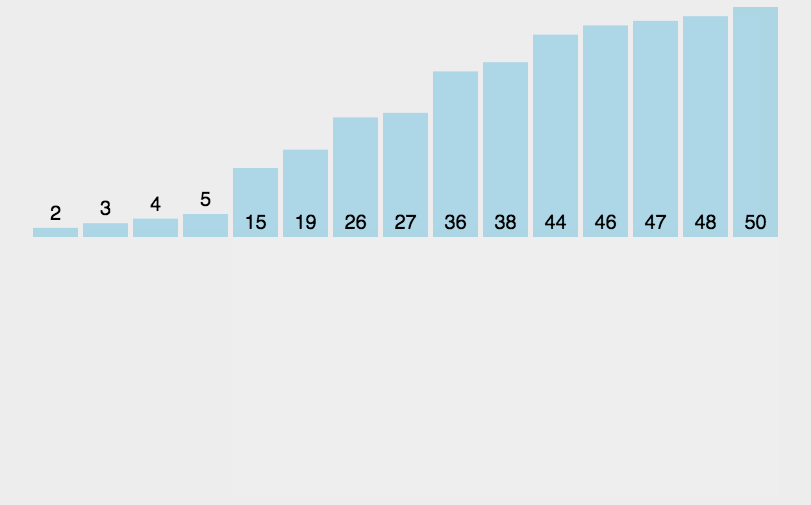
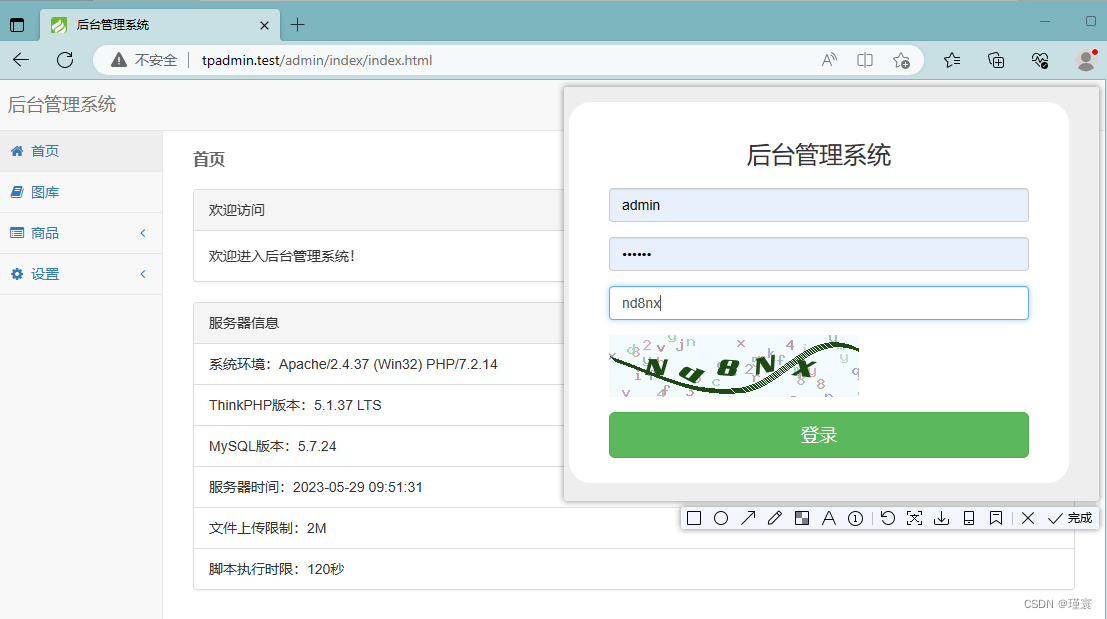
1.前面我们已经学过了整形在数据中的存储是以原码,反码,补码的形式在内存中存储的,那么浮点数是以什么样的形式存储的呢?
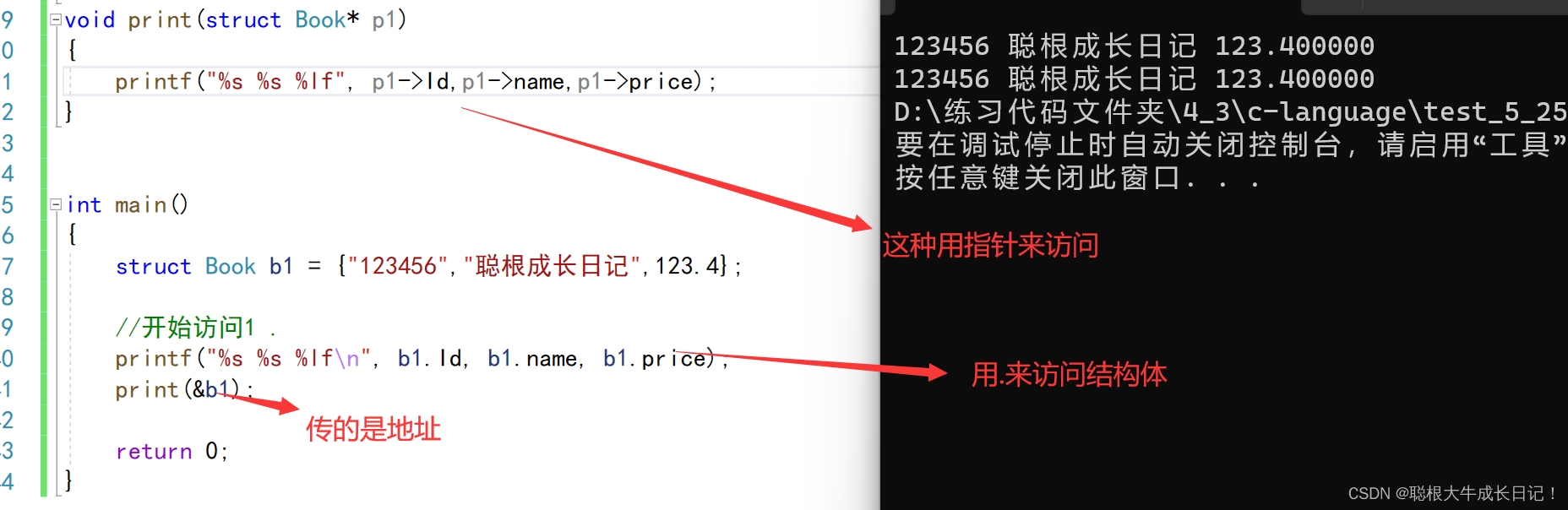
接下来我们通过一段代码来观察——>
int main()
{
int n = 9;
float* p = (float*)&n;//强制类型转换为float*
printf("%d\n", n);//直接打印n
printf("%d\n", *p);//通过指针解引用来打印
*p = 9.0;
printf("%d\n", n);
printf("%f\n", *p);
return 0;
}我们将这段代码放在vs中运行得到以下的结果:

从这里我们不难看出浮点型在内存存储肯定与整形在内存的存储不一样,如果都是以原码,反码,补码的形式存储,他们打印的结果应该是9 9.000000 9 9.000000
所以接下来让我们来深度分析浮点数在内存中存储的情况:>
首先根据国际标准(IEEE754)规定的,任意一个浮点数在内存中二进制的存储公式为:>
f = (-1)^S*M*2^E
其中(-1)^S表示符号位,M表示有效数字,它的范围是:M>=1&&M<2,
2^E表示指数位
就比如说:
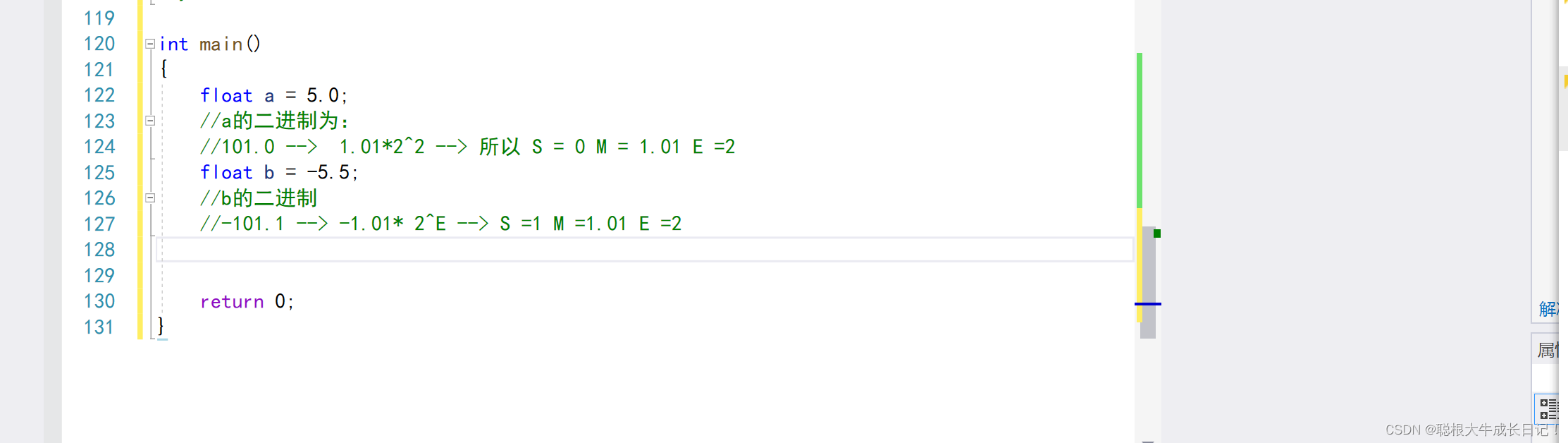
通过上面的我们大概知道如何将一个浮点型的数的二进制如何算出来了,只有能够把浮点数的二进制算出来我们才可以弄懂浮点数在内存中存储的位数

也就是说对于32位的浮点数即float型的变量来说它是 给1个比特位来存储S,这里也不是很难理解因为S的大小也就是1或者是0,而给了8个比特位来存放E的值,又因为我们默认E的值是无符号的,所以实际在内存中存储的时候我们还要给E加上127,然后剩下的M我们用23个比特位来存储M的值。
对于64位的小数我们不相同,它的存储模型为:>

它的位数的分配:S(1bit) E(11bit) M (52bit) ,所以浮点数用来存放小数的时候范围更加精确,因为它又52个比特位用来存放有效数字
对于S来说它与单精度的存储模型没有什么区别,当对于E来说却有区别,在我们计算出来E的之后,实际上内存中存储的是E的值然后在加上1023。
这个E相当于中间数,用来确保我们E的值是无符号的。
接下来我们来讲3种情况下
1:当E的不全为0或者不全为1的时候
我们就可以使用上面的规则来算出浮点数在内存中的存储,然后在求出对应的值。
2:当E全为0的时候,我们知道实际上E的值应该是-127,这个时候我们将M的值前面一个有效位数字改为0,就是0.xxxxxx然后当我们使用公式来算的时候 E^-127,且M的值还为0.xxxxxx,所以它是一个非常小的数字,接近于0
3:当E的值全为1的时候,实际上E的值为128,所以是一个很大的数字接近于无穷大。
补充一下:实际上我们的M存放了24个有效数字,以为前面的一位要么是0或1。
有了以上知识我们就可以来解决我们一开始提出的问题了,并且解释为啥会出现那样的原因。


本章完,谢谢大家的观看,让我们一起进步把!