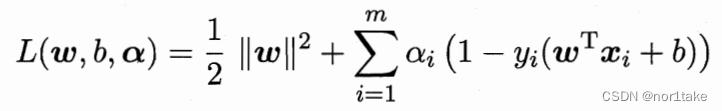传统图形学对nerf的对比与应用落地

作者今年参加了China3DV的盛会，大会的发表、线下讨论、学者、工业界等等的交流着实对于Nerf有了更深的思考，以下是作者的抛砖引玉，如有不当之处敬请指出~

传统图形学与nerf的简介：

传统图形学：显示表达几何表达方式：网格（Mesh）、点云（Point cloud）、体素（Voxel）、隐式函数（Implicit），渲染主要包括两种：1、渲染管线（主实时）；2、光线追踪（主离线，现也出现PC的实时光追）
在这里插入图片描述

nerf:nerf本质上提供了一种新的逆渲染方式，通过神经网络模拟连续的场+体渲染的方式。同时也是隐式可微渲染，创造性的引进神经网络达到惊艳的效果。

nerf的基本原理：

NeRF函数是（一）将一个连续的场景表示为一个输入为5D向量的函数，包括一个空间点的3D坐标位置，以及roll, pitch, yaw中的 pitch, yaw视角方向，其中roll翻转角不需要因为转动翻转角的渲染结果是一样的！输出结果中包括空间点的3D位置（或者说是体素）的密度、视角相关的该3D点颜色。以空间坐标或者其他维度（时间、相机位姿等）作为输入，通过一个MLP网络模拟目标函数，生成一个目标标量（颜色、深度等）的过程（二）基于经典的Volume rendering提出了一种可微渲染的流程，包括一个层级的采样策略。（三）提出了一种位置编码（positional encoding）将5D坐标映射到高维空间。
如下图是输入输出整体流程：
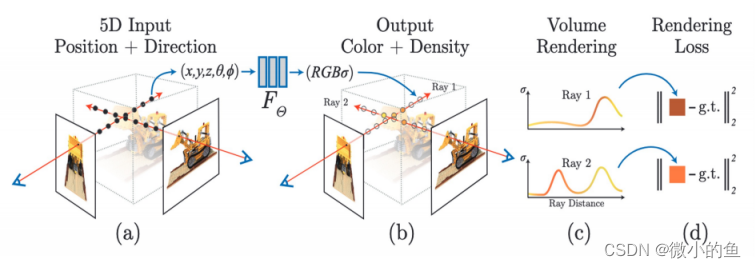
在这里插入图片描述

可微渲染

从二维图片中得到三维场景信息的渲染方式有一个名称叫——逆向渲染（inverse rendering），可微即计算渲染过程的导数。可微渲染就是实现逆向渲染的一个方法，可微即计算渲染过程的导数。对于Nerf来说，由于体渲染可微、坐标空间变换也可微，所以Nerf也是可微，即Nerf是可微渲染的一种，只是nerf是基于隐式表达+体渲染的可微渲染！可微隐式表达常有Nerf、SDF、occupancy field。

可微需要两个前提：

准备参考目标图片 A：二维目标图片；可微渲染的目标就是使得渲染的结果无限接近这张参考图片，并且找到能够生成这张图片的3D 场景B。
初始3D 场景 B’参数：可以是一个大致接近于真实场景的粗略的三维场景，也可以是完全随机的三维场景

。
在这里插入图片描述

1. 拿着个B’ 送到渲染器中,渲染得到图片 A’
2. 这一步就是和神经网络类似了，比较 A 和 A’ 的差别，计算出Loss
3. 将 Loss Backprop 到场景B’ 中的不同参数上，比如材质参数，镜头参数，修改这些参数的值，获得新的场景 B1’
4. 和训练神经网络一样，继续 1-3 这个过程。
可微渲染包括两方面：1、前向渲染：根据场景参数渲染出一张二维图片；2、逆向传播：将前向渲染结果与A做比较得到loss，再将梯度反向传播到场景参数中，实现优化；其中步骤3就是可微分渲染的的关键部分,因为这一步需要算梯度Gradient。Nerf的创新主要逆向渲染中是引进深度学习的神经网络去处理3这部分的梯度Gradient；前向渲染使用了拍照，借助一些工具，比如colmap处理成一些参数，再送到神经网络里。

体渲染

体积数据被保存在3D纹理中，采样时进行三线性插值,这种方法被称为体素重建。体素信息会决定光的传播。体渲染主要是指通过追踪光线进入场景并对光线长度进行某种积分来生成图像或视频，具体实现的方法包括：Ray Casting，Ray Marching，Ray Tracing。

所以体渲染相比于传统的Mesh、Point，更加适合模拟光照、烟雾、火焰等非刚体因为这些是很难用几何体表现的。因为体渲染是一种可微渲染，非常适合与基于统计的深度学习相结合。
体渲染（Volume）原理：光线可以在物体内部进行散射，将3D体积数据隐式提取出来，使用体素表示，它是体渲染的最小单元，表示场的3D空间某部分的值。当光线穿越体素立方体时采样，并对每次得到的采样数据进行反复累加这种方法使用光学模型来映射体积数据并且通过摄像机发出的视线累积光照结果。累加简单来说就是当光线穿越体素立方体时对光进行等距采样，并对每次得到的采样数据进行反复累加使用混合公式：

根据射线几何公式：在这里插入图片描述
，O是原点，d是方向，t是在d方向上行进的距离,更改t的值可以定义沿射线的任何位置。

体渲染

采样（Sample），图形学中常见的采样求近似积分就黎曼和与蒙特卡洛。黎曼和：在（a,b）区间划分N等份，长度L=b-a/N,在每一份取一位置代表一小份的均值，这样的积分就是黎曼和，缺点也很明显收敛慢。相同采样数下蒙特卡洛优与黎曼和。蒙特卡洛简单来说就是根据方差来采样，方差大有更多的采样反之则小（重要性采样），就有了重要性采样与分层采样，nerf也有使用分层采样。分层采样简单来说就是一种降低方差的方法，把积分区间S分成几个较小区域Si,并把Si上积分的总和作为积分的值。
所以最终的体渲染公式：
在这里插入图片描述
理论上，我们可以对这条射线经过空间上的每个点的密度（只和空间坐标相关）和颜色（同时依赖空间坐标和入射角）进行某种积分就可以得到每个像素的颜色。当每个像素的颜色都计算出来，那么这个视角下的图像就被渲染出来了。为了解决传统图形学使用巨大的查表获取RGB和密度，Nerf采用神经网络来，建模辐射场，这样无论空间有多大，不影响我们表示辐射场的所需要的存储量，而且这个辐射场表示是连续的。

传统图形学与Nerf对比：

传统图形学：
1.显示表达事先设计好后渲染、纹理贴图、材质、几何模型表达（Mesh、cloud point、体素）、场景、光照等等可编辑、可控。
2.现应用在各大工业、影视动画、娱乐游戏、VR/AR等等行业，提供了一套可编辑、并且有大量的工具、开源的成熟项目，能做到渲染大规模、特大规模的城市、移动端等等很成熟的一套体系。
3.实时全局光线（GI）、次表面散射比如SSS、PBR材质的可编辑，多光源、复杂场景的遮挡关系、除了静态model的渲染还有动态的model，比如基于动画、物理的动画这些是Nerf无法解决的，或者说有待研究的！
全局光照

nerf：
1.是隐式表达，端到端的渲染，不解耦，无法拆分纹理、材质、场景、等等，更无法编辑，而且Nerf现在只支持静态的场景内，动态场景不支持！
2.工具链不成熟许多问题还有待进一步的研究、解决、突破等等、nerf现状未落地、学术界好发paper，抢肉吃，先把之前在传统图形学的搬到nerf或者引进nerf的方式（由于比较新生态处于萌芽的爆发期比较混乱）。
3.性能还不能实时。现已只能在服务器上运行，移动端app做拍照图片输入，服务器输出三维模型到移动端上运行，就算是英伟达的算法最快也需要10分钟以上才可以生成对应的渲染。
4.对于nerf 的未来大会中的老师也有做了几点预测包括可能是nerf、AICG、数字人、新三维重建（可能为传统图形学服务）；共识是为渲染与重建提供了一种新方法与工具等。

nerf效果

nerf的第一个产品-Luma AI

全球现已知的第一家nerf尝试落地产品的公司，3D内容方案商Luma AI，近期宣布完成了2000万美元的A轮融资，本轮融资由Amplify Partners领投，NVIDIA(NVentures)、General Catalyst跟投。
尤其该公司在23年AIGC非常火热流行的大背景下，Luma AI也加入文字、nerf图片生成3D模型。此外近期也加入AR的预览功能，在IPhone上直接预览nerf生成的3D模型。
Luma官网
YouTube
Luma AI在2022年底发布通过iPhone进行3D场景捕捉，并且融入NeRF能力，同时也可利用LiDAR实现更精准识别。APP只支持IOS，并且要求iPhone11及其以上OS版本在16.0及其以上。
场景捕捉、本地图片/视频上传、新视角渲染等功能需要联网使用，其中Luma AI在新视角渲染时支持调整焦距、视角和画面比例等功能，一键导出渲染mp4视频。除此之外，在模型训练好后，场景Mesh模型及固定视角的渲染图像被加载到移动终端，支持用户在本地且离线的状态下进行交互式的查看，同时也支持3D模型的导出，比如常见的Gltf、OBJ格式等。而Web端则只支持用户上传已拍摄好的场景图片或视频，只能在网页端查看Mesh模型和固定视角的渲染图像，不支持新视角渲染和3D模型（Mesh和点云）导出。
Luma AI 的unreal engine 5的插件下载插件可以直接使用，免费，无需申请。

基于Nerf的Luma把真实场景搬进虚幻引擎 UE5

Nerf其他应用：

1、Nerf现进已知最大的应用在城市模型、GIS地理信息、CIM、地图上的三维重建，逆渲染方面；
2、NeRF跟其他3D场景表征一样，也被应用于对人体进行建模应用在数字人的脸部建模、人体建模、手部建模，比较千人千面，元宇宙的实现必须要攻克现有的设计师设计或者只能简单得掐掐脸；
3、NeRF作为一种隐式表示，为传统的图像处理方法提供了一种新思路，即从隐式神经表示，或者神经场的角度来处理图像。对图像处理提供了新的思路其中包括：压缩、去噪、超分、inpainting等。同理跟图片的处理一样，视频处理将输入视频分解并“展开”为一组分层2D地图集的方法，每个地图集都提供了视频上对象（或背景）外观的统一表示。
4、处理人脸、手外还是元宇宙的场景，Nerf能快速的把现实中的场景搬到虚拟世界中，虽然这个过程距离现在还有一些长，比如精密，LOD、材质、Mesh可编辑等等，但是这个在未来是很重要的一大方向。