十三届蓝桥杯国赛2022

news2024/11/25 2:35:15

会得噶

    • A 2022
    • B 钟表
    • C 卡牌
    • D 最大数字dfs
    • F 费用报销（不是根据收据个数，而是根据日期dp)
    • H 机房（最近公共祖先lca）
    • I 齿轮
    • J 搬砖（贪心+01背包）

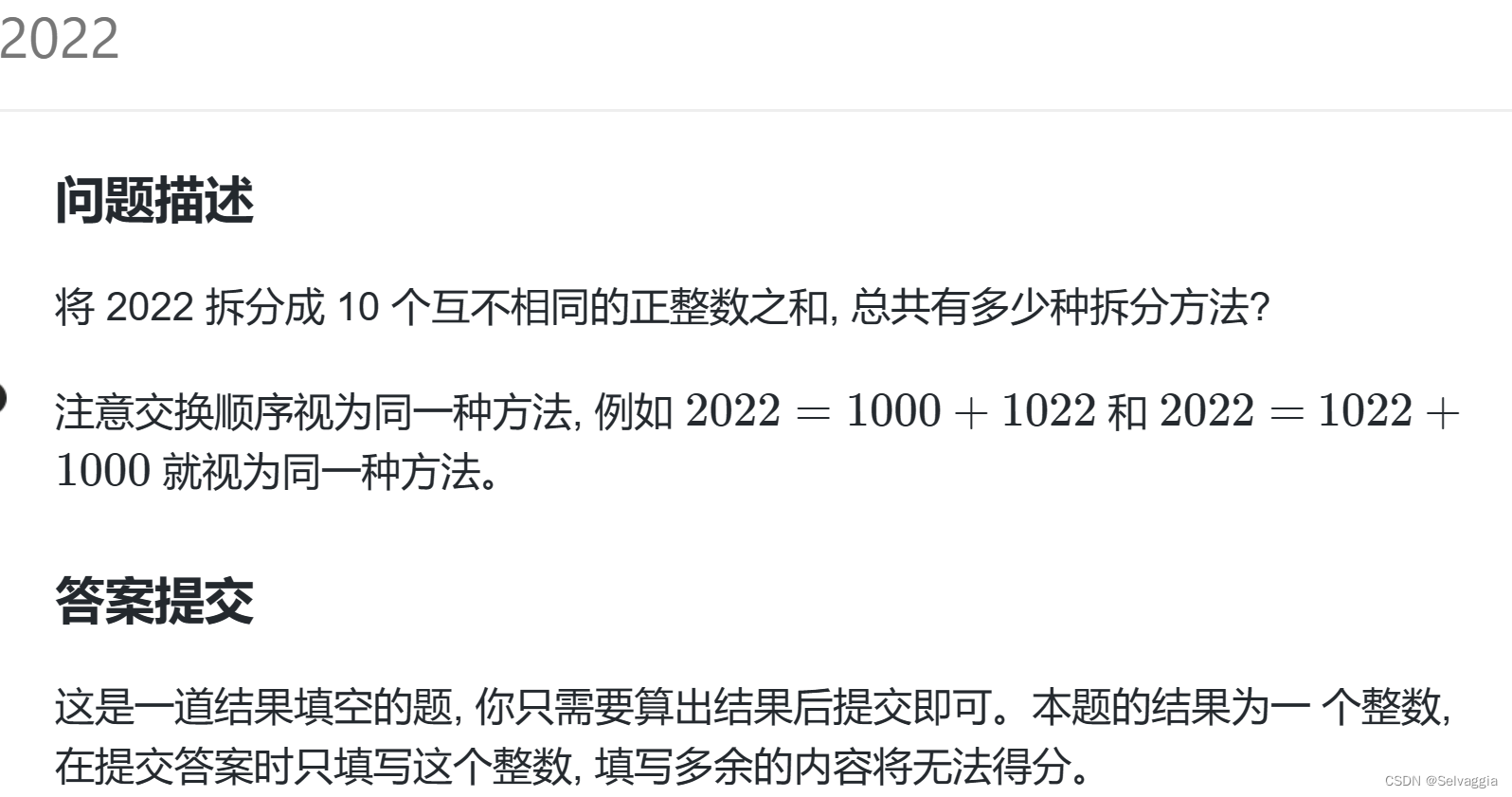
A 2022

在这里插入图片描述

#include <bits/stdc++.h>
using namespace std;
int n,k,x,T;
double pi=acos(-1);
const int N=1e5+5;
int res;
void dfs(int sum,int cnt,int start){
//	cout<<"hhh"<<endl;
	if(sum>2022)return ;
	if(cnt==10){
		if(sum==2022)res++;
		return ;
	}
	if(cnt>10)return ;
	
	for(int i=start;sum+i<=2022;i++){
		dfs(sum+i,cnt+1,i+1);
	}
	
}
signed main(){//10:44
	dfs(0,0,1);
	cout<<res;
    return 0;
}

在这里插入图片描述

#include <bits/stdc++.h>
using namespace std;
#define int long long int
const int N=2023;
int n,k,x,T;
int dp[N][15];//dp[2022][10]
int res;

signed main(){//10:44
	dp[0][0]=1;
	for(int i=1;i<=2022;i++){
		for(int j=0;j<=10;j++){
			if(i>=j)dp[i][j]=dp[i-j][j]+dp[i-j][j-1];
//将i分成j个数 == 将 i-j 分给j个数(每个数多分1) + 将 i-j 分给j-1个数(将j单独分成一个数)

		}
	}
	cout<<dp[2022][10];
    return 0;
}

分苹果，不同之处在于一个盘子可以放0个苹果

B 钟表

在这里插入图片描述

#include <bits/stdc++.h>
using namespace std;
#define int long long int
const int N=2023;
int n,k,x,T;

signed main(){//10:44
//	int s,f,m;
	for(double i=0;i<=6;i++){//时
		for(double j=0;j<=60;j++){//分
			for(double k=0;k<=60;k++){//秒
				double c=360/60*k;
				double b=360/60*(j+k/60);//分针，一分钟
				double a=360/12*(i+(j*60+k)/3600);
				double A=abs(a-b);
				double B=abs(c-b);
				A=min(360-A,A);
				B=min(360-B,B);
				if(abs(A-B*2)<=0.001){
					cout<<i<<" "<<j<<" "<<k<<endl;
				}
			}
		}
	}
    return 0;
}

0 0 0
4 47 60
4 48 0

C 卡牌

在这里插入图片描述

#include <bits/stdc++.h>
using namespace std;
#define int long long int
const int N=2e5+5;
int n,m,k,x,T;
int a[N];
int b[N];
bool adequate(int x){
	int cnt=0;
	for(int i=1;i<=n;i++){
		if(a[i]<x){
			if(a[i]+b[i]<x)return false;
			cnt+=(x-a[i]);
			if(cnt>m)return false;
		}
		
	}
	return true;
}
signed main(){
	cin>>n>>m;
	int mx=0x3f3f3f3f;
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int i=1;i<=n;i++)cin>>b[i],mx=min(mx,a[i]+b[i]);
	//求最小值而不是最大值，最短板限制了套数
	int l=0,r=mx;
	while(l<r){
		int mid=(l+r+1)>>1;
		if(adequate(mid)){
			l=mid;
		}
		else r=mid-1;
	}
	cout<<l;
    return 0;
}

直接贪心思想

#include <bits/stdc++.h>
using namespace std;
#define int long long int
#define pii pair<int,int>
const int N=2e5+5;
int n,m,k,x,T;
int a[N];
int b[N];

signed main(){
	cin>>n>>m;
	priority_queue<pii,vector<pii>,greater<pii> > Q;
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int i=1;i<=n;i++)cin>>b[i],Q.push({a[i],b[i]});
	//最短板限制了套数，贪心思想就是每次补最少的牌
	while(m--){
		pii t=Q.top();Q.pop();
		if(t.second==0)break;
		t.first++;
		t.second--;
		Q.push(t);
	}
	cout<<Q.top().first;
    return 0;
}

D 最大数字dfs

在这里插入图片描述
在这里插入图片描述

#include <bits/stdc++.h>
using namespace std;
#define int long long int
#define pii pair<int,int>
const int N=25;
int n,m,k,x,T,a,b;
vector<int> v;
signed main(){
	cin>>n>>a>>b;
	
	while(n){
		int x=n%10;
		n/=10;
		v.push_back(x);
	}
	reverse(v.begin(),v.end());
	int cnt=v.size();
	for(int i=0;i<cnt;i++){
		int s=v[i];
		int x=s-(-1);
		int y=9-s;
		if(x<=b&&y<=a){
			if(y<x){
				a-=y,v[i]=9;
			}
			else{//尽量保留a的次数
				b-=x,v[i]=9;		
			}
		}
		else if(y<=a){
			a-=y,v[i]=9;
		}
		else if(x<=b){
			b-=x,v[i]=9;
		}
		else{
			v[i]+=a,a=0;
		}
		cout<<v[i];
	}
    return 0;
}

过了90%，这种贪心其实无法保证全局最优
哪个局部没有最优呢？if(x<=b&&y<=a)这里，是选则用A还是用B
我的选取规则是 尽量保留AB的总次数尤其是A，我想的是在AB都无法到达9的时候，只能用上A。但是，B也很珍贵，比如B为3 ，A为8， N为219999，非常显然在2上用A不用B，尽管2-(-1)<9-2

还是得dfs搜索选取方法，但可以进行适当的剪枝，因为B操作是可以判断当下是否选取的。注意的点是对于 AB操作的次数，可以把ａｂ当作dfs的参数，如果不，那就得记得还原现场

#include <bits/stdc++.h>
using namespace std;
#define int long long int
#define pii pair<int,int>
const int N=25;
int n,m,k,x,T,a,b;
vector<int> v;
int cnt;
int res=0;
void dfs(int u,int sum){
	if(u==cnt){
		res=max(res,sum);
		return ;
	}
	int x=v[u];
//	对于元素v[u]使用A操作
	int op=min(a,9-x);
	a-=op;
	dfs(u+1,sum*10+x+op);
	a+=op;//还原现场，考虑是否对于元素v[u]使用B操作
	if(b>=x-(-1)){
		b-=(x-(-1));
		dfs(u+1,sum*10+9);
		b+=(x-(-1));
	}
	
}
signed main(){
	cin>>n>>a>>b;
	
	while(n){
		int x=n%10;
		n/=10;
		v.push_back(x);
	}
	reverse(v.begin(),v.end());
	cnt=v.size();
	dfs(0,0);
	cout<<res;
    return 0;
}

如果不剪枝，极其暴力枚举所有方式，就可以通过得到二进制数集合

void dfs(int u){
	if(u==cnt){
		for(int i=0;i<cnt;i++){
			if(op[i]==1){//A操作
				
			}
			else{//B操作
				
			}
		}
	}
	op[u]=0;
	dfs(u+1);
	op[u]=1;
	dfs(u+1);
}
dfs(0);

F 费用报销（不是根据收据个数，而是根据日期dp)

在这里插入图片描述

4 16 3
1 1 1
1 3 2
1 4 4
1 6 8

在这里插入图片描述

简洁版

#include <bits/stdc++.h>
using namespace std;
#define int long long int
#define pii pair<int,int>
const int N=366;
int n,m,k,x,d,a,b,to;
int v[N];
int dp[N];//第i天之前的所有收据可以取得的最大金额
int month[15]={0,31,28,31,30,31,30,31,31,30,31,30,31};
int date(int m,int d){
	int ans=0;
	for(int i=1;i<m;i++){
		ans+=month[i];
	}
	ans+=d;
	return ans;
}
signed main(){
	cin>>n>>to>>k;
	for(int i=0;i<n;i++){
		cin>>m>>d>>x;
		v[date(m,d)]=max(v[date(m,d)],x);//一定要避免大的被小的覆盖掉
	}
//	因为要满足相距k天的条件，一个一个收据来不行，要根据日期来选择
	dp[0]=v[0];
	for(int i=1;i<=365;i++){
		dp[i]=dp[i-1];//每一步都保证满足条件，所以dp[i-1]一定满足
		if(i>=k&&dp[i-k]+v[i]<=to)dp[i]=max(dp[i-k]+v[i],dp[i]);//取，不取
		else if(v[i]<=to)dp[i]=max(v[i],dp[i]);
	}
	cout<<dp[365];
    return 0;
}
//4 16 3
//1 1 1
//1 3 2
//1 4 4
//1 6 8

推导版

#include <bits/stdc++.h>
using namespace std;
#define int long long int
#define pii pair<int,int>
const int N=366;
int n,m,k,x,d,a,b,to;
//vector<pii> v;
int v[N];
//map<int,int> v;
int cnt;
int res=0;
int dp[N];//第i天之前的所有收据可以取得的最大金额
int month[15]={0,31,28,31,30,31,30,31,31,30,31,30,31};
int date(int m,int d){
	int ans=0;
	for(int i=1;i<m;i++){
		ans+=month[i];
	}
	ans+=d;
	return ans;
}
signed main(){
	cin>>n>>to>>k;
	for(int i=0;i<n;i++){
		cin>>m>>d>>x;
//		v.push({date(m,d),x});
//		v[date(m,d)]=x;
		v[date(m,d)]=max(v[date(m,d)],x);//一定要避免大的被小的覆盖掉
	}
//	sort(v.begin(),v.end());
//	int mx=v[v.size()-1].first;
//	int l=0;不是双指针
	for(int i=0;i<n;i++){//对于前i个收据，能取得的最大价值
//		for(int j=0;j<=mx;j++){
//			dp[i][j]+=dp[i-1][j-k]
//		}
	}
//	因为要满足相距k天的条件，一个一个收据来不行，要根据日期来选择
	dp[0]=v[0];
	for(int i=1;i<=365;i++){
//		if(i>=k)
//		dp[i]=dp[i-k]+v[i];//考虑相距k天
//		if(i>=k)dp[i]=max(dp[i-k]+v[i],dp[i-1]);//取，不取
//		else dp[i]=max(v[i],dp[i-1]);
//还要考虑不超过m
		dp[i]=dp[i-1];//每一步都保证满足条件，所以dp[i-1]一定满足
		//上为不取，下位取，取有两种，如果k天前的可以取
		if(i>=k&&dp[i-k]+v[i]<=to)dp[i]=max(dp[i-k]+v[i],dp[i]);//取，不取
		else if(v[i]<=to)dp[i]=max(v[i],dp[i]);//不要忘了这条，取有两种
	}
	cout<<dp[365];
    return 0;
}
//4 16 3
//1 1 1
//1 3 2
//1 4 4
//1 6 8

H 机房（最近公共祖先lca）

在这里插入图片描述

4 3
1 2
1 3
2 4
2 3
3 4
3 3

在这里插入图片描述
正是因为树有着“不包含回路”这个特点，所以树就被赋予了很多特性。
1、一棵树中的任意两个结点有且仅有唯一的一条路径连通。
2、一棵树如果有n个结点，那么它一定恰好有n-1条边。
在这里插入图片描述

#include <bits/stdc++.h>
using namespace std;
#define int long long int
#define pii pair<int,int>
const int N=2e5+5;
int n,m,k,x,y;
vector<int> v[N];//存放邻接边
//思路：要求解任意两个节点 一路上所经历的所有节点的延迟总和
//注意n个节点n-1条边一定是树，树中任意两个结点之间的路径是唯一的
//那么很显然，就是到达公共祖先那条路
//多组1e5询问，每次都dfs得到路径上的所有节点可能会超时？可以过！！！
//当然也可以用前缀和的思想

int dep[N],fa[N];//存放每个节点的深度，为寻找公共祖先lca做准备
int pos[N];//每个节点，从根节点到该节点一路上节点的推迟总数，类似前缀和
void dfs(int u,int father){
	fa[u]=father;
	for(int i=0;i<v[u].size();i++){
		int to=v[u][i];
		if(to==father)continue ;
		dep[to]=dep[u]+1;
		pos[to]=pos[u]+v[to].size();//前缀和
		dfs(to,u);
	}	
}
int lca(int u,int v){//对于任意两个节点，先使他们处在同一深度，再往上
	if(dep[u]<dep[v])swap(u,v);
	while(dep[u]!=dep[v]){
		u=fa[u];
	}
//	while(fa[u]!=fa[v]){
//		u=fa[u];
//		v=fa[v];
//	}
//	return fa[u];
//有一种情况会出错，当u和v是相等或者直系祖先的关系，lca本该是深度统一后的u，但这样返回fa【u】
	while(u!=v){
		u=fa[u];
		v=fa[v];
	}
	return u;
}
signed main(){
	scanf("%d %d",&n,&m);
	for(int i=0;i<n-1;i++){
		scanf("%d %d",&x,&y);
		v[x].push_back(y);
		v[y].push_back(x);
	}
	dep[1]=1;pos[1]=v[1].size();//postpone
	
	dfs(1,0);
	while(m--){
		scanf("%d %d",&x,&y);
		cout<<pos[x]+pos[y]-2*pos[lca(x,y)]+v[lca(x,y)].size()<<endl;
	}
    return 0;
}


#include <bits/stdc++.h>
using namespace std;
#define int long long int
#define pii pair<int,int>
const int N=2e5+5;
int n,m,k,x,y;
vector<int> v[N];//存放邻接边
//思路：要求解任意两个节点 一路上所经历的所有节点的延迟总和
//注意n个节点n-1条边一定是树，树中任意两个结点之间的路径是唯一的
//那么很显然，就是到达公共祖先那条路
//多组1e5询问，每次都dfs得到路径上的所有节点不太可行？

int dep[N],fa[N];//存放每个节点的深度，为寻找公共祖先lca做准备
int pos[N];//每个节点，从根节点到该节点一路上节点的推迟总数，类似前缀和
void dfs(int u,int father){
	fa[u]=father;
	for(int i=0;i<v[u].size();i++){
		int to=v[u][i];
		if(to==father)continue ;
		dep[to]=dep[u]+1;
		pos[to]=pos[u]+v[to].size();//前缀和
		dfs(to,u);
	}	
}

int Lca(int u,int vv){//对于任意两个节点，先使他们处在同一深度，再往上
	int res=0;
	if(dep[u]<dep[vv])swap(u,vv);
	while(dep[u]!=dep[vv]){
		res+=v[u].size();
		u=fa[u];
		
	}
//	res+=v[u].size();
	if(u==vv)return res+v[u].size();
	while(u!=vv){
		res+=v[u].size();
		res+=v[vv].size();
		u=fa[u];
		vv=fa[vv];
	}
	res+=v[u].size();
	return res;
}
signed main(){
	scanf("%d %d",&n,&m);
	for(int i=0;i<n-1;i++){
		scanf("%d %d",&x,&y);
		v[x].push_back(y);
		v[y].push_back(x);
	}
	dep[1]=1;pos[1]=v[1].size();//postpone
	
	dfs(1,0);
	while(m--){
		scanf("%d %d",&x,&y);
//		cout<<pos[x]+pos[y]-2*pos[lca(x,y)]+v[lca(x,y)].size()<<endl;
cout<<Lca(x,y)<<endl;
	}
    return 0;
}
//4 3
//1 2
//1 3
//2 4
//2 3
//3 4
//3 3

I 齿轮

在这里插入图片描述
在这里插入图片描述

要么单独判断是否有一对数是一倍的关系，要么mp记录a【i】出现的次数，如果是一倍且只出现过一次，不计入ans

错误

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int,int>
const int N=2e5+5;
int n,m,k,x,T,b,q;
int a[N];
int cnt;
int res;//最右边的是最左边的多少倍，右边是左边的多少倍a[i-1]/a[i]
//map<int,int> mp;
int mp[N],ans[N];//容器可能会慢
signed main(){
	scanf("%d %d",&n,&q);
	for(int i=0;i<n;i++)cin>>a[i],mp[a[i]]=1;
//  for(int i=1;i<n;i++){
//	   res=res*(a[i-1]/a[i]);//可以相约，其实就是a[0]/a[n-1]
//}	
//其实就是看n个数中，是否存在两个数，一个数是另一个数的k倍
//由于k的值是多组输入，
	sort(a,a+n);
	for(int i=0;i<n;i++){
		if(i>0&&a[i]==a[i-1])continue;
		int x=a[i];
		for(int j=x;j<=a[n-1];j+=x){
			
			if(mp[j])ans[j/x]=1;
		}
	}
	while(q--){
		scanf("%d",&k);
		if(ans[k])cout<<"YES";
		else cout<<"NO";
		cout<<endl;
	}
    return 0;
}


//if(res==倍数)
//有没有一对数比值为res
//res<1取倒数，使得res>=1
//排序

正确

#include <bits/stdc++.h>
using namespace std;
#define int long long int
#define pii pair<int,int>
const int N=2e5+5;
int n,m,k,x,T,b,flag,q;
int a[N];
int cnt;
int res;//最右边的是最左边的多少倍，右边是左边的多少倍a[i-1]/a[i]
//map<int,int> mp;
int mp[N],ans[N];//容器可能会慢
signed main(){
	scanf("%d %d",&n,&q);
	for(int i=0;i<n;i++){
		cin>>a[i];
		if(mp[a[i]])flag=1;
		mp[a[i]]=1;
	}
	if(flag)ans[1]=1;
//  for(int i=1;i<n;i++){
//	   res=res*(a[i-1]/a[i]);//可以相约，其实就是a[0]/a[n-1]
//}	
//其实就是看n个数中，是否存在两个数，一个数是另一个数的k倍
//由于k的值是多组输入，
	sort(a,a+n);
	for(int i=0;i<n;i++){
		if(i>0&&a[i]==a[i-1])continue;
		int x=a[i];
		for(int j=x*2;j<=a[n-1];j+=x){
			
			if(mp[j])ans[j/x]=1;
		}
	}
	//不理解这个测试样例
  if(n==1 && a[0] == 123){
        cout<<"YES"<<endl<<"NO"<<endl;  return 0; 
  }
	while(q--){
		scanf("%d",&k);
		if(ans[k])cout<<"YES";
		else cout<<"NO";
		cout<<endl;
	}
    return 0;
}


//if(res==倍数)
//有没有一对数比值为res
//res<1取倒数，使得res>=1
//排序

J 搬砖（贪心+01背包）

在这里插入图片描述
在这里插入图片描述

5
4 4
1 1
5 2
5 5
4 3

大佬思路
在这里插入图片描述
我想，单单考虑任意两块砖的摆放位置，就是一种局部的贪心最优思想，大胆推测局部最优导致最优！
深刻领会01背包了吗

#include <bits/stdc++.h>
using namespace std;
#define int long long int
#define pii pair<int,int>
const int N=1005;
const int M=2e4+5;
int n;
//int w[N];
//int v[N];
struct node{
	int w,v;
	bool operator<(const node& p)const{
		return w+v<p.w+p.v;
	}
}a[N];
int dp[M];
signed main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
//		cin>>w[i]
		scanf("%d %d",&a[i].w,&a[i].v);
	}
	sort(a+1,a+n+1);
一定是质量轻的尽可能放在上面，同样质量的，价值大的在上
//dp[i][j];//前i个 质量为j的价值
//if(j<=v[i])dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
	for(int i=1;i<=n;i++){
		for(int j=a[i].w+a[i].v;j>=a[i].w;j--){//前i个物品的最大质量是 w[i]+v[i]
			dp[j]=max(dp[j],dp[j-a[i].w]+a[i].v);
		}
	}
	
//	cout<<dp[n][m];
	int res=0;
	for(int j=0;j<=M;j++)res=max(res,dp[j]);//不知道n件物品中被选择的总重量
	cout<<res;
    return 0;
}
//for(int i=0;i<n;i++){
//	for(int j=0;j<=m;j++){
//		dp[i][j]=dp[i-1][j];
//		if(j>=w[i])dp[i][j]=max(dp[i][j],dp[i-1][j-w[i]]+v[i]);
//	}
//}
//for(int i=0;i<n;i++){
//	for(int j=m;j>=w[i];j--){
//		dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
//	}
//}
//dp[i][j] 选了前i个物品，总重量为j时能获得的最大价值

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/599324.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Openlayers如何设置米作为作为圆形的真实半径，解决圆形半径跟随地图缩放同时缩放的失真问题

Openlayers如何设置米作为作为圆形的真实半径，解决圆形半径跟随地图缩放同时缩放的失真问题

专栏目录： OpenLayers入门教程汇总目录 前言 相信找到这篇文章的同学肯定遇到了Openlayers直接设置圆形半径（ radius）单位不准确的问题，而且失真严重。这是因为默认圆形半径设置的是浏览器像素大小，而不是真实地理信息中的半径长度。那么怎么进行转换成我们现实中的“米…
阅读更多...
python+vue校园快递代取系统的设计与实现3i0v9

python+vue校园快递代取系统的设计与实现3i0v9

开发语言&#xff1a;Python 框架&#xff1a;django/flask Python版本&#xff1a;python3.7.7 数据库&#xff1a;mysql 数据库工具&#xff1a;Navicat 开发软件&#xff1a;PyCharm 本系统名为“基于vue快递代取系统”&#xff0c;系统主要适用于毕业设计&#xff0c;不…
阅读更多...
【数据分享】1929-2022年全球站点的逐日最高气温（Shp\Excel\12000个站点）

【数据分享】1929-2022年全球站点的逐日最高气温（Shp\Excel\12000个站点）

气象数据是在各项研究中都经常使用的数据&#xff0c;气象指标包括气温、风速、降水、湿度等指标&#xff0c;其中又以气温指标最为常用&#xff01;说到气温数据&#xff0c;最详细的气温数据是具体到气象监测站点的气温数据&#xff01; 之前我们分享过1929-2022年全球气象站…
阅读更多...
高通滤波学习(opencv)

高通滤波学习(opencv)

以下代码参考视频解析 这段代码使用了二维FFT变换对输入图像进行频域处理&#xff0c;并设计了一个简单的高通滤波器。 前两行使用了numpy库中的fft2函数对输入图像image进行二维傅里叶变换&#xff08;FFT&#xff09;。接着&#xff0c;fft_shift函数将转化后的频谱数据fft…
阅读更多...
什么是DOM和BOM？

什么是DOM和BOM？

一、什么是DOM DOM 全称是 Document Object Model&#xff0c;也就是文档对象模型。提供操作页面元素的方法和属性&#xff0c;是HTML和XML的API&#xff0c;DOM把整个页面规划成由节点层级构成的文档。 DOM 树 DOM树是Web页面的模型&#xff0c;当浏览器加载一个Web页面时&am…
阅读更多...
A Framework for Evaluating Gradient Leakage Attacks in Federated Learning

A Framework for Evaluating Gradient Leakage Attacks in Federated Learning

联邦学习中梯度泄漏攻击评估框架 摘要&#xff1a; 针对问题&#xff1a;从客户端向联邦服务器共享本地参数更新也可能容易受到梯度泄漏攻击&#xff0c;并侵犯客户端关于其训练数据的隐私。 提出了一个原则性框架&#xff0c;用于评估和比较不同形式的客户端隐私泄露攻击。…
阅读更多...
路径规划算法：基于纵横交叉优化的路径规划算法- 附代码

路径规划算法：基于纵横交叉优化的路径规划算法- 附代码

路径规划算法&#xff1a;基于纵横交叉优化的路径规划算法- 附代码 文章目录 路径规划算法&#xff1a;基于纵横交叉优化的路径规划算法- 附代码1.算法原理1.1 环境设定1.2 约束条件1.3 适应度函数 2.算法结果3.MATLAB代码4.参考文献 摘要&#xff1a;本文主要介绍利用智能优化…
阅读更多...
Eclipse导入项目的配置步骤说明

Eclipse导入项目的配置步骤说明

1.数据库创建并导入 &#xff08;1&#xff09;打开navicat&#xff0c;右击&#xff0c;选择创建数据库&#xff0c;进入新建数据库页面&#xff0c;输入数据库名称。我这里创建的是report数据库。 &#xff08;2&#xff09;右击自己创建的数据库&#xff0c;选择运行sql文件…
阅读更多...
【C++】STL——stack OJ练习

【C++】STL——stack OJ练习

文章目录 1. 最小栈思路分析AC代码拓展思维 2. 栈的压入、弹出序列思路讲解AC代码 3. 逆波兰表达式求值思路讲解AC代码拓展&#xff1a;中缀表达式如何转后缀 这篇文章我们来做几道stack相关的OJ题&#xff0c;练习一下stack的使用。 1. 最小栈 先来看第一道题——&#xff1a…
阅读更多...
【人工智能】常见问题以及解答

【人工智能】常见问题以及解答

1 什么是人工智能 人工智能&#xff08;Artificial Intelligence, AI&#xff09;是一门涉及计算机科学、数学、心理学、哲学等多个领域的交叉学科&#xff0c;旨在研究如何使计算机能够像人一样地思考、学习和行动。 在过去几十年中&#xff0c;人工智能技术得到了广泛的应用…
阅读更多...
LNMP部署

LNMP部署

LNMP部署 一、安装Nginx服务二、安装mysql服务三、安装配置PHP解析环境四、部署 Discuz&#xff01;社区论坛 Web 应用五、fpm参数优化 LNMP架构&#xff1a; LNMP代表的就是&#xff1a;Linux系统下NginxMySQLPHP这种网站服务器架构Linux是一类Unix计算机操作系统的统称&#…
阅读更多...
【P47】JMeter JSON断言（JSON Assertion）

【P47】JMeter JSON断言（JSON Assertion）

文章目录 一、JSON断言&#xff08;JSON Assertion&#xff09;参数说明二、准备工作三、测试计划设计3.1、Assert JSON Path exists3.2、Additionally assert value3.3、Expect null3.4、Invert assertion &#xff08;will fail if above conditions met&#xff09; 一、JSO…
阅读更多...
双链表、循环链表、静态链表

双链表、循环链表、静态链表

目录 一、双链表1、为什么要引入双链表2、双链表的插入操作3、双链表的插入操作 二、循环链表1、循环单链表2、循环双链表 三、静态链表 一、双链表 1、为什么要引入双链表 单链表结点中只有一个指向其后继的指针&#xff0c;使得单链表只能从头结点依次顺序地向后遍历。要访…
阅读更多...
数据治理核心保障数据质量监控开源项目Apache Griffin分享

数据治理核心保障数据质量监控开源项目Apache Griffin分享

文章目录 概述定义为何要做数据质量监控基本概念特性架构 安装Docker部署Docker 镜像批处理使用Docker 镜像流处理使用UI界面操作 概述 定义 Apache Griffin 官网地址 https://griffin.apache.org/ 源码release最新版本0.6.0 Apache Griffin 官网文档地址 https://griffin.apa…
阅读更多...
MySQL学习（联结，组合查询，全文本搜索）

MySQL学习（联结，组合查询，全文本搜索）

联结 SQL最强大的功能之一就是能在数据检索查询的执行中联结表&#xff1b; 关系表 为什么要使用关系表&#xff1f; 使用关系表可以储存数据不重复&#xff0c;从而不浪费时间和空间&#xff1b;如果有数据信息变动&#xff0c;只需更新一个表中的单个记录&#xff0c;相关…
阅读更多...
研发工程师玩转Kubernetes——Node失效后的Pod的调度实验

研发工程师玩转Kubernetes——Node失效后的Pod的调度实验

在《研发工程师玩转Kubernetes——多Worker Node部署》中&#xff0c;我们创建了Master Node: UbunutA&#xff0c;以及四个Worker Node:UbunutB、UbunutC、UbunutD和UbunutE。本节我们将使用Deployment创建只含有一个nginx的Pod&#xff0c;然后关掉它所在的主机以模拟Node失效…
阅读更多...
使用Adobe Acrobat DC对.jpg和.png格式图片转换为.eps图片格式举例

使用Adobe Acrobat DC对.jpg和.png格式图片转换为.eps图片格式举例

使用Adobe Acrobat DC对.jpg和.png等格式图片转换为.eps图片格式举例 在进行有的文档排版编辑时候&#xff08;比如使用winEdt进行排版CTEX文件时候&#xff09;&#xff0c;需要添加.eps格式的图片&#xff0c;然而电脑中的画图&#xff0c;word和ppt等中无法实现.eps格式图片…
阅读更多...
centos7 glib2.0 arm版本的编译

centos7 glib2.0 arm版本的编译

最近在看bluez代码&#xff0c;想编译个例子来玩一下&#xff0c;然后bluez里的例子会用到 libglib-2.0 库里的接口&#xff0c;于是开始了漫长的编译 arm 版本的 libglib-2.0&#xff0c;Linux 系统有时就是很麻烦&#xff0c;要编译一个库&#xff0c;结果发现依赖一大堆库&a…
阅读更多...
Linux命令学习之帮助命令man

Linux命令学习之帮助命令man

cat /proc/version和uname -a可以查看CentOS内核使用版本。 我使用的Linux操作系统发行版本号是7.6.1810&#xff0c;可以通过cat /etc/redhat-release进行查看。 man man是manual的缩写&#xff0c;是操作说明的意思。 使用man touch想要看一下touch的使用帮助&#xff0c;…
阅读更多...
OpenMMLab开营笔记

OpenMMLab开营笔记

摘要 很高兴能加入OpenMMLab AI实战营&#xff0c;成为第二期4班的一名学员。OpenMMLab经过几年的发展和沉淀&#xff0c;其开源项目已经覆盖到计算机视觉的各个领域。OpenMMLab 为香港中文大学-商汤科技联合实验室 MMLab 开源的算法平台&#xff0c;不到两年时间&#xff0c;…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023