一、双链表

1、为什么要引入双链表

单链表结点中只有一个指向其后继的指针，使得单链表只能从头结点依次顺序地向后遍历。要访问某个结点的前驱结点（插入、删除操作时），只能从头开始遍历，访问后继结点的时间复杂度为O(1)，访问前驱结点的时间复杂度为O(n)。

为了克服单链表的上述缺点，引入了双链表，双链表结点中有两个指针prior和next，分别指向其前驱节点和后继结点，双链表结构如下图所示：

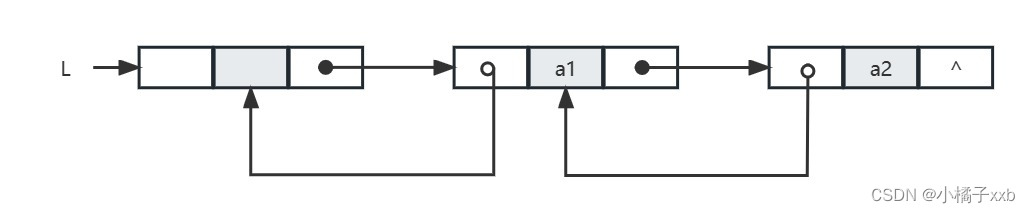
双链表中结点类型的描述如下：

typedef struct DNode{
	ElemType data;//数据域
	struct DNode *prior,*next;//前驱和后继指针
}DNode,*DLinklist;

双链表在单链表的结点中增加了一个指向其前驱的prior指针，因此双链表中的按值查找和按位查找的操作与单链表的相同，但双链表在插入和删除操作的实现上，与单链表有着较大的不同。因为在“链”变化时需要同步对prior指针做出修改，其关键是保证在修改的过程中不断链。双链表中的结点可以很方便的找到其前驱结点，因此，插入、删除操作的时间复杂度仅为O(1)。

2、双链表的插入操作

在双链表中p所指的结点之后插入结点*s，其指针的变化过程如下图所示：

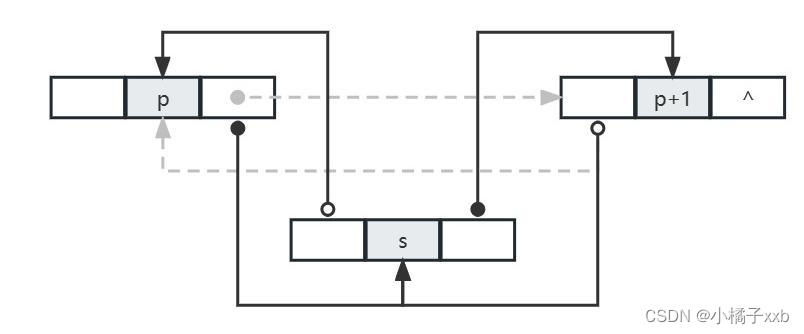
插入操作的代码片段如下：

s->next=p->next;
p=next->prior=s;
s->prior=p;
p->next=s;

注意：必须先处理p+1结点再处理p结点，否则会导致断链。

3、双链表的插入操作

删除双链表中结点p的后继节点q，其指针变化如下图所示：

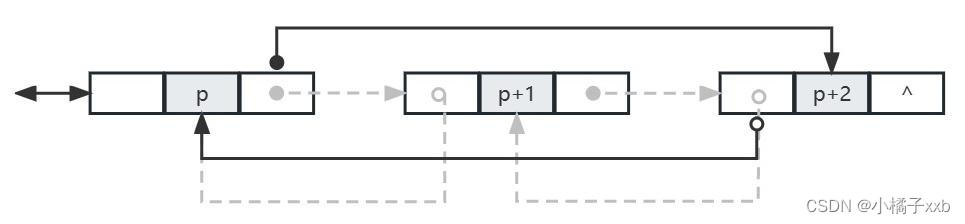
删除操作的代码片段如下：

p->next=(q+1)->next;
(p+1)->next->prior=p;
free(q+1);

二、循环链表

1、循环单链表

循环单链表和单链表的区别在于，表中最后一个结点的指针不是NULL，而改为指向头结点，从而整个链表形成一个环，如下图所示：

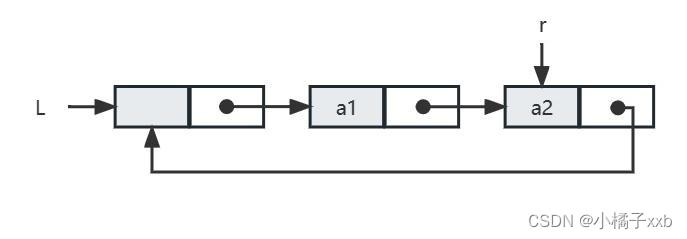
循环单链表的插入、删除算法与单链表的几乎一样，所不同的是若操作是在表尾进行，则执行的操作不同，以让单链表继续保持循环的性质。也正是因为循环单链表是一个环，在任何一个位置上的插入和删除操作都是等价的，无须判断是否为表尾。

在单链表中只能从表头结点开始往后顺序遍历整个链表，而循环单链表可以从表中的任意一个结点开始遍历整个链表。有时对单链表常做的操作是在表头和表尾进行的，此时对循环单链表不设头指针而仅设尾指针，从而使得操作效率更高。因为若设的是头指针，对表尾进行操作需要O(n)的时间复杂度，而若设的是尾指针r，r->next就指向头指针，对表头和表尾进行操作都只需要O(1)的复杂度。

2、循环双链表

由循环单链表与单链表的关系可以推得循环双链表与双链表的关系。在循环双链表中，头结点的prior指针指向表尾结点，循环双链表的结构如下图所示：

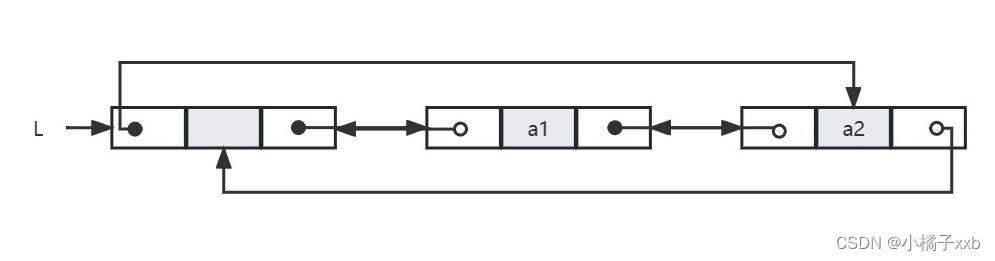
在循环双链表L中，L->next指向p，某节点*p为尾结点时，p->next==L；当循环双链表为空表时，其头结点的piror域和next域都等于L。

三、静态链表

静态链表借助数组来描述线性表的链式存储结构，结点也有数据域data和指针域next，这里的指针是结点的相对地址（数组下标），又称游标。和顺序表一样，静态链表也要预先分配一块连续的内存空间。静态链表示例如下图所示：

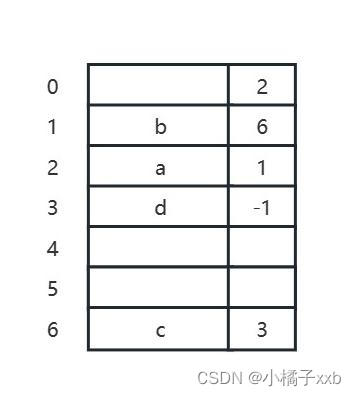
下图为静态链表对应的单链表：

静态链表结构类型的描述如下：

#define MaxSize 50//静态链表的最大长度
typedef struct{
	ElemType data;//存储数据元素
	int next;//下一个元素的数组下标
}

静态链表以next==-1作为其结束的标志。静态链表的插入、删除操作与动态链表的相同，只需要修改指针，而不需要移动元素。总体来说，静态链表没有单链表使用方便，所以其常用于不支持指针的高级语言中，作为单链表的巧妙设计方法。

本文内容为个人学习总结所得，如有错误，欢迎指正。